To Start
我们做题的时候经常会发现一类题型,它们都包含有一种条件——从 \(n\) 个东西中选择 \(k\) 个,然后乌拉乌拉一大堆让你求最优解。
比如 P4767 [IOI2000]邮局 中:
在分布在一条直线上的 \(n\) 个村庄中选 \(k\) 个建立邮局,求所有村庄到达其最近邮局的最小距离之和。\(n\le 3000,k\le 300\).
这是一道四边形不等式优化 dp 的题目,但是四边形不等式好麻烦,我们不想用它 >_<
暴力的 dp 会怎么做它呢?我们通常会设 \(dp_{i,j}\) 表示前 \(i\) 个村庄放 \(j\) 个邮局时的最小距离距离之和,于是有
\[dp_{i,j}=\min(dp_{p,j-1}+w(p+1,i))\ ,\ (0\le p <i) \]其中 \(w(i,j)\) 表示的是在区间 \([i,j]\) 中建立邮局,且该区间内的村庄与该邮局的距离之和。运用一些中位数的知识,显然邮局应该建立在该区间最中间的村庄内。
这样看来 dp 转移是 \(O(n^2 k)\) 的,计算 \(w(i,j)\) 是 \(O(n)\) 的,总复杂度到达了恐怖的 \(O(n^3k)\)。
考虑继续优化,我们发现 \(w(i,j)\) 是可以通过预处理提前求出的,由于一个区间向左右同时扩展一格时中位数不变,所以有递推式:
\[w(i,i)=w(i+1,i)=0\\ w(i,j)=w(i+1,j-1)+a_j-a_i\ ,\ i\le j-1 \]所以我们可以在 \(O(n^2)\) 的复杂度内将 \(w\) 预处理出来,dp 的时间复杂度就优化到了 \(O(n^2k)\)。
但是仍然过不去。考虑继续用四边形不等式优化 拒绝四边形不等式!
我们发现其实 \(n^2\) 完全是能过的,只要我们能将 \(k\) 优化到 \(\log\),他也是能过的。
但是单纯的 dp 显然无法做到,因为选择 \(k\) 个物品这个条件所增加的状态数就足以支撑起 \(O(k)\) 的时间复杂度。
这时就需要用到我们的奇淫技巧——wqs 二分。
Idea
wqs 二分是王钦石在 2012 年的国集论文中提出的,它能够解决的算法模型可以抽象为:
在 \(n\) 个物品中选择其中 \(k\) 个,求最大/小化收益。
如果条件只有这些,那么这个显然可以通过贪心解决。可如果物品的收益并不明晰,无法直接贪心,一般就会用到动态规划。
设 \(dp_{i,j}\) 表示前 \(i\) 个物品中选择 \(j\) 个的最大/小收益,则显然有:
\[dp_{i,j}=\min/\max(dp_{i-1,j},dp_{i-1,j-1}+w_i) \]此时时间复杂度为 \(O(n^2)\),十分不优秀。
而如果我们使用 wqs 二分,则可以将【\(k\) 个】的条件通过二分的复杂度去掉,将原题目等价于 \(n\) 个物品任意取的最大/小收益。这个子问题则可以 \(O(n)\) 解决,即设 \(f(i)\) 为前 \(i\) 个物品的收益,有:
\[f_i=\min/\max(f_{i-1},f_{i-1}+w_i) \]具体怎么实现呢?我们先以求最大收益举例。
设 \(g(i)\) 为 \(n\) 个物品中取 \(i\) 个时的最大收益,由于我们肯定会优先取收益大的物品,所以显然有:
\[g(i)-g(i-1)\ge g(i+1)-g(i) \]即 \(g(i)\) 的函数曲线是上凸的,满足随着 \(i\) 的增大,函数 \(g(i)\) 关于点 \((i,g_i)\) 的切线斜率是单调递减的。大概就像这样:
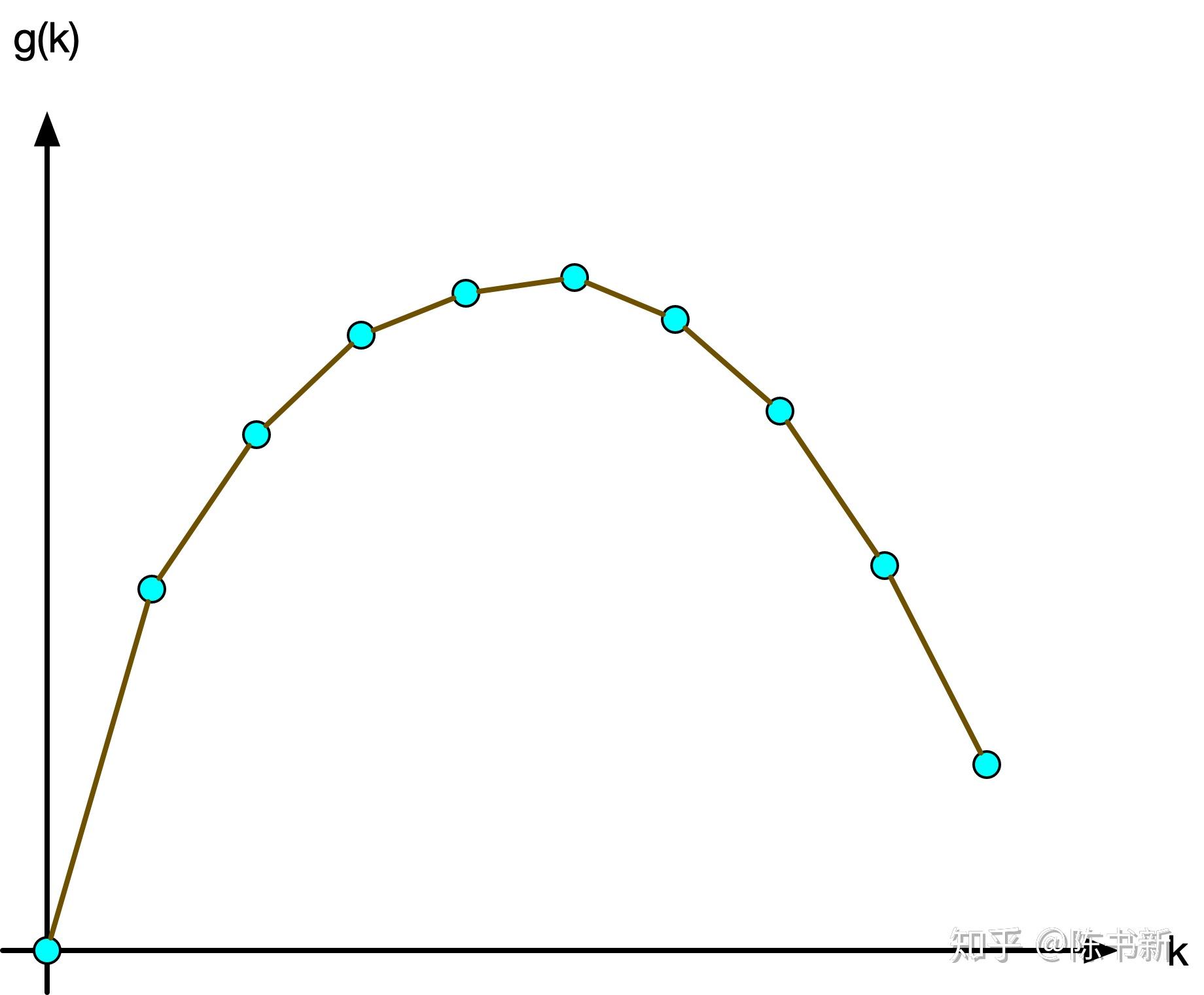
而我们需要求出的就是 \(g(k)\) 的值。
在这样的函数图像上,怎样才能不关注 \(k\) 这个条件得到 \(g(k)\) 呢?
我们发现,上凸壳有一个性质可以帮助我们做到。注意到假设我们枚举直线的斜率,将该直线分别过凸壳上的每一个点,也就是这样:
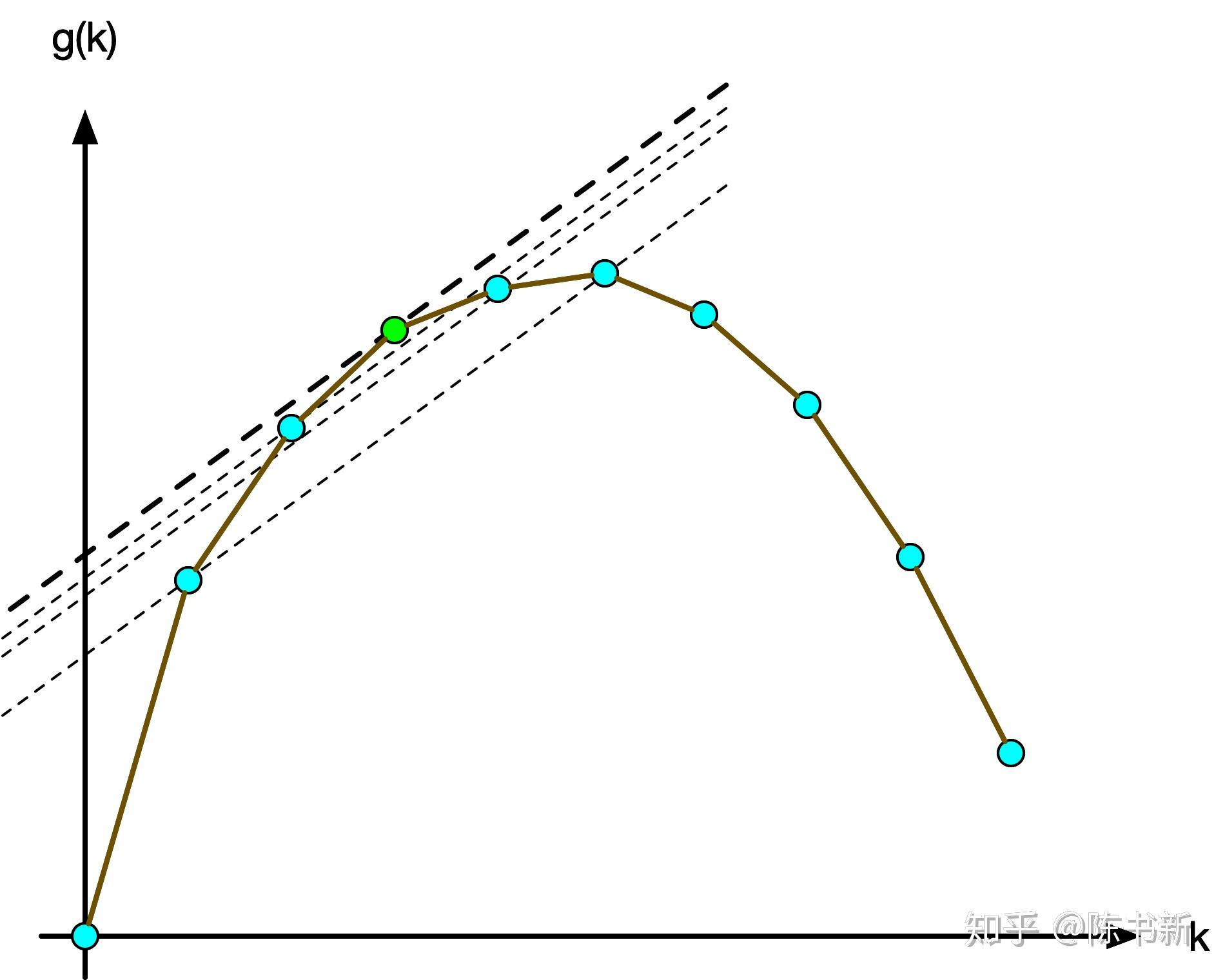
此时与是上凸壳相切的直线的截距一定最大。
我们刚才还说过凸壳有个什么性质来着?随着 \(i\) 的增大,\(g(i)\) 的值是单调递减的。
单调性欸!是不是想到了二分?
考虑二分直线的斜率 \(p\),并将每一个 \(g(i)\) 的值都减去 \(i\times p\),那么每一个 \(g(i)\) 的值都变成了与点 \((i,g_i)\) 相交的、斜率为 \(p\) 的直线的截距 \(s(i)\)。
此时如果跑一遍忽视选择物品个数的 dp,那么选出来的最优方案的物品数 \(i\) 对应的 \(s(i)\) 一定最大。
所以当我们二分到一个斜率时,如果 dp 出来的物品数 \(i<k\) ,则意味着我们需要枚举更小的斜率,需要将右端点 \(r\) 变为 \(mid\) ;否则若 \(i>k\),则需要将左端点 \(l\) 右移为 \(mid\);当 \(i=k\) 时,说明此时的二分到的答案就是 \(s(k)\),将其加上 \(k\times p\) 即为答案 \(g(k)\) 的值。
具象地讲,将 \(g(i)\) 减去 \(i\times p\) 的操作还可以看作是每一个物品贡献减少 \(p\) ,那么显然减少的越多,最优方案下我们愿意选择的物品个数就越少,相反同理。这也侧面证明了函数的凸性质。
不过到这里还并没有结束,因为当存在相同的物品价值的时候,就会存在若干个上凸壳上的点斜率相同,即
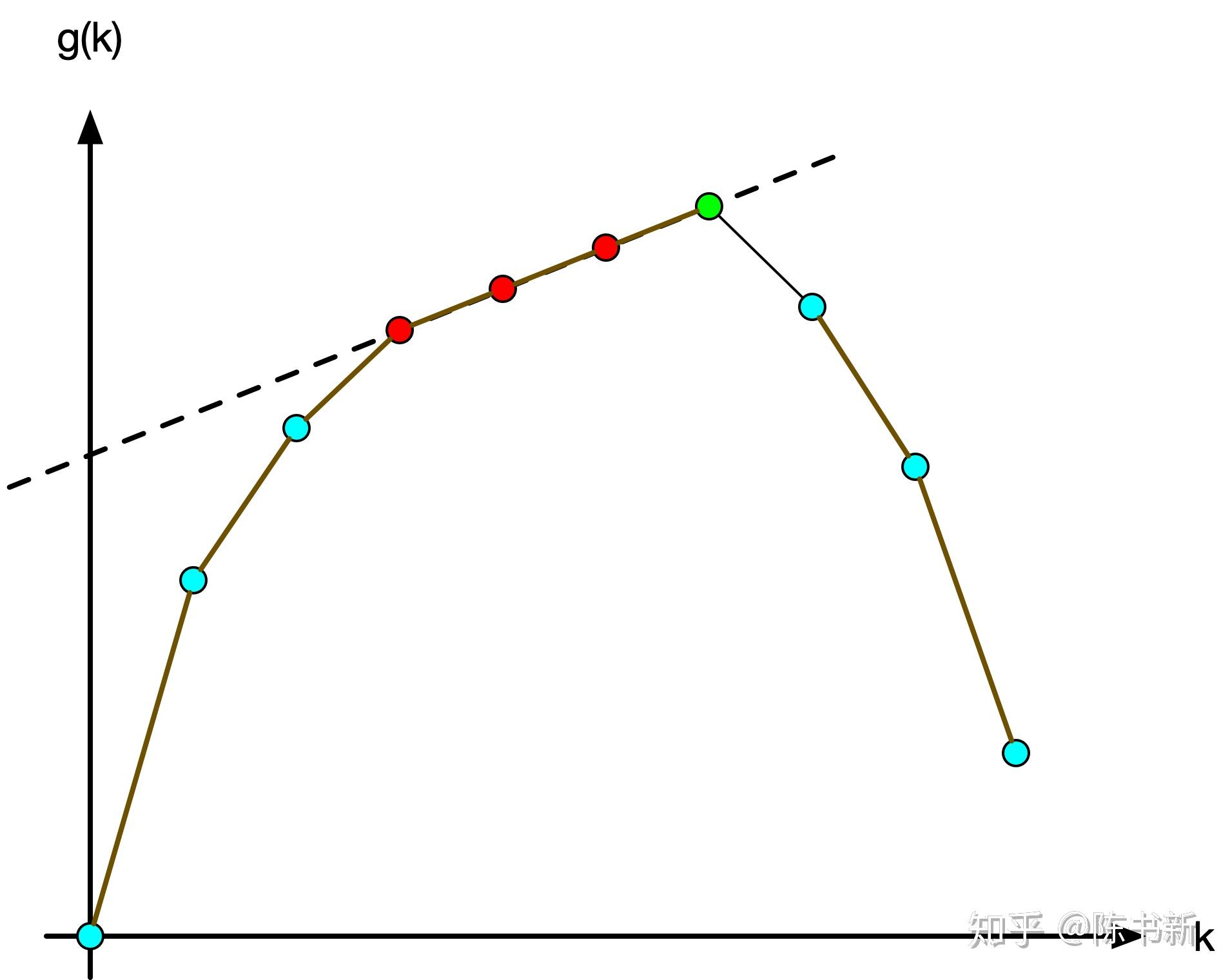
此时当我们找到 \(g(k=5)\) 的斜率时,可能选择了 \(4\) 个物品或者 \(6\) 个物品。
为了使我们的程序在这种情况下依然能够得到正解,我们一般约定尽量多的选择物品,当选择的物品数大于等于 \(k\) 时就更新答案,且由于此时过 \(g(4),g(5),g(6)\) 的直线截距是相同的,所以我们只需要将得到的截距加上 \(k\times p\) 即为答案(注意并非当前斜率得到的物品数乘 \(p\)!)
对于下凸包同理,只不过斜率由单调递减变为了单调递增,交换一下左右端点的更新位置、将找最大截距变为找最小截距即可。
到这里,我们可以简单的总结一下 wqs 二分的基本流程:
- 找到题目中的"\(k\) 个"的条件,发现 \(g(i)\) 的图像是一个凸壳。
- 二分直线斜率,对于每一个斜率用忽略“\(k\) 个”条件的做法解决,并通过该解法选择的物品个数,移动左右端点。若选择的物品个数大于等于 \(k\),则更新答案。
- 最终的答案即为所求。
时间复杂度 \(O(n\log |V|)\)。
wqs 二分在实现时,还有一些点需要注意:
- 注意二分时初始的左右边界,一定要满足是函数图像上需要的斜率范围。
- 尽量多选择物品。例如与决策单调性优化 dp 连用时,一定要注意尽量使用靠后的决策,因为靠后的决策使用的物品个数会更多。
Example
1. P4767 [IOI2000]邮局
接着引入部分的继续往下说。
依旧设 \(g(i)\) 为设立 \(i\) 个邮局时的最小距离之和,则有两个性质:
- \(g(i)<g(i-1)\)
- \(g(i)-g(i-1)\le g(i+1)-g(i)\)
第一条十分显然,每增加一个邮局后的答案显然是不劣,主要看第二条。
第二条其实也很容易想到——每一个邮局造成影响的村庄都一定是一段区间,若后一个邮局的贡献会比前一个优,则前面显然可以先选择后一个邮局的位置建立邮局而非前一个邮局的位置,故贪心的讲,越靠前设立的邮局贡献一定越大。
通过这两条性质,我们可以很容易地推断出 \(g(i)\) 的函数图像是一个下凸壳,于是就可以通过 wqs 二分将邮局个数的限制去掉,再跑 \(O(n^2)\) dp 即可,时间复杂度 \(O(n^2 \log |V|)\),\(|V|\) 是二分的值域。
2. P2619 [国家集训队]Tree I
题目限制了白色边的个数为 \(need\) 条,于是我们可以设 \(g(i)\) 为选择 \(i\) 条白色边的最小的生成树。
设最小生成树方案下选择 \(x\) 条白色边,那显然 \(i\) 和 \(x\) 的差值越大,生成树的权越大。且 \(g(i)\) 同样满足:
\[g(i)-g(i-1)\le g(i+1)-g(i) \]这个性质也很容易证明。考虑初始有一棵全部都为黑色边的生成树,每次将一条黑色边替换为一条白色边,假设第 \(i+1\) 条白色边替换一条黑色边后增加的权值小于第 \(i\) 条,则为了使 \(g(i)\) 更小,我们一定会在选择第 \(i\) 条白色边时先选择原先的第 \(i+1\) 条,则此时 \(g(i)\) 依旧满足上述性质。故得证。
所以 \(g(i)\) 的图像就是一个下凸壳。
于是考虑二分斜率 \(p\),对于每一个斜率将每一条白色边的权值减去 \(p\) 后跑最小生成树,尽量选择白色边,记录当前生成树中白色边的个数与权即可。
时间复杂度 \(O(m\alpha(n)\log |V|)\),\(|V|\) 为二分的值域,\(\alpha(n)\) 为并查集的常数。
Exercise
1. P5308 [COCI2018-2019#4] Akvizna
先考虑朴素的 dp。
设 \(dp_{i,j}\) 表示还剩 \(i\) 个参赛者,进行了 \(j\) 轮比赛之后最多能获得的奖金。
则显然有转移方程:
\[dp_{i,j}=\max(dp_{i,j},dp_{p,j-1}+\frac{p-i}{p}),i< p\le n \]此时时间复杂度为 \(O(n^2k)\),仍需优化。
然后我们发现对于越靠后的决策,分母就越小,当 \(i\) 越来越靠后时,由于分子增长速度相同,故贡献增长越快。由此可以看出,该转移方程的决策具有单调性。
故我们可以采用决策单调性优化 dp,用单调队列动态维护决策,就可以进行 \(O(\log n)\) 转移。时间复杂度为 \(O(nk\log n )\).
但是仍然过不了,还需要优化。观察到题中"恰好 \(k\) 轮"的条件,简单证明凸壳后用 wqs 二分维护即可。
2. CF321E Ciel and Gondolas
出题人就像没有学过语文一样(
下面是简要题意:
将一个长为 \(n\) 的序列分成 \(k\) 段,当 \(i\) 与 \(j\) 被分到一段时会产生 \(u_{i,j}\) 的贡献值,求最小贡献值和。
还是先考虑朴素的 dp。
设 \(dp_{i,j}\) 表示对于序列前 \(i\) 项,分成 \(j\) 段的最小贡献值和。则有转移方程:
\[dp_{i,j}=\min(dp_{i,j},dp_{k,j-1}+w(k+1,i)),1\le k<i \]其中 \(w\) 可以通过二维前缀和 \(O(n^2)\) 预处理,\(O(1)\) 得到。
时间复杂度 \(O(n^2k)\).
又发现对于两个决策 \(p,q\),其中 \(p<q\),那么观察二维贡献矩阵可知,\(p\) 的增长速度是快于 \(q\) 的,即 \(q\) 会随着 \(i\) 的增大而逐渐变得更优。故转移方程满足决策单调性。考虑利用这个性质来优化 dp。用一个单调队列维护决策就可以实现 \(O(\log n)\) 转移。
时间复杂度 \(O(nk\log n)\).
这是大概已经可以过掉本题了,但我们肯定是要精益求精的啦!
观察到 \(k\) 段的限制,证明凸壳后利用 wqs 二分维护即可。
3. CF802O April Fools' Problem (hard)
经典 \(k\) 道题,一眼 wqs 二分。
于是可以抛开这个条件,再来看这道题。
发现我们每次决策的时候可以在打印的时候考虑,打印时考虑打印哪天准备的题目。贪心地来讲,我们一定会选择当前准备+打印总花费最少的题目。
进一步而言,对于每一次打印,我们一定会挑选之前准备花费最少且准备+打印总花费为非正数的题目进行打印。但是这显然还不够。
很显然的反例是,之前准备花费最小的题目在最优情况下,本来应该被后面的打印挑走,却被前面的打印先挑走了。这显然是不行的。
于是考虑反悔,用一个小根堆维护之前的所有决策,每次取出价格最低的决策,将当前打印的花费加上决策花费后,如果总花费为非正数,则先选择该决策。又由于:
\[a_i+b_j-b_j+b_k=a_i+b_j+(-b_j+b_k) \]于是把当前打印的花费的相反数加入堆中,供以后反悔使用即可。
还需要特别注意的一点是,由于 wqs 二分时应尽量多选择物品,所以当正常选的决策和反悔的决策花费相同时,我们应该优先选择正常选的决策,使得物品数更多,防止斜率相同的情况发生而无法处理。
4. P6246 [IOI2000] 邮局 加强版
与普通版邮局类似,加上决策单调性优化即可。
Ending
wqs 二分的应用实际上还是体现了决策与函数之间的关系。
这启发了我们在考虑决策的时候可以尝试将每个决策的答案放在函数图像上,寻找决策之间的性质。
类似的算法还有很多,如斜率优化 dp 等,今后还会逐一总结更新。
标签:二分,邮局,wqs,决策,斜率,物品,奇淫,dp 来源: https://www.cnblogs.com/ydtz/p/16536706.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
