标签:return 数论 ll sqrt II pmod rho 初等 equiv
1. Miller-Rabin
Miller-Rabin 素性测试是常见的 随机性 素数判定方法。
这里的随机指有一定概率将合数判定为素数,但不会将素数判定为合数。
素数判定的基本思路是,根据所有质数均具有但很少合数具有的性质,检查被判定的数是否具有这些性质。若不具有,则可断定该数是合数,否则该数有很大概率是质数(但并不确定)。
1.1 Fermat 素性检验
我们知道,当 \(p\) 是素数时,对于任意 \(a \perp p\) 均有 \(a ^ {p - 1}\equiv 1 \pmod p\)。反之,当 \(a ^ {p - 1} \equiv 1\pmod p\) 时,是否有 \(p\) 是素数?如果命题成立,那么判断一个数是否是素数只需要一遍快速幂。
可惜命题并不成立。有很小的概率使得 \(a \perp p\),\(p\) 是合数且 \(a ^ {p - 1} \equiv 1\pmod p\),例如当 \(a = 2\),\(p = 341\) 时,\(2 ^ {340} \equiv 1 \pmod {341}\)。这种情况称为 \(341\) 是以 \(2\) 为底的伪素数。\(341\) 是最小的伪素数基数。
但是若 \(a ^ {p - 1}\not \equiv 1\pmod p\),则 \(p\) 必然不是质数。为此,考虑多选几个与 \(p\) 互质的数检查,这样可以排除大部分合数。这被称为 Fermat 素性检验。显然,它带有随机性。
当面对形如 \(561\) 的卡迈克尔数时,Fermat 素性检验就束手无策了,因为卡迈克尔数 \(p\) 满足所有与 \(p\) 互质的数的 \(p - 1\) 次方模 \(p\) 均为 \(1\)。这说明 Fermat 素性检验仍不够优秀。
1.2 二次探测定理
根据高次剩余部分的知识,当 \(p\) 为奇素数时,\(x ^ 2\equiv 1\pmod p\) 仅有解 \(\pm 1\)。因此,对于 \(p\) 而言,若存在 \(a \neq \pm 1\) 满足 \(a ^ 2 \equiv 1\pmod p\),则 \(p\) 必然不是质数。
这被称为二次探测定理。
1.3 算法介绍
考虑将二次探测定理和费马素性检验合起来用。
根据二次探测定理,当 \(a ^ {p - 1} \equiv 1\pmod p\) 时,若 \(p - 1\) 是 \(2\) 的倍数,则 \(a ^ {\frac {p - 1} 2}\) 必须是 \(\pm 1\)。若 \(\dfrac {p - 1} 2\) 仍是 \(2\) 的倍数且 \(a ^ {\frac {p - 1} 2}\equiv 1\pmod p\),则 \(a ^ {\frac {p - 1} 4}\) 必须是 \(\pm 1\),以此类推。
简单地说,若 \(p - 1\) 是 \(2 ^ r\) 的倍数且 \(a ^ {\frac {p - 1}{2 ^ {r - 1}}} \equiv 1\pmod p\),则 \(a ^ {\frac {p - 1}{2 ^ r}}\) 必须等于 \(\pm 1\),否则就不是素数。
例如 \(a = 2\) 且 \(p = 341\)。\(2 ^ {340} \equiv {341}\),\(2 ^ {170} \equiv 1\pmod {341}\),但 \(2 ^ {85} \equiv 32\pmod {341}\)。这说明 \(341\) 不是质数。
这样检测的准确率相当高。事实上,随机选择 \(k\) 个底数,则 Miller-Rabin 算法的正确性(指不会将合数误判成素数的概率)为 \(1 - 4 ^ {-k}\),时间复杂度为 \(\mathcal{O}(k \log ^ 2 n)\)(若将快速幂视为一个 \(\log\) 而非关于值域的三个 \(\log\))。
注意到 Miller-Rabin 的效率和选取底数个数有关,我们自然希望底数越少越好,同时要保证一定的正确性。以下是常用底数(来自 wangrx 的博客,在此感谢他)。
- 对 \(2 ^ {32}\) 以内的数判素,使用 \(2, 7, 61\) 三个底数。
- 对 \(2 ^ {64}\) 以内的数判素,使用 \(2,325,9375,28178,450775,9780504,1795265022\) 七个底数。
- 使用前 \(12\) 个素数作为底数可以对 \(318665857834031151167460(3\times 10 ^ {23} \approx 2 ^ {78})\) 以内的数判素。详见 A014233 - OEIS。
- 注意,在固定底数时,需要对底数特判。即若以 \(2, 7, 61\) 作为底数,则当 \(n = 2, 7\) 或 \(61\) 时需直接特判通过检验,因为 \(p\) 无法通过以 \(p\) 为底的素性检验。
mt19937 rnd(time(0));
#define ll long long
int rd(int l, int r) {return rnd() % (r - l + 1);}
ll ksm(ll a, ll b, ll p) {
ll s = 1;
while(b) {
if(b & 1) s = (__int128) s * a % p;
a = (__int128) a * a % p, b >>= 1;
}
return s;
}
bool Miller_Rabin(ll n) {
if(n < 3 || n % 2 == 0) return n == 2;
for(int i = 1; i <= 10; i++) {
int x = rd(1, 1e9) % (n - 2) + 2;
if(ksm(x, n - 1, n) != 1) return 0;
for(ll j = n - 1; j & 1 ^ 1;) {
ll val = ksm(x, j >>= 1, n);
if(val == n - 1) break;
if(val != 1) return 0;
}
}
return 1;
}
1.4 复杂度优化
Miller-Rabin 的复杂度和正确性足够优秀,但我们注意到在整个过程中我们多次使用快速幂计算 \(a\) 的幂,且指数每次除以 \(2\)。这很浪费。
考虑将整个过程反过来,即预先处理好 \(p - 1 = r \cdot 2 ^ d\),然后计算 \(a ^ r\) 并执行 \(d\) 次平方操作,即可得到每个 \(a ^ {r \cdot 2 ^ i}\)。这样,时间复杂度优化为 \(\mathcal{O}(k\log n)\),尽管在 OI 中应该没有毒瘤出题人会扣这个细节。
更进一步地,首先判掉 \(a ^ r\equiv 1\pmod p\),此时 \(p\) 通过了本轮检验(但并不一定是素数)。否则若 \(p\) 是质数,说明在 \(i\) 从 \(d\) 减小到 \(0\) 的过程中,\(a ^ {r \cdot 2 ^ i}\bmod p\) 必然经历了从 \(1\) 变为 \(-1\) 的过程(如果 \(a ^ {r \cdot 2 ^ d} \not\equiv 1\pmod p\),则 \(p\) 甚至没有通过 Fermat 素性检验)。
因此,我们只需判断是否存在 \(0\leq i < d\) 使得 \(a ^ {r \cdot 2 ^ i} \equiv -1 \pmod p\)。容易证明这是 \(p\) 通过该轮素性检验的充要条件。
bool Miller_Rabin(ll n) {
if(n < 3 || n % 2 == 0) return n == 2;
ll r = n - 1, d = 0;
while(r & 1 ^ 1) r >>= 1, d++;
for(int i = 1; i <= 10; i++) {
ll x = rd(1, 1e9) % (n - 2) + 2, v = ksm(x, r, n);
if(v == 1) continue;
for(int j = 0; j <= d; j++) {
if(j == d) return 0;
if(v == n - 1) break;
v = (__int128) v * v % n;
}
}
return 1;
}
2. Pollard-rho
分解质因数一般使用的试除法的时间复杂度为 \(\mathcal{O}(\sqrt n)\),因为我们必须枚举到 \(\sqrt n\) 才能确定 \(n\) 是一个质数。
Pollard-rho 算法为时间复杂度又开了一次平方,它可以在期望 \(\sqrt[4]{n}\) 的时间复杂度内求出 \(n\) 的一个非平凡因子。因此使用 Pollard-rho 分解质因数的时间复杂度为 \(\sqrt [4]{n}\omega(n)\)。
2.1 生日悖论
相信读者都或多或少了解过这一悖论,这里简单讲一下。
从 \(1\sim n\) 的正整数中 \(k\) 次等概率随机选出一个数(可重复),则所有数互不相同的概率为
\[P = \dfrac {n ^ {\underline{k}}} {n ^ k} \]这个公式的含义是从 \(n\) 个数中有序地 \(k\) 个数的方案数除以总方案数。
- 直观认知:当 \(k\) 增大时,\(P\) 衰减得相当快,因为每次 \(\dfrac {n - k + 1} n\) 均以相乘的方式作用在 \(P\) 上。可以理解为指数衰减,但没有指数衰减那么快,因为分子也相当大。如下图。
经过手玩函数图像后,我们发现使得 \(P = \dfrac 1 2\) 的 \(k\) 似乎是 \(\sqrt n\) 级别的。
证明详见 OI Wiki,我们只需要记住结论:每次在 \(n\) 个数中等概率随机选择一个,使得所有选出的数中存在两个相同的期望次数为 \(\mathcal{O}(\sqrt n)\)。
2.2 算法介绍
Pollard-rho 算法的巧妙之处在于构造伪随机函数 \(f(x) = x ^ 2 + c\)。
因为 \(f\) 仅含有一个变量,因此对于相同的 \(x\),\(f(x)\) 给出的值也均相同。选取 \(f\) 的好处是在进入循环前,不断迭代得到的数可近似看做随机。其随机性不作证明(也许和曼德勃罗集的混沌属性有关)。
根据生日悖论,在模 \(n\) 意义下,若给定 \(c\) 和初始值 \(x_0\)(一般以 \(0\) 作为初始值),则 \(f\) 在不断迭代的过程中(即 \(x_0, x_1= f(x_0), x_2 = f(x_1), \cdots, f_i = f ^ i(x)\),\(x_i\) 均对 \(n\) 取模)期望 \(\sqrt n\) 次进入一个长为 \(\sqrt n\) 的循环。
因为整条路径酷似希腊字母 \(\rho\),算法得名 Pollard-rho。记 \(x_i\) 在模 \(n\) 意义下形成的路径为 \(\rho_n\),如下图。
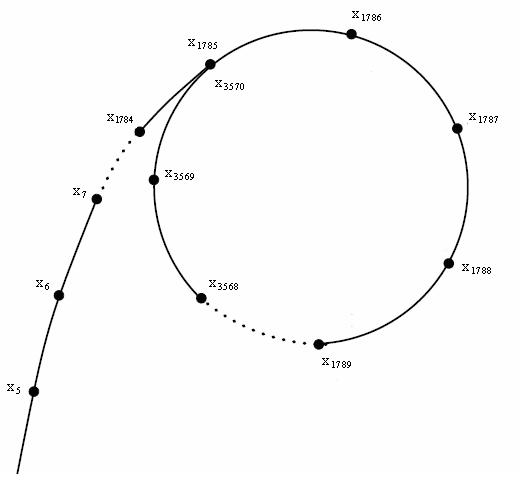
若 \(n\) 为合数,则其最小非平凡因子 \(m\) 的级别不超过 \(\sqrt n\)。这说明在模 \(m\) 意义下 \(x_i\) 期望 \(\sqrt [4]{n}\) 次进入一个长为 \(\sqrt [4]{n}\) 的循环。记 \(x_i\) 在模 \(n\) 意义下形成的路径为 \(\rho_m\)。
同时,若模 \(m\) 一旦进入循环(即存在 \(x_i \equiv x_j\pmod m\)),我们就可以通过将 \(|x_i - x_j|\) 和 \(n\) 取 \(\gcd\) 来求出 \(m\)(或者它的倍数),前提是 \(x_i \not\equiv x_j\pmod n\)。
现在的问题是求出一组 \(i, j\) 使得 \(i, j\) 处于 \(\rho_m\) 上的同一点,但处于 \(\rho_n\) 上的不同点。也就是,\(i\) 需要足够大(据分析,级别为 \(\sqrt [4]{m}\)),使得跳出 \(\rho_m\) 的尾巴,且 \(j - i\) 恰好是 \(\rho_m\) 的循环节的倍数。
注意在整个过程中我们不知道 \(m\),但通过分析可以证明求得 \(m\) 的的期望复杂度为 \(\sqrt [4]{n}\)(我们将说明如何去掉 \(\gcd\) 的 \(\log\) 因子)。求得的非平凡因子也不一定最小,因此还需继续分解。
介绍两个解决上述问题的常见方法。
考虑直接令 \(j = 2i\),然后从小到大枚举 \(i\),不断计算 \(\gcd(|x_{2i} - x_i|, n)\) 直到该值不等于 \(1\)。
此时有两种情况,一是小于 \(n\),这说明该值即 \(n\) 的一个非平凡因子,直接返回。二是等于 \(n\),这说明我们进入了 \(\rho_n\) 的循环节,有很大概率 \(\rho_n\) 的环长等于 \(\rho_m\) 的环长,也有可能是 \(\rho_m\) 的尾巴过长,使得第一次在枚举到 \(\rho_m\) 的环长的倍数使得 \(i\) 跳出 \(\rho_m\) 的尾巴时就枚举到了 \(\rho_n\) 的环长。无论如何,这意味着我们应该结束本次失败的 Pollard-rho,调整参数 \(c\) 重新分解。 期望时间复杂度 \(\sqrt [4]{n} \log n\)。
上述算法被称为基于 Floyd 判环的 Pollard-rho 算法。
- Note:笔者在实现了 Floyd 判环后,发现若初始令 \(i = 1\),\(j = 2\),则对于 \(n = 4\) 无论如何也分解不出来。需要初始令 \(i = 0\),\(j = 1\)(或特判 \(n = 4\)),然后每次 \(i \gets i + 1\),\(j \gets j + 2\)。
优化:注意到 \(\gcd\) 调用次数过多会显著降低效率,朴素的 Floyd 判环法无法通过模板题。我们考虑设置 “样本累计上限” \(T\),将 \(T\) 组 \(\gcd\) 测试打包在一起,其正确性基于 \(\gcd(a, n) \mid \gcd(ab\bmod n, n)\)。\(T\) 取 \(10\) 时在模板题数据下表现较为优秀。这样可以将复杂度中的 \(\log\) 因子去掉。
ll n, c, s, t;
ll f(ll x) {return ((__int128) x * x + c) % n;}
ll Pollard_rho(ll _n) {
n = _n, c = rd(0, 1e9) % ((n = _n) - 1) + 1, s = f(t = 0); // 注意 t = 0 而不能 t = c
ll acc = 0, prod = 1, d;
while(s != t) {
prod = (__int128) prod * abs(s - t) % n;
if(++acc == 10) {
if((d = __gcd(prod, n)) > 1) return d;
acc = 0;
}
s = f(f(s)), t = f(t);
}
if((d = __gcd(prod, n)) > 1) return d;
return n;
}
二分一个未知上界的数的最好方法是倍增。于是我们固定 \(i = 2 ^ k\),\(j\) 取遍 \([2 ^ k + 1, 2 ^ {k + 1}]\),检查即可。同样的,需要考虑到 \(i = 0\),\(j = 1\) 的情况,或特判 \(n = 4\)。
倍增法也需要样本累计优化加持,即每 \(T\) 组 \(|x_i - x_j|\) 样本打包在一起,相乘后求 \(\gcd\)。对于倍增法而言,通常使用 \(T = 127\)。代码见例题 I.
- Note:如果担心 \(n\) 较小时算法的正确性,可以暴力分解质因数。读者需要认识到 Pr 本身是一个随机算法的本质。对于一些广为流传的 Pr 写法,前人已经验证过了其在一定范围内的正确性,所以我们只需放心大胆地使用即可。
总之,求解 \(i, j\) 的方法多种多样,但样本累计优化去掉 \(\log\) 因子是核心。检查太耗时则将若干次检查打包在一起,这样的思想方法不仅可用于优化 Pollard-rho,也可以应用在 OI 的其他各个领域。
2.3 例题
I. P4718【模板】Pollard-Rho 算法
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(0));
#define ll long long
int rd(int l, int r) {return rnd() % (r - l + 1);}
ll ksm(ll a, ll b, ll p) {
ll s = 1;
while(b) {
if(b & 1) s = (__int128) s * a % p;
a = (__int128) a * a % p, b >>= 1;
}
return s;
}
bool Miller_Rabin(ll n) {
if(n < 3 || n % 2 == 0) return n == 2;
ll r = n - 1, d = 0;
while(r & 1 ^ 1) r >>= 1, d++;
for(int i = 1; i <= 10; i++) {
ll x = rd(2, n - 1), v = ksm(x, r, n);
if(v == 1) continue;
for(int j = 0; j <= d; j++) {
if(j == d) return 0;
if(v == n - 1) break;
v = (__int128) v * v % n;
}
}
return 1;
}
ll Pollard_rho(ll n) {
ll c = rd(1, n - 1), s = 0, t = 0, prod = 1;
for(int i = 1; ; s = t, i <<= 1)
for(int j = 1; j <= i; j++) {
t = ((__int128) t * t + c) % n, prod = (__int128) prod * abs(s - t) % n;
if((j % 127 == 0 || j == i) && __gcd(prod, n) > 1) return __gcd(prod, n);
}
}
ll maxprime(ll n) {
if(n == 1) return 1;
if(Miller_Rabin(n)) return n;
ll p = Pollard_rho(n);
while(p == n) p = Pollard_rho(n);
while(n % p == 0) n /= p;
return max(maxprime(p), maxprime(n));
}
int main() {
ll T, n;
cin >> T;
while(T--) {
cin >> n;
if(Miller_Rabin(n)) {puts("Prime"); continue;}
cout << maxprime(n) << endl;
}
return 0;
}
3. 参考资料
第一章:
第二章:
标签:return,数论,ll,sqrt,II,pmod,rho,初等,equiv 来源: https://www.cnblogs.com/alex-wei/p/Number_Theory_II.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。