标签:le frac 周期 Border 杂谈 Period border displaystyle gcd
十分简要地胡乱说一些与 Border 相关的东西。
Border 是什么?
用 kmp 求的那个东西就是 border,因此 border 可以在 \(\mathcal O(n)\) 内用 kmp 求出来,每个前缀的 border 构成树形结构,把这个树建出来,我们称其为失配树。
Border 的性质
弱周期引理(Weak Periodicity Lemma,WPL)
若 \(p,q\) 为 \(S\) 的周期,且 \(p+q\le |S|\),那么 \(\gcd(p,q)\) 也是 \(S\) 的周期。
证明:不妨设 \(p<q\),令 \(d=q-p\),那么:
- 当 \(i<q\) 时,\(S[i]=S[i+q]=S[i+q-p]=S[i+d]\);
- 当 \(i>p\) 时,\(S[i]=S[i-p]=S[i-p+q]=S[i+d]\);
不难发现 \(i\) 取遍 \([1,|S|]\),因此 \(d\) 也为 \(S\) 的周期,根据辗转相除法,可证 \(\gcd(p,d)\) 为 \(S\) 的周期。
周期定理(Periodicity Lemma,PL)
若 \(p,q\) 为 \(S\) 的周期,且 \(p+q-\gcd(p,q)\le |S|\),那么 \(\gcd(p,q)\) 也是 \(S\) 的周期。
它比 WPL 稍微强一点在于对 \(p,q\) 的限制。用得少,不证它了。
前缀整除周期传递性
若 \(S\) 是 \(T\) 的前缀,且 \(T\) 有周期 \(a\),\(S\) 有周期 \(b\),\(b\mid a\land |S|\ge a\),则 \(T\) 也有周期 \(b\).
证明:画个图就行。
长串等差匹配位
若 \(2|S|\ge |T|\),则 \(S\) 在 \(T\) 中的匹配位置必为等差序列.
证明:先将 \(T\) 中没有被 \(S\) 覆盖的部分去掉,由于 \(2|S|\ge |T|\),因此此时的 \(T\) 的所有部分都被 \(S\) 覆盖。
对于 \(S\) 在 \(T\) 中的匹配位小于等于 \(2\),结论是显然的,下面考虑匹配位大于 \(2\) 的情况。
设 \(S\) 在 \(T\) 中第一二次的匹配位差为 \(d\),第二次与后面的某一次匹配位差为 \(q\),不难发现 \(d,q\) 均为 \(S\) 的周期,并且显然有 \(d+q+|S|\le |T|\),并且 \(2|S|\ge |T|\),可得 \(d+q\le |S|\),由 WPL 得 \(r=\gcd(d,q)\) 为 \(S\) 的周期。设 \(p\) 为 \(S\) 的最小周期,那么有 \(p\mid r\),否则 可以使用 WPL 构造更小的周期。此时 \(p\mid r\mid d\).
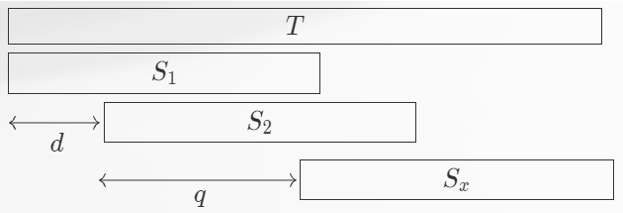
若 \(p<d\),那么,由于 \(p\) 是 \(S\) 的循环,因此我们可以找到一个距离第一匹配位距离比 \(d\) 更小的第二匹配位,与 \(d\) 的定义矛盾。
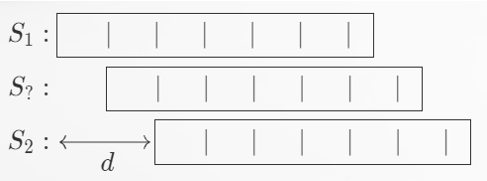
因此只有可能是 \(p=r=d\),又因为 \(r=\gcd(d,q)=d\),因此 \(d\mid q\),所以匹配位在处理之后的 \(T\) 上,从位置 \(1\) 开始,每 \(d\) 个出现一次。还原到原来的 \(T\) 串上,匹配位就是公差为 \(d\) 的等差数列了。
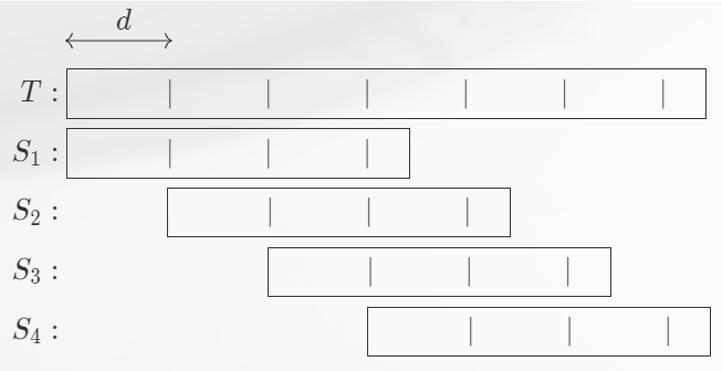
长 border 等差匹配位
\(S\) 的长度达到 \(\displaystyle \frac{n}{2}\) 的 border 的长度构成等差序列。
设 \(n-p,n-q\) 为 \(S\) 的两个长度达到 \(\displaystyle \frac{n}{2}\) 的 border,且 \(n-p\) 是最大的 border,那么 \(p\) 为 \(S\) 的最小周期,且 \(p,q\) 均为 \(S\) 的周期,由于 \(\displaystyle n-p>n-q\ge \frac{n}{2}\),因此 \(p+q\le n\),因此 \(r=\gcd(p,q)\) 也为 \(S\) 的周期,由于 \(p\) 是 \(S\) 的最小周期,因此 \(r=p\),即 \(p\mid q\),且 \(p\) 是最小周期,因此所有的 border 长度以 \(p\) 为公差构成等差序列。
不难发现,实际上 \(n-kp\) 都是 \(S\) 的 border,因为既然 \(p\) 为周期,那么 \(2p,3p,\cdots\) 均为周期,进而说明 \(n-2p,n-3p,\cdots\) 均为 border.
长 border 大一统
设 \(n-p\) 为 \(S\) 的最大 border,如果 \(\displaystyle n-p\ge \frac{n}{2}\),那么所有 \(S\) 的长度在 \([p,n-p]\) 的 border 都是 \(n-kp\) 的形式,并且不存在其他形式。
采用反证法,设 \(n-r\) 也是长度在 \([p,n-p]\) 的 border,且不是 \(n-kp\) 的形式。由于 \(p\) 也是周期,因此我们显然可以将这个 \(r\) 进行 \(\pm p\) 来任意调整。
假设 \(r\in [kp,(k+1)p)\),显然我们可以找到一个 \(q\in [kp,(k+1)p)\) 且 \(p\mid q\),此时,如果 \(r+q\le n\),那么我们就可以使用 WPL 证明 \(d=\gcd(r,q)\le |r-q|<p\) 为周期进而推出矛盾了。
如何达到 \(r+q\le n\) 呢?注意前面,我们可以将 \(r\) 进行调整,显然可以将 \(r\) 对 \(\displaystyle p\le \frac{n}{2}\) 取模,此时保证了 \(\displaystyle r<\frac{n}{2}\),此时 \(r+q\le n\) 了。
当然也可以用前面的等差匹配位来证明,显然可以找到一个 \(t\) 使得 \(\displaystyle n-r+tp\ge \frac{n}{2}\),且 \(n-r+tp\) 也为 border,由等差匹配位,\(n-r+tp\) 应与其他 \(n-kq\) 构成等差序列,此时公差会变小,与 \(p\) 的假设构成矛盾。
等差数列对数级
一个串 \(S\) 的所有 border 按长度排序后,可以被划分成 \(\mathcal O(\log n)\) 个等差序列。
把达到 \(\displaystyle \frac{n}{2}\) 的 border 取出来,就是一个等差序列。然后只需要考虑长度为 \(\displaystyle \frac{n}{2}\) 的前缀 \(S'\),对于 \(S'\),将达到 \(\displaystyle \frac{n}{4}\) 的 border 取出来,又是一个等差序列......因此,只会有 \(\mathcal O(\log n)\) 个等差序列。
标签:le,frac,周期,Border,杂谈,Period,border,displaystyle,gcd 来源: https://www.cnblogs.com/Arextre/p/16069477.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
