标签:二分 复习 wqs WQS 凸包 斜率 DP mathrm
〇、前言 ¶
天天被打爆......很久之前学过 \(\mathrm{wqs}\) 二分,现在又忘记了......考试凭感觉打......还是总结一篇好了。
壹、知识桥 ¶
引入:有若干个物品,要求你选出 \(m\) 个,选的时候带有限制,要你求出最优的方案。
一般解决这一类问题,我们十分常用的技巧是 \(\mathrm{DP}\),不过,在某些限制条件或者数据范围较为严格的时候,\(\mathrm{DP}\) 因为其本身并不具备比较特殊的性质而难以优化,这个时候,\(\mathrm{wqs}\) 二分就应运而生了。
\(\mathrm{wqs}\) 二分有一个十分重要的前提:设 \(g(i)\) 为选择 \(i\) 个物品的最优方案,若将 \((i,g(i))\) 画出来,那么这些点在平面上必须构成凸包,其本质是需要满足斜率的单调性。此时,我们的目的就是求出 \(g(m)\),而 \(\mathrm{wqs}\) 二分的主要算法流程是:
- 二分一个斜率 \(k\);
- 求出直线 \(y=kx+C\)(其中 \(C\) 为一常数)与 \((i,g(i))\) 凸包的切点;
- 根据切点与 \((m,g(m))\) 的关系,对斜率进行调整;
- 反复执行上述三步;
该过程,用一图以蔽之,即:
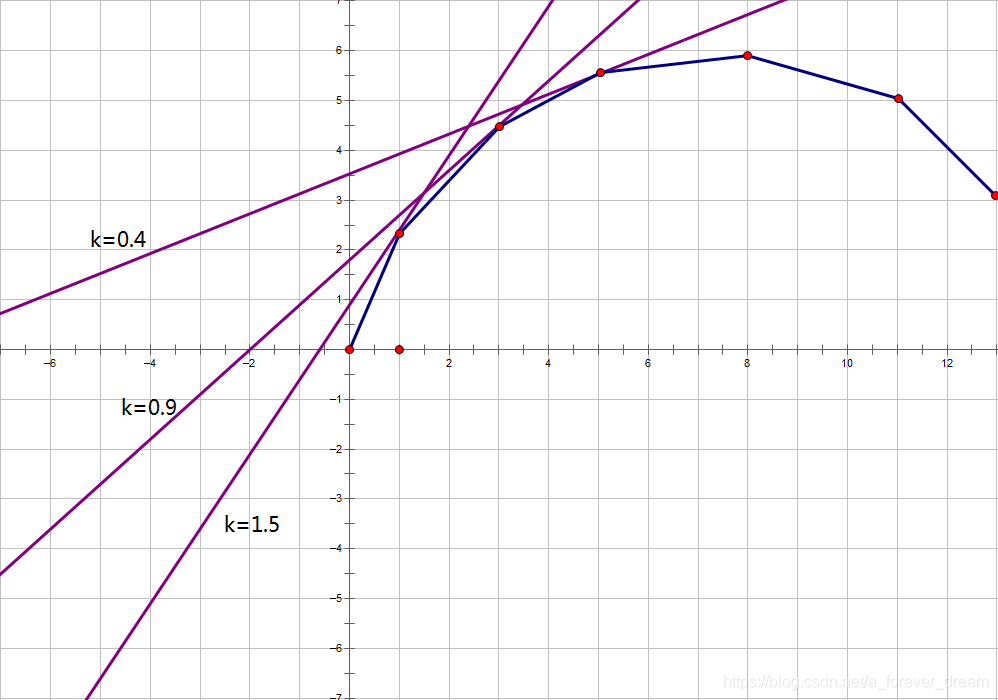
现在似乎无法进一步分析了,但我们可以考察 \(f(x)\) 的含义 —— 选 \(x\) 个物品,每个物品价值减去 \(k\) 之后的最大价值和。由于 \(x\) 为任意数值,因此我们在选的物品数量上并没有任何限制,这在 \(\mathrm{DP}\) 层面,本质就是去掉了限制物品数量的一个维度,替换为了一个 \(\log\) 的二分斜率的时间。
这看上去确实很厉害,不过,仍然要重申一遍使用该方法的前提条件:\((i,g(i))\) 具有凸性,而凸性的证明我们可以从几个方面入手:
- 斜率具有单调性;
- \(\forall i,f(i)>\frac{f(i-1)+f(i+1)}{2}\);
- 从 \(\mathrm{DP}\) 的一些基本性质或含义上入手;
- ......;
还可能有更多的方法,具体情况具体分析咯。另外,还有两个比较细节的地方,一是关于斜率的调整,应当结合图像的上凸或者下凸调整左右边界,二是应当考察一条直线的情形。
贰、典例营 ¶
[APIO/CTSC2007]数据备份
设计朴素状态 \(f(i,j,0/1)\) 表示前 \(i\) 个建筑,选了 \(j\) 对,最后一个建筑是否被选择,于是可以得到比较简单的转移。
不难发现,如果我们固定 \(i=n\),并 \(g(j)\overset\Delta=\min(f(n,j,0),f(n,j,1))\),那么 \((j,g(j))\) 显然是下凸的,具体可以考察其增量,每次肯定都是贪心选择较小的,到了后面单次增量将会逐渐增大,于是我们就可以对其使用 \(\mathrm{wqs}\) 二分。
\(\mathcal{Submission\;Link}\).
[CF958E2]Guard Duty(medium)
注意到 \(2k\le n\),那么,我们每次选择 \(t\) 相邻的肯定最好,设 \(t'\) 为 \(t\) 排序后的结果,记 \(a_i=t'_{i + 1} - t'_i\),那么,原题目就转化为了,从 \(a\) 中选择 \(k\) 个,这 \(k\) 个中没有两个相邻(这意味着相交在端点)的最小值,这和上一个题很相似了,同理可做。
\(\mathcal{Submission\;Link}\).
[CF739E]Gosha is hunting
朴素 \(\mathrm{DP}\) 显然是 \(f(n,i,j)\) 表示考虑到第 \(n\) 只,用了 \(i\) 个 \(a\) 球,\(j\) 个 \(b\) 球之后抓住宝贝的期望值,于是分为三种转移:
- 啥都没使用,\(f(n,i,j)\gets f(n-1,i,j)\);
- 用了 \(a\) 球,\(f(n,i,j)\gets f(n-1,i-1,j)+p_i\);
- 用了 \(b\) 球,\(f(n,i,j)\gets f(n-1,i,j-1)+u_i\);
- 两种都用了,\(f(n,i,j)\gets f(n-1,i-1,j-1)+1-(1-p_i)(1-u_i)\);
不难发现,固定 \(n,i\),将 \((j,f(n,i,j))\) 画到坐标系上,它一定是斜率单调不升的,原因很简单,优先选择概率更大的,再选择概率较小的,于是,我们可以分离出 \(j\) 这一维度,使用 \(\mathrm{wqs}\) 二分来解决。
同样地,我们也可以类似地分离出 \(i\) 这一维度,于是这个题就是两重 \(\mathrm{wqs}\) 套起来,显然斜率的变化范围在 \([0,1]\),我们只需要在这个区间中进行二分即可,当然,若你初始边界设在 \((-\infty,+\infty)\),实际上也没啥问题,不过多了一些没有必要的过程而已。
标签:二分,复习,wqs,WQS,凸包,斜率,DP,mathrm 来源: https://www.cnblogs.com/Arextre/p/15426915.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
