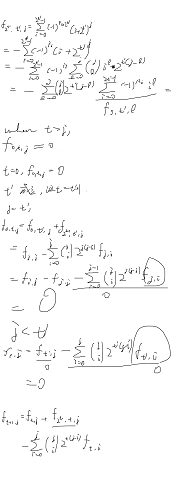标签：NOI limits int 题解 sum rg 2021 res 式子

0.Preface

考试的时候一如既往地被爆踩了/ll
西西弗出题越来越不正经了
Notice:这篇题解同时包含了提高组前两题和入门组的（简化版）题目与解法，对于提高组试题提供了代码。

1.Senior

T1

对于无限 Thue-Morse 数列 \(\{t_i\}\) 的前 \(n\) 项和给定多项式 \(f\)，求 \(\sum\limits_{i=0}^{n-1}t_if(i)\)。
首先来对这个式子进行乱搞，设 \(p_n\) 为 \(n\) 的二进制表示中 \(1\) 的个数，则找规律易知 \(t_i=p_i\bmod2\) 即 \(\dfrac12 [1-(-1)^{p_i}]\)。
那么此时答案就拆成了两个稍简单的式子：\(\dfrac12[\sum\limits_{i=0}^{n-1}f(i)-\sum\limits_{i=0}^{n-1}(-1)^{p_i}f(i)]\)。
前一个式子是 \(k-1\) 次多项式的前缀和，可以参照此题插值求出，重点在后一个式子。
与前一个式子一样，求和的重点是 \(\sum\limits_{i=0}^{n-1}(-1)^{p_i}i^k\)。
由于题目暗示得很明显，我们可以尝试将 \([0,n)\) 拆分成几个区间，而区间之间要有一些关系可以方便地进行平移等操作。
对于一个数 \(n\)，我们把它从高位到低位划分就可以得到一些特殊性质，以下给出了一个例子。
设 \(n=(1010110)_2\)，我们将其分为四个区间：
\([0000000,1000000)\cup[10000000,1010000)\cup[1010000,1010100)\cup[1010100,1010110)\)。
接下来我们的任务就是对于每个偏移量 \(d\) 和某一位 \(t\)，计算 \(f_{d,t,k}=\sum\limits_{i=0}^{2^t-1}(-1)^{p_{(i+d)}}\ (i+d)^k\)。
这时候划分方式的作用就体现出来了：从 \(d\) 到 \(d+2^t-1\) 这些数变化的数位对 \(d\) 没有影响，所以这个式子可变形为 \((-1)^{p_d}\sum\limits_{i=0}^{2^t-1}(-1)^{p_i}(i+d)^k\)。
把后面的幂暴力展开再蹂躏一番得到以下式子：\(f_{d,t,k}=(-1)^{p_d}\sum\limits_{j=0}^k\dbinom{k}{j}d^{k-j}f_{0,t,j}\)。
所有 \(f_{0,t,j}=f_{0,t-1,j}+f_{2^{t-1}\ ,t-1,j}\) 可以倍增预处理出来，最终总复杂度为 \(O(k^2(\log n+k))\)。
但是，这样是不够好的！我们需要优化！
有些题解里直接根据打表得出结论是不妥当的，这里参考官方题解给出一个简易证明：
首先推得 \(f_{2^t,t,j}=-\sum\limits_{i=0}^j\dbinom{j}{i}2^{t(j-i)}f_{0,t,i}\)（显然）。
所以 \(f_{0,t+1,j}\) 就等于 \(f_{0,t,j}\) 加上上面的东西。
证明：\(t>j\) 时 \(f_{0,t,j}=0\)。
运用数学归纳法：固定一个 \(j\)，显然 \(t=0\) 时成立。考虑 \(t'\) 成立时证明 \(t=t'+1\) 也成立。
1.若 \(j=t'\)，则 \(f_{0,t,j}=f_{0,j,j}-\sum\limits_{i=0}^{j}\dbinom{j}{i}2^{j(j-i)}f_{0,j,i}=f_{0,j,j}-f_{0,j,j}-\sum\limits_{i=0}^{j-1}\dbinom{j}{i}2^{j(j-i)}f_{0,j,i}=0-0-0=0\)；
2.若 \(j<t'\)，则 \(f_{0,t,j}=f_{0,t',j}-\sum\limits_{i=0}^j\dbinom{j}{i}2^{t'(j-i)}f_{0,t',i}=0-0=0\)。
所以 \(t>j\) 时 \(f_{0,t,j}=0\)。\(\blacksquare\)
如果还不明白的话请看更详细的草稿吧（虽然根本看不清楚）

可以明显看出作者快证出来时笔法逐渐猖狂
由于作者水平所限，如证明过程出现纰漏敬请指出。
关于代码实现，先插值求出减号前部分，再利用公式计算减号后的部分，有非常多的细节，请仔细编写（我是照着洛谷题解改的）。
一些预处理的总复杂度为 \(O(\log n)\)，减号前复杂度为 \(O(k^2)\)，减号后复杂度为 \(O(k^3)\)，最终总复杂度为 \(O(\log n+k^3)\)。

const int N=500010,K=510,p=1000000007;
int n,nn,k,a[K],ans1,ans2;char s[N];
int C[K][K],pw2[N];
il void Init(){
  for(rg int i=0;i<=k;i++){
    C[i][0]=C[i][i]=1;
    for(rg int j=1;j<i;j++){
      C[i][j]=(C[i-1][j]+C[i-1][j-1])%p;
    }
  }
  pw2[0]=1;
  for(rg int i=1;i<=n;i++)pw2[i]=2ll*pw2[i-1]%p;
  for(rg int i=0;i<n;i++)nn=(2ll*nn+s[i]-48)%p;
  nn=(nn-1+p)%p;
}
il int Pow(int a,int b){
  int res=1;
  while(b){
    if(b&1)res=res*a%p;
    a=a*a%p,b>>=1;
  }
  return res;
}
int f[K][K];
//f_{t,j}=f_{t-1,j}-\sum_i\binomji 2^{t(j-i)}f_{t,i}
il int Calc(int t,int j){
  if(t>j)return 0;
  if(f[t][j]!=-1)return f[t][j];
  if(!t)return j==0;
  int res=Calc(t-1,j),pw=pw2[t-1],w=1;
  for(rg int i=j;i>=0;i--,w=w*pw%p){
    res=(res-C[j][i]*w%p*Calc(t-1,i)%p+p)%p;
  }
  return f[t][j]=res;
}
int fac[K],inv[K],pre[K],suf[K];
il int CalcFunc(int x){//Calculate f
  int res=0;
  for(rg int i=k-1;i>=0;i--){
    res=(1ll*res*x%p+a[i])%p;
  }
  return res;
}
int sumf[K],ff[K];
il void InitLagrange(){
  fac[0]=pre[0]=suf[k+2]=1;
  for(rg int i=1;i<=k+1;i++)fac[i]=fac[i-1]*i%p;
  inv[k+1]=Pow(fac[k+1],p-2);
  for(rg int i=k;i>=0;i--)inv[i]=inv[i+1]*(i+1)%p;
  sumf[0]=CalcFunc(0);
  for(rg int i=1;i<=k+1;i++){
    sumf[i]=(sumf[i-1]+CalcFunc(i))%p;
    ff[i]=sumf[i]*inv[i-1]%p*inv[k+1-i]%p;
    if((i^k+1)&1)ff[i]=p-ff[i];
  }
}
il int Lagrange(int m){
  int res=0;
  for(rg int i=1;i<=k+1;i++)pre[i]=pre[i-1]*(m-i)%p;
  for(rg int i=k+1;i;i--)suf[i]=suf[i+1]*(m-i)%p;
  for(rg int i=1;i<=k+1;i++){
    res=(res+ff[i]*pre[i-1]%p*suf[i+1]%p)%p;
  }
  return res;
}
void Solve(){
  int lst=0,lpp=0;
  for(rg int i=0;i<n;i++){
    int t=n-i-1;
    int now=(2ll*lst+s[i]-48)%p,pp=lpp^(s[i]-48);
    if(t>k){
      lst=now,lpp=pp;continue;
    }
    if(s[i]==49){
      int pw=lst*pw2[t+1]%p;
      for(rg int j=0;j<k;j++){
        int sum=0,w=1;
        for(rg int l=j;l>=0;l--,w=w*pw%p){
          sum=(sum+C[j][l]*w%p*Calc(t,l)%p)%p;
        }
        if(lpp)sum=p-sum;
        ans2=(ans2+a[j]*sum%p)%p;
      }
    }
    lst=now,lpp=pp;
  }
}
signed main(){
  memset(f,-1,sizeof(f));
  scanf("%s",s),n=strlen(s);
  Read(k);
  for(rg int i=0;i<k;i++)Read(a[i]);
  Init(),InitLagrange(),ans1=Lagrange(nn);
  Solve();
  int ans=(ans1-ans2+p)%p*((p+1)/2)%p;
  cout<<ans<<endl;
  KafuuChino HotoKokoa
}

所以 €€£ 是玩自然数幂和玩上瘾了吗

T2

给定两字符串\(s,t\)，求\(s\)中有多少种子序列能够对应\(t\)中一子段。
枚举 \(t\) 的子串然后从 \(s\) 中顺次匹配即可（具体见代码），至于去重可以存一下哈希值。

const int N=3010,bas=13331,mod=1991122519911223;//关于模数和进制：能过就行
int n;char s[N],t[N];
int q[N*N];
signed main(){
  scanf("%lld%s%s",&n,s+1,t+1);
  for(rg int i=1;i<=n;i++){
    int val=0,p=1;
    for(rg int j=i;j<=n;j++){
      while(p<=n&&s[p]!=t[j])p++;
      if(p>n)break;
      val=(1ll*val*bas%mod+t[j]-96)%mod;
      q[++q[0]]=val;
      p++;
    }
  }
  sort(q+1,q+1+q[0]);
  cout<<unique(q+1,q+1+q[0])-q-1<<endl;
  KafuuChino HotoKokoa
}

T3

\(n\)个点分别有两个权值\(a_i,b_i\)，给定多组\(l,r,c,d\)，求\(\#\{x\in[l,r]|a_x\ \text{xor}\ c\le\min\{b_x,d\}\}\)
不会，爬了。

2.Junior

T1

一个圆只能沿直径切，最少切多少刀能切出\(a:b:c\)
容易证明，最多只需要切三次，于是对不同情况分类讨论。

T2

在一个\(n\)阶方阵上找两条路径使得两条路径的并权值和最大
路径指按照\(45^\circ\)直走（遇墙反弹）出的回路
发现路径只有 \(O(n)\) 条，那么把所有路径预处理出来，枚举两条路径再特判重复的点即可（可能需要亿些分类讨论）。

T3

一个\(n\)阶方阵上有一些障碍和两个球，求按照 2048 的规则将两球合并的最小滑动次数
由移动规则可知，只有障碍物（包括边界）周围的四个点是可以到达的，所以把这些状态记下来，再在可达的状态之间连边。
状态比较多，我们考虑从最终重合的状态逆推，用 BFS 求出最短路即可。

标签：NOI,limits,int,题解,sum,rg,2021,res,式子
来源： https://www.cnblogs.com/juruoajh/p/14588881.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。