标签:Slope 直线 le 入门 多项式 斜率 ge dp
\(\Large \text {斜率优化}\)
前置芝士:单调队列优化的\(DP\),平面直角坐标系,一次函数,可能需要的线性规划思想。
我们设\(dp_i\)为处理到\(i\)时的最小费用,\(S_i=\sum_{k=1}^i c_k\)则有:
\[dp_i=\min_{0\le j<i}\{dp_j+(S_i-S_j)^2+M\} \]将其展开,得到:
\[dp_i=\min_{0\le j<i}\{dp_j+S_i^2+S_j^2-2*S_i*S_j+M\} \]\(\min\)很烦,将其去掉,顺便将只有\(j\)的项移到一边,剩下的放一起。
\[dp_j+S_j^2=2*S_i*S_j+(dp_i-S_i^2-M) \]仔细观察这条柿子,将与\(j\)有关的看作变量,其他的视为变量(因为在我当前这个状态,\(i\)是已知的),像不像一次函数\(y=kx+b?\)
现在我们构建一个以\(2*S_j\)为横坐标,\(dp_j+S_j^2\)为纵坐标的平面直角坐标系: (下文以\(X_j\),\(Y_j\)代替)
而每一个点\((X_j, Y_j)\),都在这上面。
每个决策\(i\)所对应有个斜率\(S_i\)
可以知道,我们如果选取点\(k\)的话,只要将我们当前的直线\(f(x)=S_i*x+b\)向上平移,即可得到一个截距\(b=dp_i-S_i^2-M\),所以当\(b\)去到最小值时,\(dp_i\)就取到最小值。
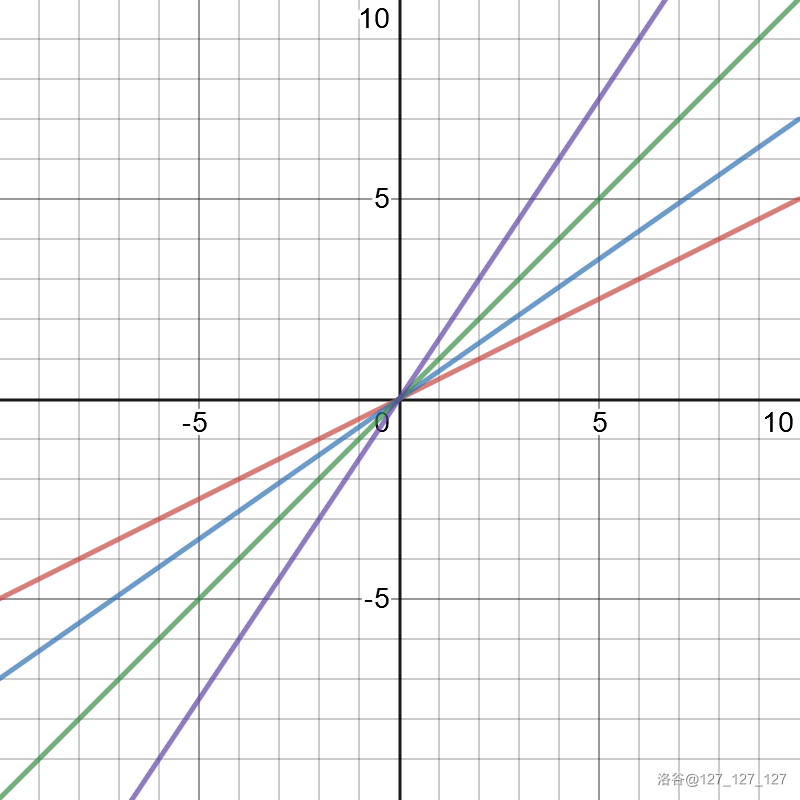
每条直线所对应的斜率:\(Purple:1.5\ Green:2\ Blue:0.75\ Red:0.5\)
考虑维护一个单调队列,这个队列要满足什么呢?
由于一堆点的操作比较难弄,我们考虑三个以内的点的操作。
从对头入手:
令队头为\(q_h\),队里第二个元素为\(q_{h+1}\),则使得队头\(q_h\)不优的条件为:
\[dp_{q_h}+S_i^2+S_{q_h}^2-2*S_i*S_{q_h}+M \ge dp_{q_{h+1}}+S_i^2+S_{q_{h+1}}^2-2*S_i*S_{q_{h+1}}+M \]删去无用的:
\[dp_{q_h}+S_{q_h}^2-2*S_i*S_{q_h} \ge dp_{q_{h+1}}+S_{q_{h+1}}^2-2*S_i*S_{q_{h+1}} \]①
移项,换元,得:
\[\frac {Y_{q_{h+1}}-Y_{q_h}} {(X_{q_{h+1}}-X_{q_h})} \le S_i \]接下来以数、形两种角度介绍为什么可以这么干。
数学上很好解释,看回①,\(q_h\)对\(i\)的贡献不如\(q_{h+1}\),那么它以后都没用了,排掉。
再从形上讲:
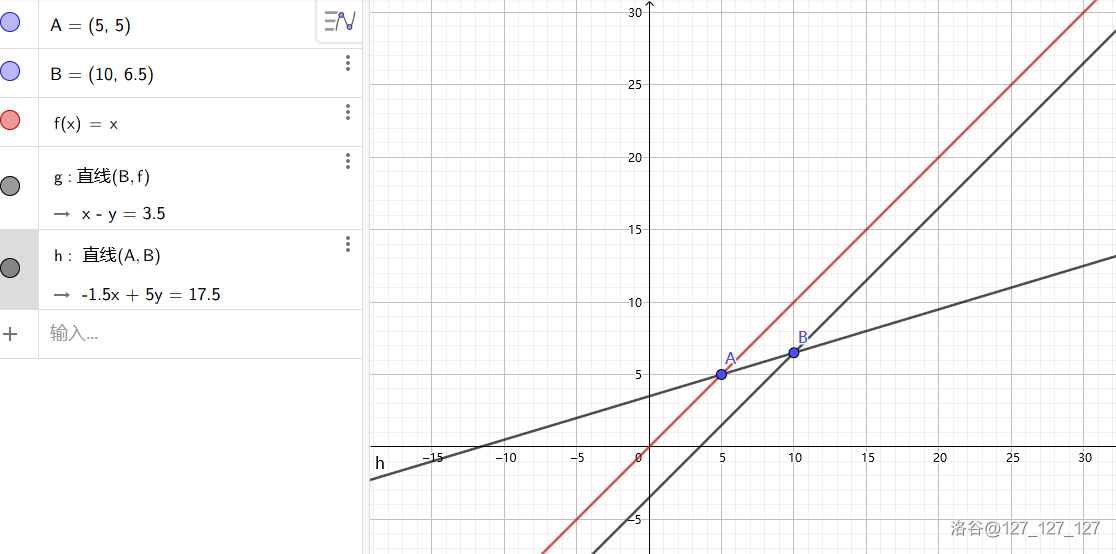
\(RT\),\(A\)为\(q_h\),\(B\)为\(q_{h+1}\)可以看到,如果直线\(l_i\)平移到\(A,B\),会与\(y\)轴产生两个交点,如果直线\(AB\)的斜率\(k_{AB}\le 2*S_i\),即图中的情况,那么\(q_h\)是没用的。
你的脑瓜子就会想出一个问题:
那它会对后来的\(i\)产生贡献啊!
再次回看这条直线的斜率:\(S_i=\sum_{k=1}^i c_k\),因为问题中的\(c_i \ge 0\) 所以\(S_i\)非严格单调递增。
即:
这条直线只会越来越斜。
那我们把线变斜一点试试:
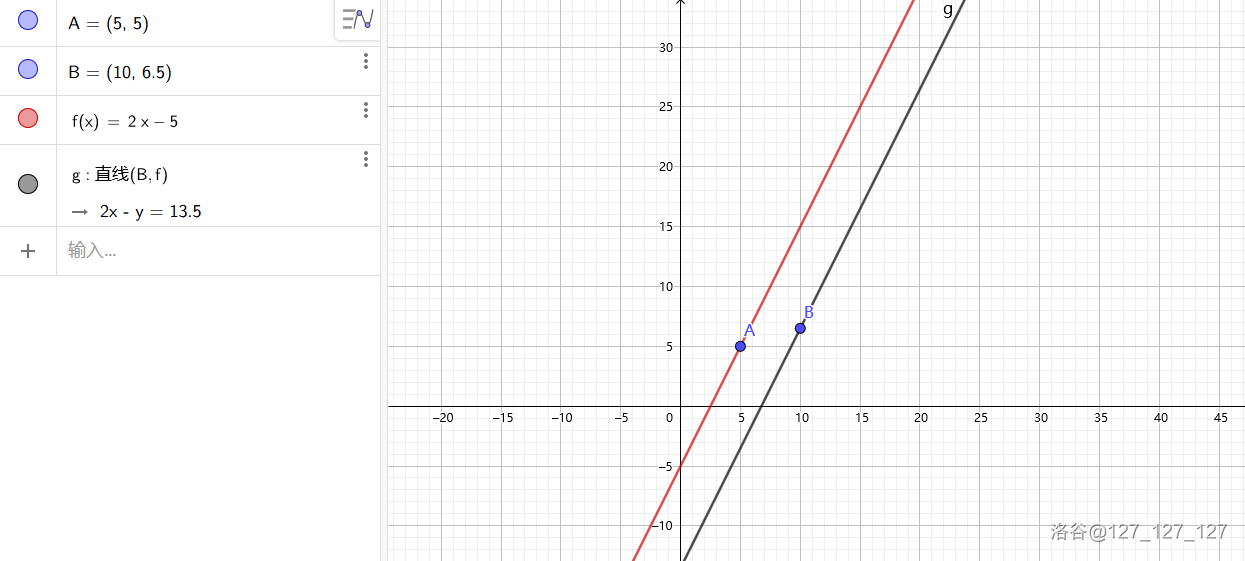
可以看到,无论怎样,斜率单调不降直线集合\(l_i,l_{i+1}...l_n\),平移至\(A\)的截距永远都比平移至\(B\)的截距要大,也就是说,\(dp_i,dp_{i+1}...dp_n\)在这个决策点上永远取不到最优答案,那么我们就可以\(pop\)掉这个点了。
再看队尾?
考虑加入当前决策\(i\)会出现的情况,

\(RT\),\(A\)为\(q_{t-1}\),\(B\)为\(q_t\),\(C\)为\(i\)。
当上图情况出现时,即直线\(AB\)的斜率\(\ge\) 直线\(BC\)的斜率,\(q_t\)不优。
我们看直线\(f\),这条直线表明了\(q_{t-1}\)还有救还能用,直线\(g\)表示\(i\)有用,自己yy 手玩 动脑筋想一下\(B\)绝不会被我们用到(因为在任意情况下\(A\)、\(C\)都至少有一点比\(B\)优),所以该点也可以\(pop\)掉。
整个\(dp\)过程:
\(for\ each\ i\ \in n\)
\(\ \ \ \ \ while(q.szie()>1\ and\ Slope(q_{h+1},\ q_h) \le S_i)\ h++\)
\(\ \ \ \ \ dp_i=...\)
\(\ \ \ \ \ while(q.szie()>1\ and\ Slope(q_{t-1},\ q_t) \ge Slope(q_t, i))\ t--\)
\(\ \ \ \ \ end\)
其中\(Slope(i,\ j)\)为斜率计算公式,有时为了精度问题,还会用交叉相乘。
\(\Large Ques:\)
\(\large \text {斜率优化的作用?}\)
当然是优化时间复杂度了,因为每个点最多入队一次,所以总时间复杂度是\(O(n)\)的。
课后作业:
P5785 P3195 CF311B P2120
\(\Large \text {多项式}\)
咕咕咕。
标签:Slope,直线,le,入门,多项式,斜率,ge,dp 来源: https://www.cnblogs.com/sizeof127/p/14614502.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
