标签:lfloor long 分块 数论 dfrac ll 笔记 rfloor sum
概念
我们考虑这样一个问题:求 \(\sum_{i=1}^{k} \lfloor \dfrac{n}{i} \rfloor\)
我们以 \(n=7,k=7\) 为例子,先画出 \(f(x) = \dfrac{7}{x} \ (1 \leq x \leq 7)\) 的图像
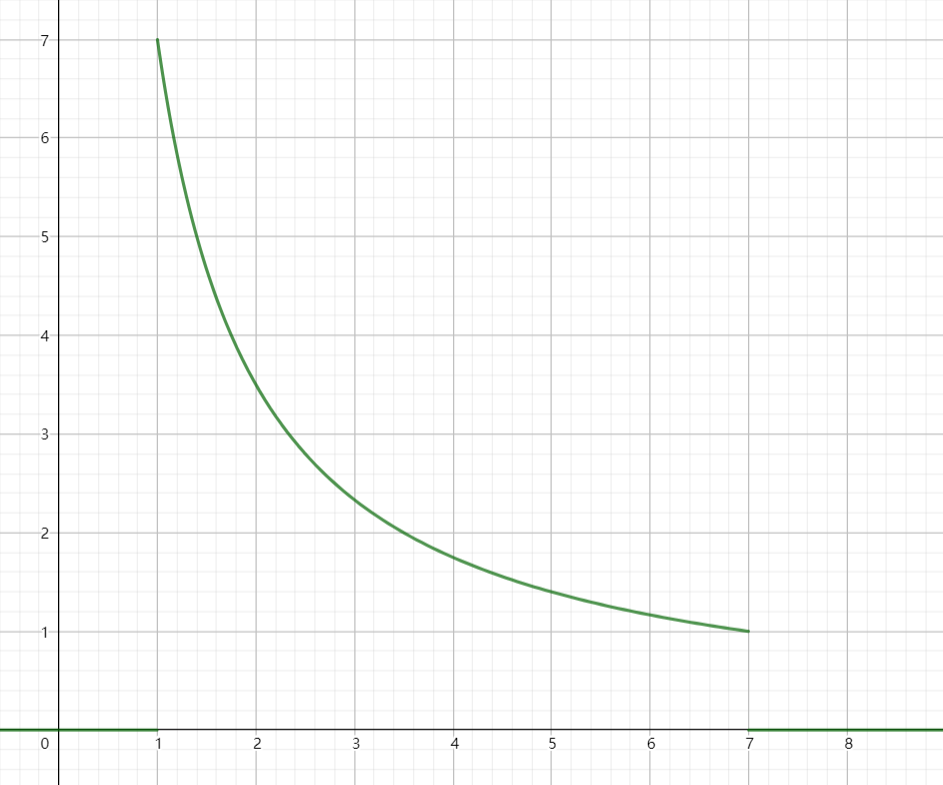
因为我们的取值是向下取整的,我们描出所有可能的取值
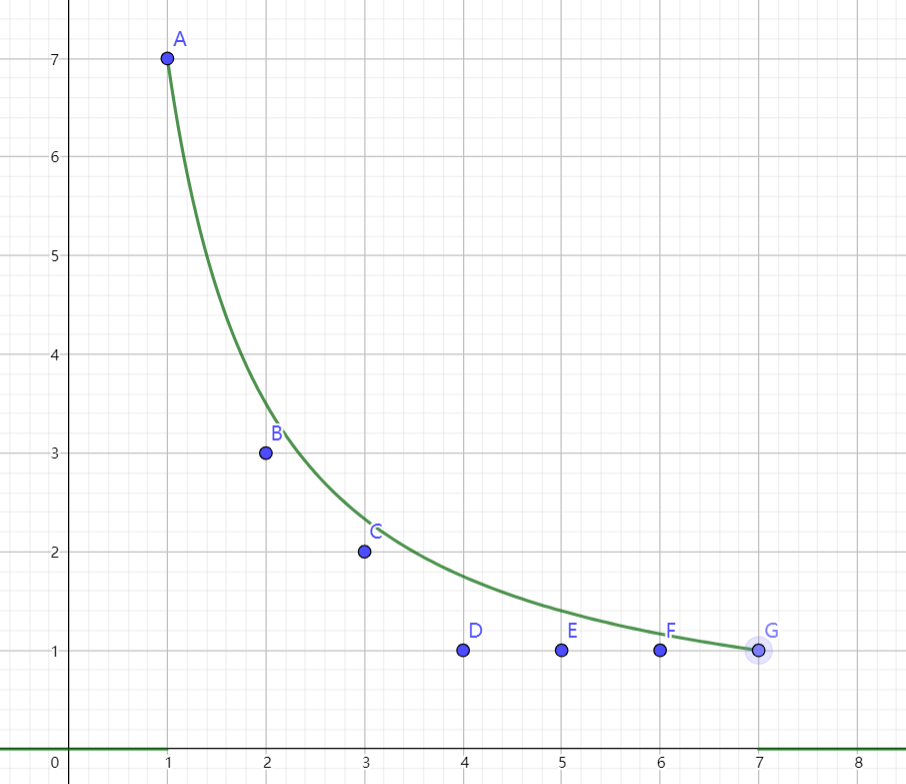
注意到所有的点按照取值可以分成若干段
我们可以一次性处理一个段的答案,把整段对答案的贡献加上即可
这就是数论分块
实现
如果要实现整块一起统计,我们需要求出每一块的块头 \(l\) 和块尾 \(r\),则:
\[Ans = \sum_{i=1}^{k} \lfloor \dfrac{n}{i} \rfloor = \sum_{[l,r]} (r-l+1)(\lfloor \dfrac{n}{l} \rfloor) \]注意到每一块的 \(l\) 都可以由上一块的 \(r\) 推出,故我们秩序讨论如何在已知 \(l\) 的情况下推出 \(r\)
令 \(t = \lfloor \dfrac{n}{l} \rfloor\) ,容易得到
\[\begin{cases} r = \min(\lfloor \dfrac{n}{t} \rfloor,n) \ \ \ &(t \neq 0) \\ r = n \ \ \ &(t=0) \end{cases} \]直接计算即可
应用
UVA11526 H(n)
模板题
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int T;
inline ll solve(ll n) {
ll res = 0;
for (ll l = 1, r; l <= n; l = r + 1) {
r = (n / l) ? min(n / (n / l), n) : n;
res += (n / l) * (r - l + 1);
}
return res;
}
signed main() {
scanf("%d", &T);
for (ll n; T; --T) {
scanf("%lld", &n);
printf("%lld\n", solve(n));
}
return 0;
}
P2261 [CQOI2007]余数求和
先推式子
\[\begin{aligned} G(n,k) &= \sum_{i=1}^{n} k \bmod i \\ &= \sum_{i=1}^{n} k - i \times \lfloor \dfrac{k}{i} \rfloor \\ &= nk - \sum_{i=1}^{n} i \times \lfloor \dfrac{k}{i} \rfloor \end{aligned} \]直接用数论分块解决即可
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n, k, res;
signed main() {
scanf("%lld%lld", &n, &k);
for (ll l = 1, r; l <= n; l = r + 1) {
r = (k / l) ? min(k / (k / l), n) : n;
res += (k / l) * ((l + r) * (r - l + 1) >> 1);
}
printf("%lld", n * k -res);
return 0;
}
P3935 Calculating
令 \(g(x) = \sum_{i=1}^{n} f(i)\) ,则
\[\sum_{i=l}^{r} = g(r) - g(l-1) \]我们推一下 \(g(x)\)
\[\begin{aligned} g(x) &= \sum_{i=1}^{x} f(i) \\ &= \sum_{i=1}^{x} \sum_{j=1}^{x} [i \mid j] \\ &= \sum_{i=1}^{x} \lfloor \dfrac{x}{i} \rfloor \end{aligned} \]直接用数论分块解决即可
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const ll Mod=998244353;
ll l, r;
inline ll g(ll n) {
ll res = 0;
for (ll l = 1, r; l <= n; l = r + 1) {
r = (n / l) ? min(n / (n / l), n) : n;
res = (res + (n / l) * (r - l + 1)) % Mod;
}
return res;
}
signed main() {
scanf("%lld%lld", &l, &r);
printf("%lld", ((g(r) - g(l - 1)) % Mod + Mod) % Mod);
return 0;
}
标签:lfloor,long,分块,数论,dfrac,ll,笔记,rfloor,sum 来源: https://www.cnblogs.com/wshcl/p/slfk.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
