拉格朗日插值
定义:
什么是插值?
百度百科上这样写:
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。 [1]
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
插值:用来填充图像变换时像素之间的空隙。
人看的确信
通俗点就是李云龙拉来了一门意大利炮,然后一炮打出去,那么轨迹就可以抽象为一个函数 \(f(t)\),然后因为炮弹飞的很快,你能看见部分轨迹上的点,那么插值就是让你通过这些点来近似还原函数。
拉格朗日插值法
插值有很多种求法:三角函数插值,线性插值,牛顿插值,拉格朗日插值。
思想就是硬凑确信。
怎么硬凑?假设平面上有三个点,\((x_1,y_2),(x_2,y_2),(x_3,y_3) \ \ x_1<x_2<x_3\)。
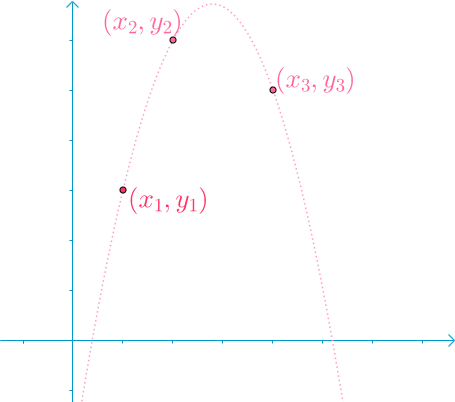
然后拉格朗日这个人呢就想对每个点搞一个子函数 \(f_i(x)\),强制令在 \(x=x_i\) 的时候 \(f_i(x)=1\),在\(x=x_j,j \ne i\) 的时候 \(f_i(x)=0\),然后把这 \(n\) 个子函数凑起来。
那怎么计算这 \(n\) 个子函数?我们设第 \(i\) 个子函数为:
\[f(x)=\begin{cases}0 \ \ x = x_j(j \ne i) \\1 \ \ x=x_j \end{cases} \]然后插值的结果就是:
\[f(x)= \sum_{i=1}^{n}y_if_i(x) \]现在好了,如何构造出子函数的形式呢?
因为在 \(x=x_j ,j\ne i\) 时要为 \(0\),我们可以想到令分子为 \(0\)。
因为在 \(x=x_i\) 时要为 \(1\),所以想到此时分子分母相同。
以 \(f_1(x)\) 举例,那就是:
\[f_1(x)=\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} \]这样就满足了条件。
那么求和就是:
\[f(x)= \dfrac{y_1(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+ \dfrac{y_2(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+ \dfrac{y_3(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} \]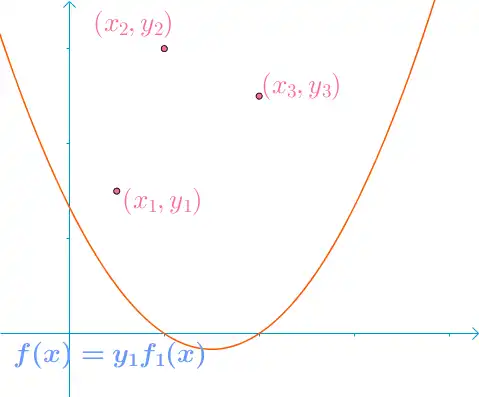
推广到一般,对于 \(n\) 个点,设:
\[f_i(x)=\dfrac{\prod_{j \ne i}(x-x_j)}{\prod_{j \ne i} (x_i-x_j)} \]那么插值结果就是:
\[f(x)=\sum_{i=1}^{n}y_if_i(x)=\sum_{i=1}^{n}y_i \times \dfrac{\prod_{j \ne i}(x-x_j)}{\prod_{j \ne i} (x_i-x_j)} \]#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define debug cout<<"Szt ak ioi\n";
#define int long long
const int Mod=998244353;
const int N=1e6+7,M=2e3+1;
using namespace std;
inline int read() {
int x=0,f=0;
char ch=getchar();
while(!isdigit(ch))f|=(ch=='-'),ch=getchar();
while(isdigit(ch))x=(x<<1)+(x<<3)+(ch&15),ch=getchar();
return f?-x:x;
}
int Ans,n,k,x[N],y[N];
int inv(int a,int b){
int res=1;while(b){if(b&1) res=(res*a)%Mod;
b>>=1;a=(a*a)%Mod;}return res;
}
signed main() {
n=read(),k=read();
for(int i=1;i<=n;i++)x[i]=read(),y[i]=read();
for(int i=1;i<=n;i++){
int Fz=y[i]%Mod,Fm=1;
for(int j=1;j<=n;j++){
if(i==j) continue;
Fz=((Fz*(k-x[j]))%Mod);
Fm=((Fm*(x[i]-x[j]))%Mod);
}Ans=(Ans+(Fz*inv(Fm,Mod-2)%Mod)+Mod)%Mod;
}
printf("%lld\n",(Ans+Mod)%Mod);
return 0;
}
重心拉格朗日
咕。
标签:拉格朗,函数,插值,dfrac,ne,prod 来源: https://www.cnblogs.com/BlackDan/p/16553363.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
