标签:begin right end matrix 元解 线性方程组 int 高斯消 left
初等行变换
矩阵的初等行变换是实现高斯消元的方法
初等行变换有三种
- 某一行所有数乘\(k(k ≠ 0)\)
- 交换某两行
- 将某一行加上另一行的若干倍
高斯消元
高斯消元有四种操作
- 找到绝对值最大的一行(为了代码的稳定性)
- 将该行移到最上面
- 将该行第一个数变为1
- 将最上面一行下面所有行的第\(c\)列变成0
以上四种操作均可通过初等行变换实现
判断解
取决于矩阵的形状
1. 完美阶梯形 —— 唯一解
每一个未知数对应一个常数,因此只有一个解
2. \(0 = k(k\neq 0)\) —— 无解
矩阵中有一个方程未知数的系数为0,而右侧的常数非0,则\(0 \neq 0\),无解
3. \(0=0\) —— 无数解
矩阵中有一个方程左右两侧都是0,则未知数可以取任意值,有无数解
想法
将原方程组化成矩阵,例如
\[\left\\{ \begin{matrix} x_{1} + 2x_{2} -x_{3} = -6\\\ 2x_{1} + x_{2} -3x_{3} = -9\\\ -x_{1} -x_{2} + 2x_{3} = 7 \\\ \end{matrix} \right. \]可以转化为
\[\left( \begin{matrix} 1 & 2 & -1 & -6\\\ 2 & 1 & -3 & -9\\\ -1 & -1 & 2 & 7 \\\ \end{matrix} \right) \]然后运用高斯消元进行变形,模拟:
第一次迭代
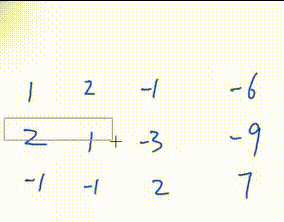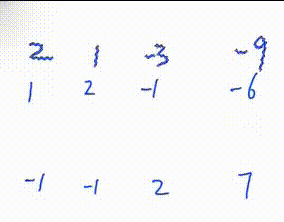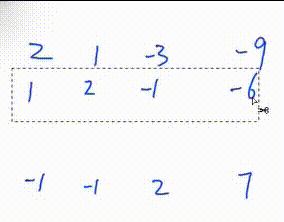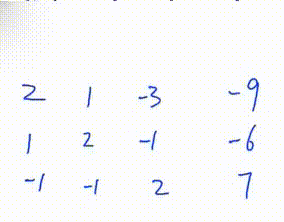
1. 找到绝对值最大的一行
2. 将该行移到最上面
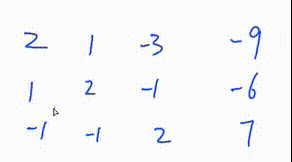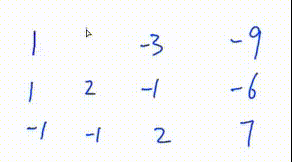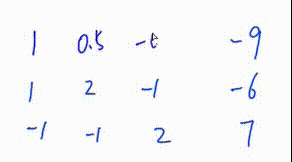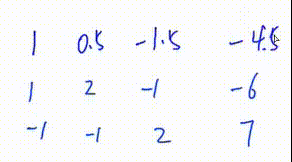
3. 将该行第一个数变为1
此处是将第一行所有数乘\(\frac12\)
初等行变换\(1.\)
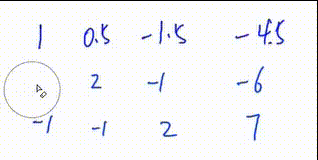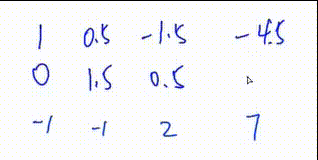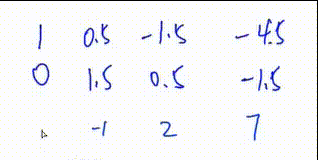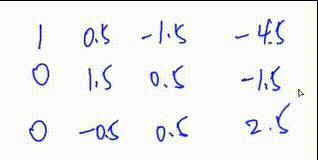
4.将第一行下面所有行的第\(c\)列变成0
此GIF中第一次操作 将第二行减去第一行的一倍
初等行变换\(3.\)
第二次操作 将第三行加上第一行的一倍
初等行变换\(3.\)
第二次迭代
注意:做完第一次迭代时,第一行就固定了,因此只需要从下面开始即可
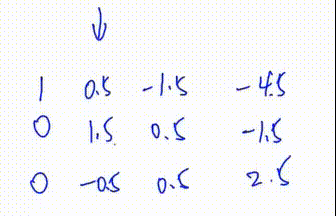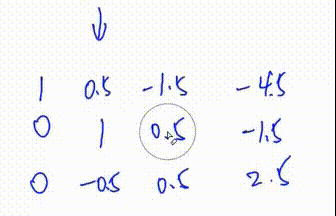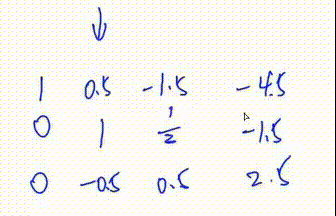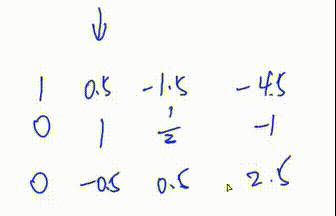
此处第三列y总笔误,应是\(\frac13\)而不是\(\frac12\)
1. 找到绝对值最大的一行
2. 将第二行行移到最上面此时第二行本身就符合1.2.的要求,因此不用动
3. 将第二行第一个数变为1
即 将第二行乘以\(\frac23\)
初等行变换\(1.\)
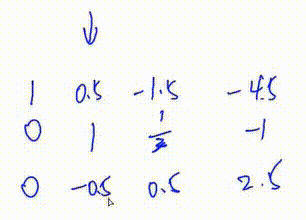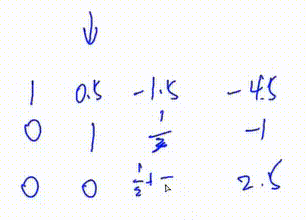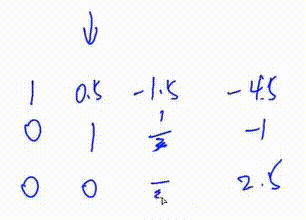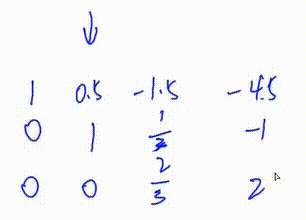
4.将第一行下面所有行的第\(c\)列变成0
此处将第三行加上\(\frac12\)倍的第二行
初等行变换\(3.\)
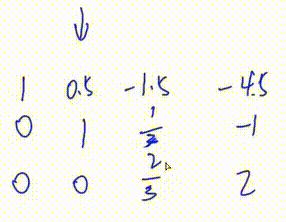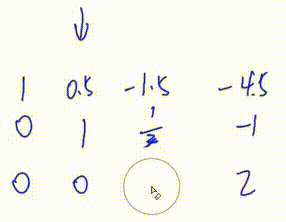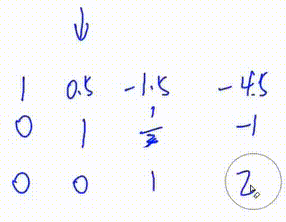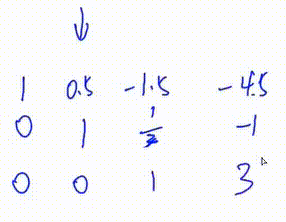
3. 将第三行第一个数变为1
即 将第三行乘以\(\frac32\)
解方程
我们发现这是一个完美的阶梯形矩阵,因此该方程组有唯一解
矩阵
化成方程组的形式:
\[\left\{ \begin{aligned} x_{1} + \frac12 x_{2} -\frac32 x_{3} &= -\frac92 \\\ x_{2} + \frac13 x_{3} &= -1\\\ x_{3} & = 3 \\\ \end{aligned} \right. \]我们发现\(x_3\)在消元的过程中已经解出来了,要解②就只需要将\(③\times \frac13\)得
\(\frac13 = 1④\)
然后用\(②-④\),得:
即
\[\left( \begin{matrix} 1 & \frac12 & -\frac32 & -\frac92\\\ 0 & 1 & 0 & -2\\\ 0 & 0 & 1 & 3 \\\ \end{matrix} \right) \]对①进行同样的操作,解得
\[\left\{ \begin{aligned} x_{1} -\frac32 x_{3} &= -\frac{7}{2} \\\ x_{2} &= -2\\\ x_{3} & = 3 \\\ \end{aligned} \right. \]\[\left( \begin{matrix} 1 & 0 & -\frac32 & -\frac{7}{2}\\\ 0 & 1 & 0 & -2\\\ 0 & 0 & 1 & 3 \\\ \end{matrix} \right) \]再消去\(x_3\):
\[\left\{ \begin{aligned} x_{1} &= 1 \\\ x_{2} &= -2\\\ x_{3} & = 3 \\\ \end{aligned} \right. \]也就是
\[\left( \begin{matrix} 1 & 0 & 0 & 1\\\ 0 & 1 & 0 & -2\\\ 0 & 0 & 1 & 3 \\\ \end{matrix} \right) \]码来!
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath> // fabs() = float abs = 浮点数的绝对值,相对应的,整数的绝对值即为abs()
using namespace std;
const int N = 110;
const double eps = 1e-8; // 防止出现精度问题
double a[N][N];
int n;
int gauss()
{
int c = 0, r = 0;
for(; c < n; c++)
{
int t = r;
for (int i = r; i < n; i ++ ) // 第一步,找绝对值最大的行
{
if(fabs(a[i][c]) > fabs(a[t][c]))
t = i;
}
if(fabs(a[t][c]) < eps) continue; // 代表这一列已经被处理过了
for(int i = c; i <= n; i++) // 第二步
swap(a[t][i], a[r][i]); // 将这一行调到最上面
for(int i = n; i >= c; i--) // 第三步
a[r][i] /= a[r][c]; // 要倒着算,否则会影响后面的数
for(int i = r + 1; i < n; i++) // 第四步
{
if(fabs(a[i][c]) > eps) // 如果是0就不用操作了
{
for(int j = n; j >= c; j--)
{
a[i][j] -= a[r][j] * a[i][c];
}
}
}
r++;
}
if(r < n) // 方程数 < n
{
for(int i = r; i < n; i++)
{
if(fabs(a[i][n]) > eps) // 0 != 0
{
return 2; // 无解
}
}
return 1; // 无数解, 0=0
}
for(int i = n - 1; i >= 0; i --) // 有解从下往上回代
{
for(int j = i + 1; j < n; j++)
{
a[i][n] -= a[i][j] * a[j][n];
}
}
return 0;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n + 1; j ++ )
scanf("%lf", &a[i][j]);
int t = gauss();
if(t == 0) // 有唯一解
{
for (int i = 0; i < n; i ++ )
{
if(fabs(a[i][n]) < eps) a[i][n] = 0.00; // 避免输出-0.00
printf("%.2lf\n", a[i][n]);
}
}
else if(t == 1) puts("Infinite group solutions"); // 无数解
else puts("No solution"); // 无解
}
标签:begin,right,end,matrix,元解,线性方程组,int,高斯消,left 来源: https://www.cnblogs.com/MoyouSayuki/p/16513725.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
