标签:约束条件 geq 可行 变量 单纯形法 线性规划 vdots
单纯形法
线性规划一般形式
在约束条件下、寻找目标函数 z 的最大值
\[max(or \ min) \ z = \displaystyle\sum_{j=1}^n c_jx_j \\ s.t. \begin{cases} \displaystyle\sum_{j=1}^n a_{ij}\ \leq\ (or\ =,\geq)\ b_i\quad(i\ = 1,...,m) \\ \\ x_j\ \geq \ 0 \qquad \qquad \qquad \quad \ \ \ (j\ = 1,...,n) \end{cases} \]线性规划的标准形式
标准形需要满足的条件:
- 目标函数求最大值 max
- 约束条件均为等式
- 所有决策变量均为非负约束
- 约束条件右端常数项 \(b_i\) 全为非负值
一般来说,规定线性规划的标准形式为:
\[max\ z = \displaystyle\sum_{j=1}^n c_jx_j \\ s.t. \begin{cases} \displaystyle\sum_{j=1}^n a_{ij}\ =\ b_i\qquad \qquad(i\ = 1,...,m) \\ \\ x_j\ \geq \ 0\ ,\ b_i\ \geq \ 0 \qquad (j\ = 1,...,n) \end{cases} \]可以写成矩阵形式:
\[max\ z\ = CX \\ AX\ =\ b \\ X\ \geq \ 0 \\ A\ =\ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \]将一般线性规划问题化为标准型:
- 目标函数极大化。(可通过取相反数实现)
- 将不等式约束条件通过添加松弛变量得到方法华为等式
- 约束条件为 \(\leq\) 不等式,则在约束条件的左端加上一个非负的松弛变量;
- 约束条件为 \(\geq\) 不等式,则在约束条件的左端减去一个非负的松弛变量。
- 取值无约束的变量:
- 若存在无约束的变量\(x_k\),可令 \(x_k\ = x_k^{'}\ -\ x_k^{''}\),其中 \(x_k^{'},x_k^{''}\ \ge \ 0\)。
单纯形法求解
几个基本定理:
- 若线性规划问题存在可行解,则问题的可行域是凸集
- 引理:线性规划问题的可行解 \(X\ =\ (x_1,\cdots,x_n)^{T}\) 为基可行解的充要条件是 \(X\) 的正分量所对应的系数列向量是线性无关的。
- 线性规划问题的基可行解 \(X\) 对应线性规划问题可行域(凸集)的顶点
- 若线性规划问题有最优解一定存在一个基可行解是最优解
单纯形法求解过程:
- 化为标准型(要求 \(b \ge 0\)),确定初始基B,建立初始单纯行表(假设A矩阵中存在单位矩阵)
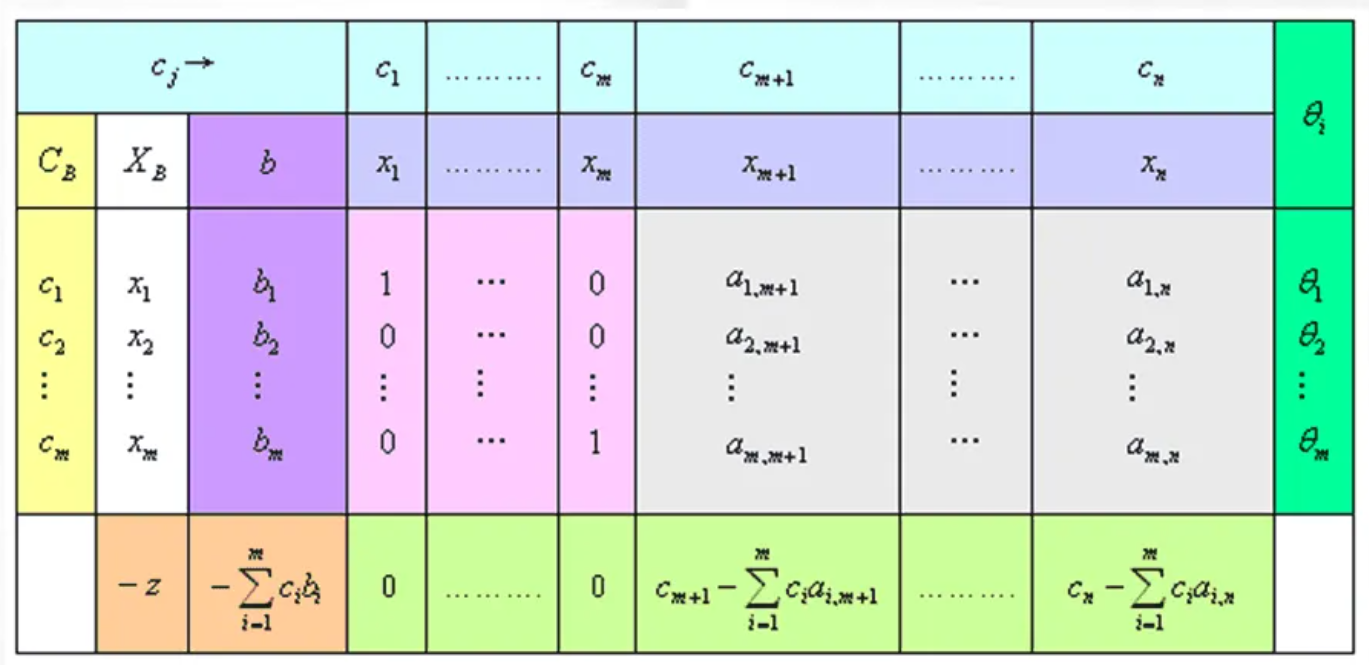
- 其中:
- 若 \(\sigma_j\ \le 0\ (j\ =\ m+1,\cdots,n)\),则已得到最优解,否则转入下一步
- 若在 \(j\ =\ m+1,\cdots,n\) 中,存在 \(\sigma_k\ >\ 0\), 而 \(P_k\ <\ 0\),则无最优解。
- 确定换入变量和换出变量
- 由 \(\max(\sigma_k>0)\ =\ \sigma_k\),确定 \(x_k\) 为换入变量
- 由 $$\theta\ =\ \min{(\frac{b_i}{a_{ik}}\ |\ a_{ik}\ >\ 0)}\ = \frac{b_l}{a_{lk}}$$ 确定 \(x_l\) 为换出变量。
- 以 \(a_{lk}\) 为主元进行迭代
即将\[P_k= \begin{pmatrix} a_{1k} \\ \vdots \\ a_{lk} \\ \vdots \\ a_{mk} \end{pmatrix} 迭代成 \begin{pmatrix} 0 \\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \to l行 \] - 重复 2~5 步骤
单纯形法进一步讨论
- 人工变量法(大M法)
- 凑单位矩阵添加人工变量
- 目标函数中人工变量的系数为足够大的一个负值,用“\(-M\)”表示
- 两阶段法
- 第一阶段实现求解一个目标函数中只包含人工变量的线性规划问题(令目标函数中其他变量的系数取零),人工变量的系数取某个正的常数(一般取1),在保持原问题约束条件不变的情况下求这个目标函数的极小值
- 当人工变量取值为0时,目标函数值也为0,这时的最优解就是原线性规划问题的的一个可行解
- 如果第一阶段求解结果表明最优解的目标函数值不为0,即最优解的基变量中含有人工变量,则表明原线性规划问题无可行解
- 第一阶段表明问题有可行解时,第二阶段从第一阶段的最终单纯形表出发,去掉人工变量,并按问题原来的目标函数,继续寻找问题的最优解
- 第一阶段实现求解一个目标函数中只包含人工变量的线性规划问题(令目标函数中其他变量的系数取零),人工变量的系数取某个正的常数(一般取1),在保持原问题约束条件不变的情况下求这个目标函数的极小值
标签:约束条件,geq,可行,变量,单纯形法,线性规划,vdots 来源: https://www.cnblogs.com/wendaidai/p/16417573.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
