标签：frac 数的几何 意义 切线 曲线 2x quad underline

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【高分突破系列】2021-2022学年高二数学下学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

选择性必修第二册同步拔高，难度3颗星！

模块导图

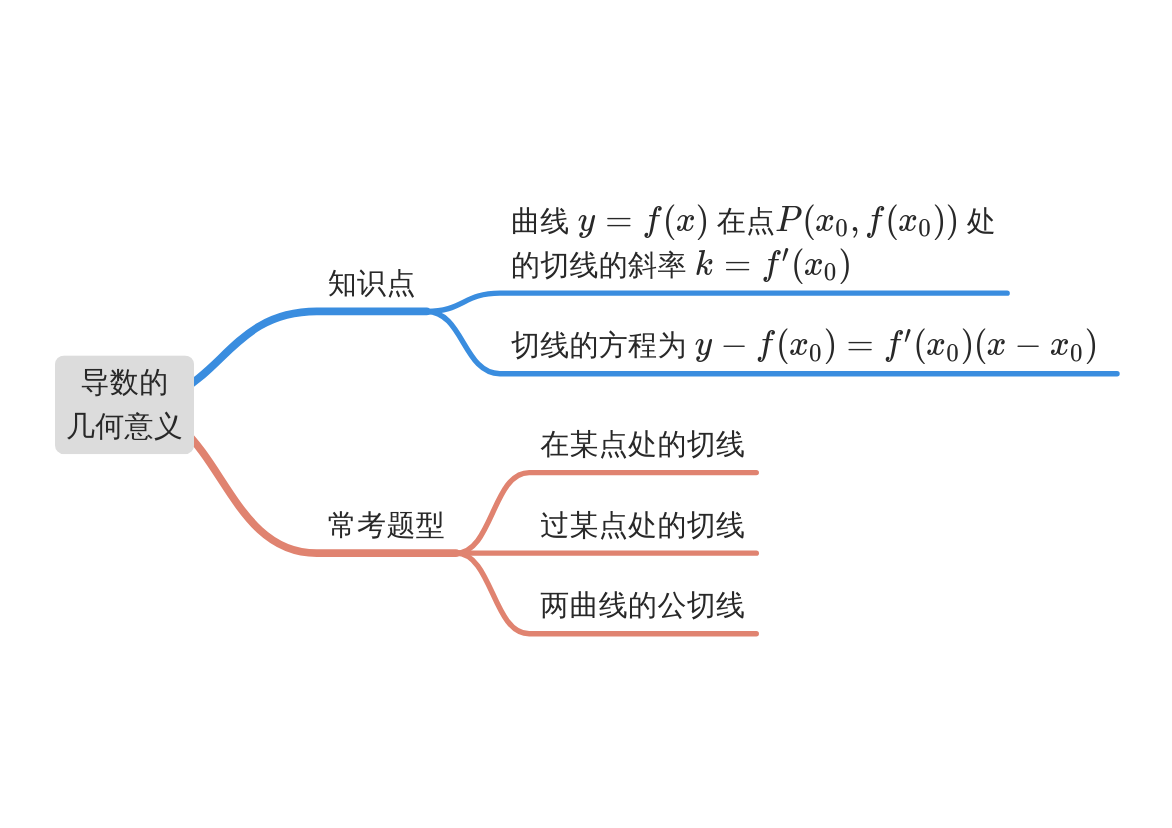
知识剖析

导数的几何意义

函数\(y=f(x)\)在点\(x=x_0\)处的导数的几何意义是曲线\(y=f(x)\)在点\(P(x_0 ,f(x_0))\)处的切线的斜率，即：曲线\(y=f(x)\)在点\(P(x_0 ,f(x_0))\)处的切线l的斜率\(k=f'(x_0)\)，
切线l的方程为\(y-f(x_0)=f'(x_0)(x-x_0)\)．

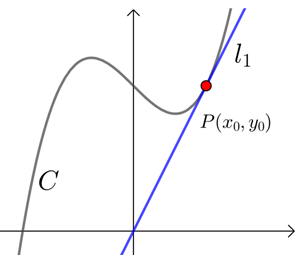
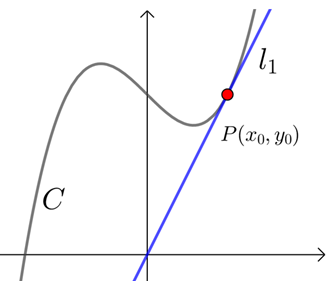
"过点\(x=x_0\)”与"在点\(x=x_0\)处"的区别

曲线\(C：y=f(x)\)在点\(P(x_0 ,y_0)\)处的切线指的是\(P\)为切点的切线，如图一；
过点\(P(x_0 ,y_0)\)的切线是指切线过点\(P\)，点\(P\)是否切点均可，切线可多条，如图二.

经典例题

【题型一】在某点处的切线

【典题1】 函数\(y=f(x)\)的图象如图所示，\(f'(x)\)是函数\(f(x)\)的导函数，下列数值排序正确的是(　　)

A．\(f^ {\prime}(2)<f^{\prime} (6)<f(6)-f(2)<0\)
B．\(f^{\prime}(6)<f^{\prime}(2)<f(6)-f(2)<0\)
C．\(f(6)-f(2)<f^{\prime} (6)<f^{\prime}(2)<0\)
D．\(f^{\prime} (2)<f(6)-f(2)<f^{\prime}(6)<0\)
【解析】根据题意，设\(M(2 ,f(2))\)、\(N(6,f(6))\)为函数的上的点，
则\(f'(2)\)为函数\(f(x)\)在\(x=2\)处切线的斜率\(k_1\)，
\(f^{\prime}(6)\)为函数\(f(x)\)在\(x=6\)处切线的斜率\(k_2\)，
\(f(6)-f(2)=\frac{f(6)-f(2)}{3-2}\)为直线\(MN\)的斜率\(k_3\)，
结合图象分析可得\(k_1<k_3<k_2<0\)，
即\(f^{\prime} (2)<f(6)-f(2)<f^{\prime}(6)<0\)；
故选：\(D\)．

【点拨】\(k=tanα\)，直线越靠近\(y\)轴，斜率\(|k|\)越大.

【典题2】 若直线\(y=x\)是曲线\(f(x)=x^3-3x^2+ax\)的切线，则\(a=\)\(\underline{\quad \quad}\)．
【解析】依题意得\(f^{\prime}(x)=3x^2-6x+a\)
设切点\(P(x_0 ,y_0)\)
则由导数的几何意义可得 \(f^{\prime}(x_0 )=1⇒3x_0^2-6x_0+a=1\) ①
\(∵\)点P在切线\(y=x\)上 \(∴y_0=x_0\) ②
\(∵\)点\(P\)在曲线上 \(∴y_0=x_0^3－3x_0^2+ax_0\) ③
由①，②, ③联立得\(\left\{\begin{array}{l} 3 x_{0}^{2}-6 x_{0}+a=1 \\ y_{0}=x_{0} \\ y_{0}=x_{0}^{3}-3 x_{0}^{2}+a x_{0} \end{array}\right.\)，
解得\(a=1\)或\(\frac{13}{4}\)
\(∴a\)的值为\(1\)或\(\frac{13}{4}\)．
【点拨】由于本题不知道切点，由待定系数法的想法，设切点\(P(x_0 ,y_0)\)，它即在切线上又在曲线上，又由导数的几何意义得到了关于\(x_0 ,y_0 ,a\)的方程组！

【典题3】 已知\(M(1 ,0)\)，\(N\)是曲线\(y=e^x\)上一点，则\(|MN|\)的最小值为\(\underline{\quad \quad}\) .
【解析】\(y=e^x\)的导数为\(y'=e^x\)．
设\(N(m ,e^m)\)，可得过\(N\)的切线的斜率为\(e^m\)，
当\(MN\)垂直于切线时，\(|MN|\)取得最小值，
可得\(\frac{e^{m}}{m-1} \cdot e^{m}=-1\)，即\(e^{2m}+m-1=0\)，
因为\(f(x)=e^{2x}+x-1\)单调递增，且\(f(0)=0\)，
所以\(m=0\)，即\(N(0 ,1)\)，
所以\(|MN|\)的最小值为\(\sqrt2\)．

【点拨】当\(MN\)垂直切线时，\(|MN|\)取得最小值；如图，\(MN≤MA≤MN_1\).

巩固练习

1(★)已知函数\(f(x)\)在\(R\)上可导，其部分图象如图所示，设\(k=\frac{f\left(x_{1}\right)-f\left(x_{2}\right)}{x_{1}-x_{2}}\)，则下列不等式正确的是(　　)

A．\(k<f'(x_1)<f'(x_2)\)
B．\(f'(x_1)<k<f'(x_2)\)
C．\(f'(x_2)<f'(x_1)<k\)
D．\(f'(x_1)<f'(x_2)<k\)
2(★)曲线\(y=x^3+lnx+1\)在点\((1 ,2)\)处的切线方程为\(\underline{\quad \quad}\)．

3(★★)曲线\(y=lnx-\frac{1}{x}\)在\(x=1\)处的切线的倾斜角为\(α\)，则\(sin2α=\)\(\underline{\quad \quad}\)．

4(★★★)已知函数\(y=e^x\)的图象在点\((a_k ,e^{a_k})\)处的切线与\(x\)轴的交点的横坐标为\(a_{k+1}\)，其中\(k∈N^*\)，\(a_1=0\)，则\(a_1+a_3+a_5=\)\(\underline{\quad \quad}\)．

5(★★★)若函数\(f(x)=ax+sinx\)的图象上存在互相垂直的切线，则实数\(a\)的值为\(\underline{\quad \quad}\)．

答案

1. \(B\)
2. \(4x－y－2=0\)
3. \(\frac{4}{5}\)
4. \(-6\)
5. \(0\)

【题型二】过某点处的切线

【典题1】 已知曲线\(f(x)=2x^3+4\)，曲线过点\(P(-1 ,2)\)的切线方程.
【解析】\(∵f(x)=2x^3+4\) \(∴f^{\prime}(x)=6x^2\)
设切点为\((x_0 ,2x_0^3+4)\)，则切线斜率\(k=f^{\prime}(x_0 )=6x_0^2\)，
切线方程为\(y-(2x_0^3+4)=6x_0^2 (x-x_0 )\)\(⟹y=6x_0^2 x-4x_0^3+4\)
\(∵\)切线过点\(P(－1 ,2)\)
\(∴-6x_0^2-4x_0^3+4=2\)\(⇒2x_0^3+3x_0^2-1=0\)
解得\(x_0=-1\)或\(\frac{1}{2}\)，
则切线方程为\(y=6x+8\)或\(y=\frac{3}{2}x+\frac{7}{2}\).
【点拨】
① 本题点\(P(-1 ,2)\)不一定是切点，故可先设切点\((x_0 ,2x_0^3+4)\)，利用“在某点处的切线”方法求出含参数\(x_0\)的切线方程，再把点\(P\)代入求出\(x_0\)，进而容易得到切线方程;
② 如何求解方程\(2x_0^3+3x_0^2-1=0\)？
\({\color{Red}{ 方法一 \quad 拆项分组因式分解}}\)
\(2x_0^3+3x_0^2-1=0\)
\(⇒3x_0^3+3x_0^2-(1+x_0^3 )=0\)\(⇒3x_0^2 (x_0+1)-(x_0+1)(x_0^2-x_0+1)=0\)\(⇒ (x_0+1)(2x_0^2-x_0-1)=0\)
\(⇒ (x_0+1)^2 (2x_0-1)=0\)
\(⇒x_0=-1\)或\(x_0=\frac{1}{2}\)
\({\color{Red}{ 方法二 \quad 待定系数法}}\)
先由方程特点猜出有一个解是\(x_0=-1\),则可知\(x_0+1\)是\(2x_0^3+3x_0^2-1\)的因式，
设\(2x_0^3+3x_0^2-1=(x_0+1)(2x_0+mx_0-1)\)，把右式展开易得\(m=-1\)，
则\(2x_0^3+3x_0^2-1=(x_0+1)(2x_0^2-x_0-1)\)\(=(x_0+1)^2 (2x_0-1)\)
\(∴x_0=-1\)或\(x_0=\frac{1}{2}\)

【典题2】 若过点\(P(－1 ,m)\)可以作三条直线与曲线\(C:y=xe^x\)相切，则\(m\)的取值范围是\(\underline{\quad \quad}\).
【解析】\(y^{\prime}=(x+1) e^x\)
设切点为\((x_0 ,x_0 e^{x_0})\)，
过点\(P\)的切线方程为\(y=\left(x_{0}+1\right) e^{x_{0}}\left(x-x_{0}\right)+x_{0} e^{x_{0}}\)，
代入点\(P\)坐标化简为\(m=\left(-x_{0}^{2}-x_{0}-1\right) e^{x_{0}}\)，
即这个方程有三个不等根即可，
令\(f(x)=(-x^2-x-1) e^x\)，
求导得到\(f^{\prime}(x)=(-x-1)(x+2) e^x\)，
函数在\((-∞ ,-2)\)上单调递减，在\((-2 ,-1)\)上单调递增，在\((-1 ,+∞)\)上单调递减，
故得到\(f(-2)<m<f(-1)\)\(\Rightarrow-\frac{3}{e^{2}}<m<-\frac{1}{e}\)
答案为\((-\frac{3}{e^{2}},-\frac{1}{e})\).
【点拨】过某点作曲线的切线可以有多条，先求在曲线上一点处的切线方程，把问题转化为方程解的个数.

巩固练习

1(★★)已知曲线\(y=lnx\)的切线过原点，则此切线的斜率为\(\underline{\quad \quad}\).

2(★★)过点\(A(2 ,1)\)做曲线\(f(x)=x^3－3x\)的切线，最多有\(\underline{\quad \quad}\)条.

3(★★)已知曲线\(f(x)=4x^2\)的一条切线经过点\((0 ,－1)\)，求该切线方程．

4(★★)已知函数\(f(x)=x^3－4x^2+5x－4\)，求经过点\(A(2 ,－2)\)的曲线\(f(x)\)的切线方程．

答案

1. \(\frac{1}{e}\)
2. \(3\)
3. \(y=2x-1\)或\(y=-2x-1\)
4. \(y+2=0\)或\(x-y-4=0\)

【题型三】两曲线的公切线

【典题1】 若直线\(y=kx+b\)是曲线\(y=e^{x-2}\)的切线，也是曲线\(y=e^x-1\)的切线，则\(b=\)\(\underline{\quad \quad}\)．
【解析】设直线\(y=kx+b\)与\(y=e^{x-2}\)和\(y=e^x－1\)的切点分别为\((x_1 ,e^{x_1-2})\)和\((x_2 ,e^{x_2}-1)\)，
则切线分别为\(y-e^{x_1-2}=e^{x_1-2} (x-x_1)\)，\(y-e^{x_2}+1=e^{x_2} (x-x_2)\)
化简得：\(y=e^{x_1-2} x+e^{x_1-2}-x_1 e^{x_1-2}\)，\(y=e^{x_2} x+e^{x_2}-1-x_2 e^{x_2}\)
依题意有：\(\left\{\begin{array}{l} e^{x_{1}-2}=e^{x_{2}} & (1)\\ e^{x_{1}-2}-x_{1} e^{x_{1}-2}=e^{x_{2}}-1-x_{2} e^{x_{2}} & (2) \end{array}\right.\)，
由方程①得\(x_1=2+x_2\)，代入方程②解得\(x_2=－ln2\)，
则\(b=e^{x_{2}}-1-x_{2} e^{x_{2}}=\frac{1}{2} \ln 2-\frac{1}{2}\)．
故答案为：\(\frac{1}{2} \ln 2-\frac{1}{2}\)．
【点拨】先分别求出两条切线，由于是公切线，所以它们是同一直线，两切线的斜率和\(y\)轴上的截距相等.

【典题2】 若曲线 \(C_1:y=x^2\)与曲线\(C_2:y=ae^x (a≠0)\)存在公共切线，则\(a\)的取值范围为\(\underline{\quad \quad}\)．
【解析】\(y=x^2\)在点\((m ,m^2)\)的切线斜率为\(2m\)，
切线方程为\(y=2m(x-m)+m^2=2mx-m^2\);
\(y=ae^x\)在点\((n ,ae^n)\)的切线斜率为\(ae^n\)，
切线方程为\(y=ae^n x+a(1-n)e^n\);
如果两个曲线存在公共切线，那么两切线相同，
则有\(\left\{\begin{array}{l} 2 m=a e^{n} & (1) \\ -m^{2}=a(1-n) e^{n}&(2) \end{array}\right.\)，
\(∵a≠0\)，\(∴m≠0\)，
由②÷①得\(-m=2(1-n)\)，即\(m=2n-2\)，
代入\(2m=ae^n\)得\(4n－4=ae^n (*)\)，
存在公共切线，等价于方程\((*)\)有解，
由\(y=4x－4\) ,\(y=ae^x\)的图象有交点即可．
设它们相切，切点为\(P(s ,t)\)，
则\(ae^s=4\)，且\(t=4s－4=ae^s\)，
解得\(s=2,t=4\)，\(a=\frac{4}{e^2}\) ，
由图易得要满足题意\(a≤\frac{4}{e^2}\)，
又\(a≠0\)，
故答案为\((-∞ ,0)∪(0 ,\frac{4}{e^2}]\)．
【点拨】得到”\(4n－4=ae^n\)有解"，可用分离参数法转化为\(a=\frac{4 n-4}{e^{n}}\)有解，
即\(y=a\)与\(f(x)=\frac{4 x-4}{e^{x}}\)有交点，从而转化为求函数的\(f(x)=\frac{4 x-4}{e^{x}}\)的值域；
\(\because f^{\prime}(x)=\frac{8 x-4}{e^{x}}\)
\(∴f(x)\)在\((-∞ ,2)\)递增，在\((2 ,+∞)\)递减，\(∴f(x)≤f(2)=\frac{4}{e^2}\)
\(∴a≤\frac{4}{e^2}\) 且\(a≠0\).

巩固练习

1(★★)已知曲线\(f(x)=xlnx\)在点\((e ,f(e))\)处的切线与曲线\(y=x^2+a\)相切，则\(a=\)\(\underline{\quad \quad}\)．

2(★★)若存在过点\((1 ,0)\)的直线与曲线\(y=x^3\)和\(y=ax^2+\frac{15}{4} x－9\)都相切，则实数\(a=\)\(\underline{\quad \quad}\)．

3(★★★)若二次函数\(f(x)=x^2+1\)的图象与曲线\(C:g(x)=ae^x+1(a>0)\)存在公共切线，则实数\(a\)的取值范围为\(\underline{\quad \quad}\)．

4(★★★)若曲线\(y=x^2\)与\(y=alnx(a≠0)\)存在公共切线，则实数\(a\)的取值范围是\(\underline{\quad \quad}\)．

答案

1. \(1－e\)
2. \(a=-\frac{25}{64}\)或\(－1\)
3. \((0 ,\frac{4}{e^2} ]\)
4. \((－∞ ,0)∪(0 ,2e]\)

标签：frac,数的几何,意义,切线,曲线,2x,quad,underline
来源： https://www.cnblogs.com/zhgmaths/p/15925905.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。