标签：given 嵌入 paradox list 社会科学 dict 悖论 节点 friend

学习资源来自，一个哲学学生的计算机作业 (karenlyu21.github.io)

---

1、背景问题

“网络”由节点组成，节点之间可能有边相连。网络常常是对社会的一种有效抽象，节点代表社会中的行动者，边代表行动者之间的联系。我们可以用一个矩阵（称为邻接矩阵）来表示网络，在程序中一般就是对应一个二维数组。邻接矩阵在(i,j)的值，表示i与j之间边的权重。一种基本的情形是权重为0或1，0表示有边，1表示没有边。此时的网络也称“图”。例如：

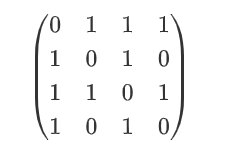
这个矩阵就表示如下一个网络（或图），节点符合A,B,C,D,分别对应矩阵的1,2,3,4列和行。

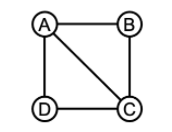
一个节点与自己总是没有边的，因此，矩阵从左上到右下的对角线上都是0。对于一个无向图，邻接矩阵A(i,j)=A(j,i)，即这一矩阵是对称的，以从左上到右下的对角线为轴。

基于图的邻接矩阵，我们可以通过计算得到对应社会网络的一些结构信息。例如，把一行内的值相加，就可以得到，该行对应的人有多少朋友。另一个例子是矩阵的乘幂，例如A²(i,j)表示节点i和j之间的长度为2的路径一共有多少条，也可以解释为i和j的共同朋友的个数。

利用这些计算操作，我们可以对网络的性质做出分析，这可以用以检验和社会网络相关的理论假设。作业“聚集系数和嵌入性”就是网络分析的一个例子。另一个作业则检验了社会网络学说的一个理论假设，即“友谊悖论”。

2、计算实践

2.1、聚集系数与嵌入性

2.1.1、作业描述与算法思路

本次作业的主要任务是计算某一社会网络中，每个节点的聚集系数，以及每条边的嵌入性。

在一个网络中，不同人的社交密度或强度（intensity）不一样，有的人把自己的朋友聚集起来的能力很强——ta的朋友往往互相之间也认识。我们用“聚集系数”来刻画这一现象。节点i的聚集系数指的是，i的朋友们中，两两之间也是朋友的概率。

计算聚集系数的基本思路如下：

先分析邻接矩阵，用一个字典变量friend_dict存储“谁是谁的朋友”，字典的键（key）i指的是节点i∈[0,n)，节点i的朋友j,k,…∈[0,n)被存储在该键对应的值（value）里（值是一个列表）。接着，我再两两分析节点i的朋友（我把他们俩称为以节点i为中介的“间接朋友”），用friend_dict存储的信息验证，他们俩是否为“直接朋友”。节点i的聚集系数就是“直接朋友”和“间接朋友”的比值。

两个人之间的关系也有性质上的差别，有的关系深深嵌入了周围的社交圈中——不仅他们俩是朋友关系，而且他们俩的共同好友很多。我们用“嵌入性”来刻画这一现象。边(i,j)的嵌入性，指的是节点i与j的共同朋友数。

计算嵌入性的基本思路如下：

分析网络中的边。对于边(i,j)，检查，节点i的朋友有多少也是节点j的朋友，这一过程也是用friend_dict完成的。

2.1.2、编程实现与要点说明

提前说明：笔者在原文中未给出net3.txt，故可自行给出，这里本人直接照抄背景问题中的矩阵。。。

首先，我们读取样本数据文件，把文件里的矩阵数据存储在一个numpy 2d-array A里。

import numpy as np

def arrayGen(filename):
    f = open(filename, 'r')
    r_list = f.readlines()  # 返回包含size行的列表, size未指定则返回全部行
    f.close()
    A = []
    for line in r_list:
        if line == '\n':
            continue
        line = line.strip('\n')
        line = line.strip()  # 用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列，不能删除中间字符
        row_list = line.split()  # 通过指定分隔符对字符串进行切片
        for k in range(len(row_list)):
            row_list[k] = row_list[k].strip()
            row_list[k] = int(row_list[k])
        A.append(row_list)  # 用于在列表末尾添加新的对象
    n = len(A[0])
    A = np.array(A)
    return A, n

filename = input('请输入邻接矩阵文件名：')  # 将邻居矩阵net3.txt放在同一文件夹下即可
A, n = arrayGen(filename)

分析这一网络，我们把“谁是谁的朋友”存储在一个字典变量friend_dict里，字典的键（key）N∈[0,n)是节点，节点i∈[0,n)的朋友被存储在该键对应的值（value）里。

friend_dict = {}
for i in range(n):
    friend_dict[i] = []
    for j in range(n):
        if A[i][j] ==1:
            friend_dict[i].append(j)

接着，我再两两分析节点i的朋友（他们俩是“间接朋友”，以节点i为中介），用friend_dict存储的信息验证，他们俩是否为“直接朋友”。以节点i为中介的间接朋友数存储在变量PossTriCl里，这些人中的直接朋友数存储在变量TriCl里。聚集系数ClCo=TriClPoss/TriCl。每一节点的聚集系数被存储在一个字典变量ClCo_dict里。

ClCo_dict = {}  # ClCo --> clustering coefficient
for(person, friend_list) in friend_dict.items():  # 以列表返回视图对象，是一个可遍历的key/value 对
    TriCl = 0  # 直接朋友
    for x in range(len(friend_list)):
        friend1 = friend_list[x]
        for y in range(x+1, len(friend_list)):
            friend2 = friend_list[y]
            if A[friend1][friend2] == 1:
                TriCl += 1;
    PossTriCl = len(friend_list)*(len(friend_list)-1)/2  # 间接朋友
    if PossTriCl == 0:
        ClCo = 0
    else:
        ClCo = TriCl / PossTriCl  # 聚集系数
    ClCo_dict[person] = ClCo

最后，我们在控制台里打印出各节点聚集系数的情况。

print()
print('clustering coefficient as following:')
ClCo_list = list(ClCo_dict.items())
ClCo_list.sort(key=lambda x: x[1], reverse=True)
if len(ClCo_dict) < 10:
    for item in ClCo_list:
        print('node', str(item[0]) + ':', '%.2f' % item[1])
else:
    for item in ClCo_list[0:10]:
        print('node', str(item[0]) + ':', '%.2f' % item[1])

控制台输出如下：

请输入邻接矩阵文件名：net3.txt

clustering coefficient as following:
node 1: 1.00
node 3: 1.00
node 0: 0.67
node 2: 0.67

接着计算网络中各边的嵌入性。利用friend_dict遍历所有边、计算两个人的共同朋友数。

embd_dict = {}
for(person, friend_list) in friend_dict.items():
    for friend_a in friend_list:
        if friend_a > person:
            embd_dict[person, friend_a] = 0
            for friend_b in friend_dict[friend_a]:
                if friend_b in friend_list:
                    embd_dict[person, friend_a] += 1

输出结果到控制台。

print()
print('embeddedness as following:')
embd_list = list(embd_dict.items())
embd_list.sort(key=lambda x: x[1], reverse=True)
if len(embd_list) < 10:
    for item in embd_list:
        print('edge', end=' ')
        print(item[0], end='')
        print(':', str(item[1]))
else:
    for item in embd_list[0:10]:
        print('edge', end=' ')
        print(item[0], end='')
        print(':', str(item[1]))

输出结果如下：

请输入邻接矩阵文件名：net3.txt

embeddedness as following:
edge (0, 2): 2
edge (0, 3): 2
edge (2, 3): 2
edge (0, 1): 1
edge (1, 2): 1

2.2、友谊悖论的验证

2.2.1、作业描述与算法思路

本次作业的主要任务是验证友谊悖论。这一悖论说的是，现实中多数人一般都感到朋友的朋友多于自己的朋友；尽管，直观上我们会觉得，既然有人觉得朋友的朋友多于自己的朋友，另一些人就会觉得朋友的朋友少于自己的朋友。

验证这一悖论，要在某个社会网络中进行。为了得到亟待验证的社会网络，一个方法当然是以现实生活的数据为基础、进行抽象和转化，我们在这次作业中采取的是另一个方法：基于“小世界”现象，生成一系列的网络。社会科学以“小世界”为主题的研究颇多，这些成果保证，我们生成的社会网络是对真实世界的合理模拟。

“小世界”现象指的是，邻接矩阵中任意两个点之间，都有一条很短的路径可以通达。之所以“小世界”现象存在，是因为社会网络有如下两个性质：

• 同质性（homophily）：一个圈子里的人往往互相都认识，网络中应当有很多三角形（参见第二讲三元闭包）。我们用==初始规则度数r模拟同质性，表示每一节点和编码相邻的节点之间的边数。这样，编码相近的节点之间会形成很多三角关系。

• 随机性（randomness）：除了小圈子以外，网络中还存在一些跨圈的边，这些边连接的两个节点没有共同朋友（没有形成三元闭包）。这些边的形成不是由于同处一个圈子，或多或少体现了随机性。是这些边保证了任意两点之间有一条很短的路径；否则，要连接不在同一圈子的节点时（例如，要把澳洲的一个庄园主和一个叙利亚难民连接起来），必须借助相邻节点之间的一条条规则边，甚至如此“翻山越岭”也不一定能连接起两个节点。我们用随机调整边占比p来模拟随机性：按照初始规则度数生成的边中，比例为p的边被删除， 同样数量的边随机地在任意两点间生成。

改变初始规则度数r、随机调整边占比p、总节点数n，我们就可以得到一系列不同的社会网络。它们都有“小世界”现象，只是同质性、随机性和规模有所不同。对于每一网络，我们都来检验友谊悖论是否成立。

为了检验某一网络是否存在友谊悖论，我一一检查网络中的每一节点。对于节点i，如果他的朋友数（度数degree）比他朋友的平均度数小不少，那么节点i就存在友谊悖论。如果节点i度数刚好小于邻居的平均度数，节点i很难明显感觉到朋友比自己更受欢迎。我具体设定的悖论觉知门槛是，节点i度数的1.1倍小于邻居的平均度数。对于整个网络，如果超过一半的节点都觉知到了友谊悖论，这一网络就存在友谊悖论。

2.2.2、编程实现与要点说明

提前说明：笔者在写文件做了时间记录，但是我这里有报错，故删了，代码略微变动，不影响结果处理。

首先，我们需要一个生成社会网络的函数neighbor_generator：输入总节点数n、初始规则度数r、随机调整边占比p，这个函数会输出一个表示社会网络的矩阵matr（numpy 2d-array）。

def neighbor_generator(n, r, p):
    file = open('./output/generator_logs_{}', 'w')
    matr = np.zeros((n, n))

初始规则边的建立：每一节点与相邻r个节点建立规则边。当n是偶数时，使节点i与编码∈[i+1, i+|r/2+1+(r mod 2)|]的节点建立边即可；当n是奇数时，执行同样的操作后，还需要删除(n−1)/2条边。这样操作后，总边数为(n×r)/2。

	file.write('Generating an orderly matrix with homophilous links...\n')
    edge_list = []
    for i in range(0, n):
        j_list = [(i + x) % n for x in range(1, int(r/2 + 1 + r % 2))]
        for j in j_list:
            matr[i][j] = 1
            matr[j][i] = 1
            if j > i:
                edge_list.append([i, j])
            else:
                edge_list.append([j, i])
    file.write('Writing the list of node pairs which do not have an edge...\n')
    empt_list = []
    for i in range(0, n):
        if i % 100 == 0:
            file.write('%i nodes processed...' % i)
        for j in range(i+1, n):
            if matr[i][j] == 0:
                empt_list.append([i, j])
    file.write('For now, number of edges in Matrix A: %i\n' % np.sum(matr))
    if r % 2 != 0:
        for i in range(0, n-1, 2):
            matr[i][i+1] = 0
            matr[i+1][i] = 0
            edge_list.remove([i, i+1])
            edge_list.remove([i, i+1])
    file.write('Number of edges in Matrix A: %i\n' % np.sum(matr))

随机调整边：对于已建立的规则边（存储在exc_edge中），比例为p的边被删除，并随机在无关系的两个节点之间（存储在exc_empt中）生成新边。

    file.write('Introducing randomness...\n')
    exc_edge = random.sample(edge_list, int(n * r * p / 2))  # 随机获取n*r*p/2个元素作为一个片断返回
    exc_empt = random.sample(empt_list, int(n * r * p / 2))
    for item in exc_edge:
        matr[item[0]][item[1]] = 0
        matr[item[1]][item[0]] = 0
    for item in exc_empt:
        matr[item[0]][item[1]] = 1
        matr[item[1]][item[0]] = 1

输出矩阵

    np.savetxt('./output/neighbor_original_{}', matr, fmt='%i')
    return matr

除此之外，我们还需要一个验证友谊悖论的函数paradox：输入一个给定的矩阵，输出一个bool值，即它是否满足友谊悖论。

def paradox(matr, n):

我先把“谁是谁的朋友”存储在字典变量fr_dict中，再用这个字典变量计算：节点i的度数，存储在dg_dict[i]['self']；ta邻居的平均度数，存储在dg_dict[i]['nb']。

	fr_dict = {}
    dg_dict = {}
    # generate fr_dict to store who's whose friend
    for i in range(0, n):
        fr_dict[i] = []
        for j in range(0, n):
            if matr[i][j] == 1:
                fr_dict[i].append(j)

    # generate the degrees of individuals
    for i in range(0, n):
        dg_dict[i] = {}
        dg_dict[i]['self'] = len(fr_dict[i])

    # generate the average degrees of neighbors
    for i in range(0, n):
        dg_dict[i]['nb'] = 0
        for friend in fr_dict[i]:
            if fr_dict[i] == []:
                dg_dict[i]['nb'] = 0
            else:
                dg_dict[i]['nb'] += dg_dict[friend]['self'] / len(fr_dict[i])

如果节点i的度数的1.1倍小于邻居的平均度数，ta就存在友谊悖论。如果网络中所有节点超过55%存在友谊悖论（pdScale > 0.55），这一网络就存在友谊悖论。

    pdIndex = 0
    for i in range(0, n):
        if 1.1 * dg_dict[i]['self'] < dg_dict[i]['nb']:
            pdIndex +=1
    pdScale = pdIndex / n
    return [pdScale, pdScale > 0.55]

由于生成矩阵使用了随机数，随机过程的干扰可能导致单次生成的矩阵是一个特殊情况，对验证结论产生很大影响。因此，我们还需要一个计算友谊悖论期望值的函数pdE_calculator：输入一组特定的自变量（总节点数n、初始规则度数r、随机调整边占比p），运行矩阵生成函数一定次数loopCount，计算出现友谊悖论的节点比例pdScale的平均值，我们就得到该网络的友谊悖论期望值pdE。

def pdE_calculator(n, r, p, loopCount = 100):  # paradox expectation
    k = 0
    pdSum = 0
    while True:
        matr = neighbor_generator(n, r, p)
        pdScale = paradox(matr, n)[0]
        k += 1
        pdSum += pdScale
        if k == int(loopCount):
            print('given n = %i, r = %i, p = %.2f, the paradox scale has been successfully calculated' % (n, r, p), end='\n')
            break
        if n >= 500 or loopCount >= 300:
            if k == 1 :
                print('wait a few seconds for the computer to process...', end ='\r')
        if n >= 500 and k % int(5000 / n) == 0 and k > 10:
            print('%i out of %i rounds have been successfully runned........' % (k, loopCount), end='\r')
        if loopCount >= 300 and k % 100 == 0 and k > 300:
            print('%i out of %i rounds have been successfully runned........' % (k, loopCount), end='\r')
    pdE = pdSum / loopCount
    return pdE

除此之外，我还定义了一个输出结果的函数pdOutput，便于反复调用。输入一组自变量值parameterList和对应的友谊悖论验证结果pdEList，它能在控制台打印结果、在csv文件中写入结果、使用matplotlib绘图。

def pdOutput(parameter, parameterList, pdEList, f):
    print('Paradox scales of different %s values as following...' % parameter)
    f.write('%s,' % parameter)
    for i in parameterList:
        print(i, end='/t')
        f.write(str(i)+',')
    print()
    f.write('\nParadox Expectation,')
    for pd in pdEList:
        print('%.3f' % pd, end='\t')
        f.write('%.3f' % pd + ',')
    print()
    f.write('\n')
    xPoints = np.array(parameterList)
    yPoints = np.array(pdEList)
    plotNumDict = {'n': 1, 'r': 2, 'p': 3}
    plt.subplot(2, 2, plotNumDict[parameter])
    plt.plot(xPoints, yPoints, marker='*', color='orange')
    plt.xlabel('%s values' % parameter)
    plt.ylabel('average paradox scales')
    plt.show()

先准备好记录输出的csv文件。

resultDir = './output'
if os.path.isdir(resultDir):
    pass
else:
    os.makedirs(resultDir)
fname = './output/paradox.csv'
f = open(fname, 'w')

我们先来验证，不同的网络规模n对友谊悖论发生期望的影响。给定,r=5,p=0.25，n∈{50,100,150,200,300,500,600,800,1000}。对于每一个n值，我们调用pdMean函数，设定loopCount为100，计算发生友谊悖论的比例，结果存储在n_pdList里。

n_start = time.time()
print('*** Calculating paradox scales given different n values ***')
n_list = [50, 100, 150, 200, 300, 500, 600, 800, 1000]  # more than 7 groups to make the tendency more explicit
n_pdList = []
for n in n_list:
    n_pdE = pdE_calculator(n=n, r=5, p=0.25)
    n_pdList.append(n_pdE)
pdOutput('n', n_list, n_pdList, f)
n_end = time.time()
n_span = n_end - n_start
n_time = '%i min %i s' % (n_span // 60, n_span % 60)
print('Paradox scales calculating of different n values cost', n_time)
print()

输出结果如下：

*** Calculating paradox scales given different n values ***
given n = 50, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 150, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 200, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 300, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 500, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 600, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 800, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 1000, r = 5, p = 0.25, the paradox scale has been successfully calculated
Paradox scales of different n values as following...
50/t100/t150/t200/t300/t500/t600/t800/t1000/t
0.466	0.464	0.466	0.465	0.469	0.470	0.466	0.467	0.466	
Paradox scales calculating of different n values cost 5 min 56 s

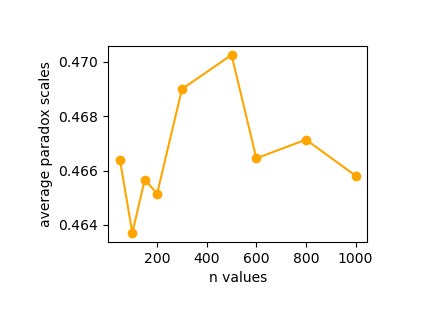
同理，我们再来验证，初始规则度数不同时，友谊悖论发生期望有何不同。给定n=100,p=0.25，r∈{3,4,5,6,7,8,9,10}，设定loopCount为100。

print('*** Calculating paradox scales given different r values ***')
r_list = [3, 4, 5, 6, 7, 8, 9, 10]
r_pdList = []
for r in r_list:
    r_pdE = pdE_calculator(n=100, r=r, p=0.25)
    r_pdList.append(r_pdE)
pdOutput('r', r_list, r_pdList, f)
r_end = time.time()
r_span = r_end - n_end
r_time = '%i min %i s' % (r_span // 60, r_span % 60)
print('Paradox scales calculating of different r values cost', r_time)
print()

输出结果如下：

*** Calculating paradox scales given different r values ***
given n = 100, r = 3, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 4, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 6, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 7, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 8, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 9, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 10, p = 0.25, the paradox scale has been successfully calculated
Paradox scales of different r values as following...
3/t4/t5/t6/t7/t8/t9/t10/t
0.531	0.505	0.468	0.468	0.443	0.428	0.404	0.400	
Paradox scales calculating of different r values cost 0 min 14 s

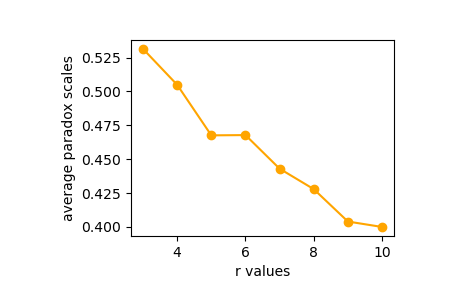
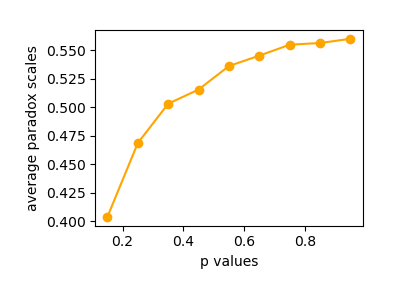
同理，我们最后来验证，随机调整边占比p不同时，友谊悖论发生期望有何不同。给定n=100,r=5,p∈{0.15,0.25,0.35,0.45,0.55,0.65,0.75,0.85,0.95}。

注意到，p越大，随机数对矩阵生成的扰动就越大，我们需要增加循环数，亦即增加矩阵生成次数loopCount，保证友谊悖论节点比例的平均值能达致稳定。因此，我将循环数设为75/(1−p)。

print('*** Calculating paradox scales given different p values ***')
p_list = [0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.85, 0.95]
p_pdList = []
for p in p_list:
    p_loop = 75 / (1 - p)
    p_pdE = pdE_calculator(100, 5, p, p_loop)
    p_pdList.append(p_pdE)
pdOutput('p', p_list, p_pdList, f)
p_end = time.time()
p_span = p_end - r_end
p_time = '%i min %i s' % (p_span // 60, p_span % 60)
print('Paradox scales calculating of different p values cost', p_time)
print()

输出结果如下：

*** Calculating paradox scales given different p values ***
given n = 100, r = 5, p = 0.15, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.25, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.35, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.45, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.55, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.65, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.75, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.85, the paradox scale has been successfully calculated
given n = 100, r = 5, p = 0.95, the paradox scale has been successfully calculated
Paradox scales of different p values as following...
0.15/t0.25/t0.35/t0.45/t0.55/t0.65/t0.75/t0.85/t0.95/t
0.404	0.469	0.503	0.516	0.536	0.545	0.555	0.556	0.560	
Paradox scales calculating of different p values cost 0 min 59 s

2.2.3、结果分析

n	50	100	150	200	300	500	600	800	1000
Paradox Expectation	0.466	0.464	0.466	0.465	0.469	0.470	0.466	0.467	0.466
r	3	4	5	6	7	8	9	10
Paradox Expectation	0.531	0.505	0.468	0.468	0.443	0.428	0.404	0.400
p	0.15	0.25	0.35	0.45	0.55	0.65	0.75	0.85	0.95
Paradox Expectation	0.404	0.469	0.503	0.516	0.536	0.545	0.555	0.556	0.560

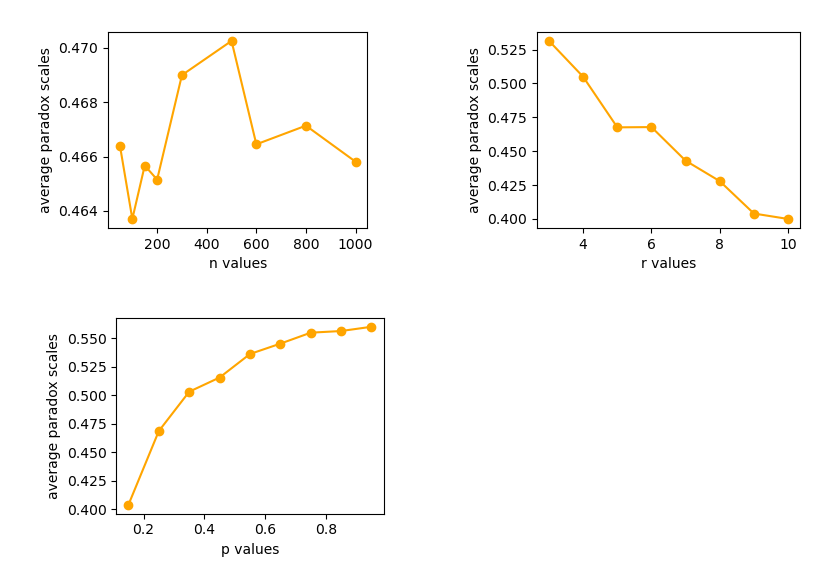
可以得出：

• 社会网络规模n对友谊悖论节点比例平均值的影响不明朗。
• 随着初始规则度数r变大，友谊悖论在全网络中的占比变小，友谊悖论更加弱。当r≥5时，友谊悖论在全网络中的比例低于0.5，不再是一个社会普遍的现象。
• 随着随机调整边占比p变大，友谊悖论在全网络中的占比变大，友谊悖论更加明显。当p≥0.35时，友谊悖论在全网络中的比例高于0.5，可以说这时友谊悖论是一个普遍现象。

进一步的验证，还需要优化模型、增加取值、增加pdE_calculator()循环数loopCount后，进行严谨的统计学分析。我们的初步结论是，当较小、较大时，友谊悖论在全网络中的比例高于0.5，可以说这时友谊悖论是一个普遍现象。

标签：given,嵌入,paradox,list,社会科学,dict,悖论,节点,friend
来源： https://www.cnblogs.com/wangzheming35/p/15861343.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。