标签：02 frac 数学模型 boldsymbol end bmatrix partial 动态 vdots

参考教材：《Modern Control Engineering 5th Edition》Katsuhiko Ogata

第02章 动态系统的数学模型

简单了解状态空间表示（State Space Representation）

教材上p35-39介绍了一个通用的方法，不过因为SSR不是本学期的重点，所以课上没讲，自己所以也暂时没有细看。

通过设置合适的变量，可以将高阶微分方程（组）改写为一阶微分方程组，再以向量的形式表示就得到了该系统的SSR：

\[\left\{ \begin{aligned} \dot{\boldsymbol{x}}(t) &=A \boldsymbol{x}(t)+\boldsymbol{b} u(t) \\ y(t) &=\boldsymbol{c}^{T} \boldsymbol{x}(t)+d u(t) \end{aligned} \right. \]

还可以写向量化更彻底的形式：

\[\begin{bmatrix} \dot{\boldsymbol{x}}\\ y \end{bmatrix} = \begin{bmatrix} A & \boldsymbol{b}\\ \boldsymbol{c}^T & d \end{bmatrix} \begin{bmatrix} \boldsymbol{x}\\ u \end{bmatrix} \]

特点

• 一阶常系数线性微分方程组
• \(A\)是一个方阵
• 其它暂时不了解

非线性系统的线性化

非线性系统

\[\left\{ \begin{aligned} \dot{\boldsymbol x}&=\boldsymbol f(\boldsymbol x, u)\\ y&=g(\boldsymbol x, u) \end{aligned} \right. \]

• 平衡点

  当输入\(u(t)=u_0\)时，\(\dot{\boldsymbol x}=\boldsymbol f(\boldsymbol x_0, u_0)\)，此时的\(\boldsymbol x\)处于平衡态。

• 向量导数的定义

  \[\frac{\partial g}{\partial \boldsymbol x^T}\triangleq \begin{bmatrix} \frac{\partial g}{\partial x_1} & \frac{\partial g}{\partial x_2}&\dots&\frac{\partial g}{\partial x_n} \end{bmatrix}\\ \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}^{T}} \triangleq\left[\begin{array}{c} \frac{\partial f_{1}}{\partial \boldsymbol{x}^{T}} \\ \frac{\partial f_{2}}{\partial \boldsymbol{x}^{T}} \\ \vdots \\ \frac{\partial f_{n}}{\partial \boldsymbol{x}^{T}} \end{array}\right]=\left[\begin{array}{cccc} \frac{\partial f_{1}}{\partial x_{1}} & \frac{\partial f_{1}}{\partial x_{2}} & \ldots & \frac{\partial f_{1}}{\partial x_{n}} \\ \frac{\partial f_{2}}{\partial x_{1}} & \frac{\partial f_{2}}{\partial x_{2}} & \ldots & \frac{\partial f_{2}}{\partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{n}}{\partial x_{1}} & \frac{\partial f_{n}}{\partial x_{2}} & \ldots & \frac{\partial f_{n}}{\partial x_{n}} \end{array}\right] \]

• 线性化

  • 思想：在平衡点附近，用一阶近似代替非线性函数

  • 计算

    令\(\dot{\boldsymbol x}_\delta=\dot{\boldsymbol x}-\dot{\boldsymbol x}_0\)，\(u_\delta=u-u_0\)，则

    \[\begin{bmatrix} \dot{\boldsymbol{x}}_\delta\\ y_\delta \end{bmatrix} = \begin{bmatrix} A & \boldsymbol{b}\\ \boldsymbol{c}^T & d \end{bmatrix} \begin{bmatrix} \boldsymbol{x}_\delta\\ u_\delta \end{bmatrix} \]

    其中

    \[\begin{bmatrix} A & \boldsymbol{b}\\ \boldsymbol{c}^T & d \end{bmatrix} = \begin{bmatrix} \left.\frac{\partial \boldsymbol f}{\partial\boldsymbol{x}^{T}}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0} & \left.\frac{\partial \boldsymbol f}{\partial u}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0}\\ \left.\frac{\partial g}{\partial \boldsymbol{x}^{T}}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0} & \left.\frac{\partial g}{\partial u}\right|_{\boldsymbol x=\boldsymbol x_0\atop u=u_0} \end{bmatrix} \]

三种表示法的相互转换

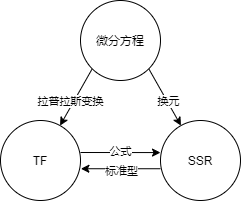
从微分方程到TF

• 回忆信号与系统，要注意前提是假设所有的初态都是0。
• 系统的单位冲激响应的拉普拉斯变换即是系统的TF。

从微分方程到SSR

见“简单了解状态空间表示”。

从SSR到TF（单入单出系统）

对SSR进行拉普拉斯变换得到

\[\left\{ \begin{aligned} s\tilde{\boldsymbol{x}}(x) &=A\tilde{\boldsymbol{x}}(s)+\boldsymbol{b} \tilde u(s) \\ \tilde y(s) &=\boldsymbol{c}^{T} \tilde{\boldsymbol{x}}(s)+d \tilde u(s) \end{aligned} \right. \]

消去\(\tilde{\boldsymbol x}(s)\)得到

\[\tilde y(s)=[\boldsymbol c^T(sI-A)^{-1}\boldsymbol b+d]\tilde u(s) \]

由系统的单位冲激响应的拉普拉斯变换即是系统的传递函数，得

\[G(s)=\boldsymbol c^T(sI-A)^{-1}\boldsymbol b+d=\frac{\boldsymbol c^T\mathrm{adj}(sI-A)^{-1}\boldsymbol b}{\mathrm{det}(sI-A)}+d \]

从TF到SSR（只记录了结论）

能控和能观标准型

n阶微分方程对应的TF待定系数最多有\(2n+2\)，而对应的SSR的待定系数有\(n^2+2n+1\)个，所以从TF到SSR不唯一，故定义了一些标准型。假设有TF如下：

\[G(s)=\frac{b_ns^n+{b}_{n-1} s^{n-1}+{b}_{n-2} s^{n-2}+\cdots+{b}_{1} s+{b}_{0}}{s^{n}+a_{n-1} s^{n-1}+\cdots+a_{1} s+a_{0}}=\frac{\hat{b}_{n-1} s^{n-1}+\hat{b}_{n-2} s^{n-2}+\cdots+\hat{b}_{1} s+\hat{b}_{0}}{s^{n}+a_{n-1} s^{n-1}+\cdots+a_{1} s+a_{0}}+b_{n} \]

其中\(\hat b_i=b_i-b_na_i\)。则对应的SSR矩阵如下：

	\(A\)	\(\boldsymbol b\)	\(\boldsymbol c\)	\(d\)
能控标准型	\(\begin{bmatrix}0 & 1 & 0 & \cdots & 0\\0 & 0 & 1 & \cdots & 0\\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \cdots & 1\\-a_0 & -a_1 & -a_2 &\cdots & -a_{n-1}\end{bmatrix}\)	\(\begin{bmatrix}0\\0\\\vdots\\0\\1\end{bmatrix}\)	\(\begin{bmatrix}\hat b_0\\\hat b_1\\\vdots\\\hat b_{n-2}\\\hat b_{n-1}\end{bmatrix}\)	\(b_n\)
能观标准型	\(\begin{bmatrix}0 & 0 & \cdots & 0 & -a_0\\1 & 0 & \cdots & 0 & -a_1\\0 & 1 & \cdots & 0 & -a_2\\\vdots & \vdots & \ddots & \vdots & \vdots \\0 & 0 & \cdots &1 & -a_{n-1}\end{bmatrix}\)	\(\begin{bmatrix}\hat b_0\\\hat b_1\\\vdots\\\hat b_{n-2}\\\hat b_{n-1}\end{bmatrix}\)	\(\begin{bmatrix}0\\0\\\vdots\\0\\1\end{bmatrix}\)	\(b_n\)

对角和约当标准型

对角标准型

如果有n个不同的极点，TF可改写为：

\[G(s)=b_n+\frac{c_1}{s-p_1}+\frac{c_2}{s-p_2}+\dots+\frac{c_n}{s-p_n} \]

其中\(c_i\)可由留数定理确定：\(c_i=\lim_\limits{s\to p_i}(s-p_i)G(s)\)。则SSR表示为

\[A =\begin{bmatrix}p_1 & 0 & \cdots & 0\\0 & p_2 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots\\0 & 0 & \cdots & p_n\end{bmatrix},\quad\boldsymbol b=\begin{bmatrix}1\\1\\\vdots\\1\end{bmatrix},\quad\boldsymbol c=\begin{bmatrix}c_1\\c_2\\\vdots\\c_n\end{bmatrix},\quad d=b_n \]

约当标准型

如果有重极点，TF可改写为：

\[\begin{aligned} G(s)=& \frac{c_{1,1}}{\left(s-p_{1}\right)^{n_{1}}}+\frac{c_{1,2}}{\left(s-p_{1}\right)^{n_{1}-1}}+\cdots+\frac{c_{1, n_{1}}}{s-p_{1}} \\ &+\frac{c_{2,1}}{\left(s-p_{2}\right)^{n_{2}}}+\frac{c_{2,2}}{\left(s-p_{2}\right)^{n_{2}-1}}+\cdots+\frac{c_{2, n_{2}}}{s-p_{2}}+\cdots \\ &+\frac{c_{m, 1}}{\left(s-p_{m}\right)^{n_{m}}}+\frac{c_{m, 2}}{\left(s-p_{m}\right)^{n_{m}-1}}+\cdots+\frac{c_{m, n_{m}}}{s-p_{m}}+b_{n} \end{aligned} \]

其中\(c_{i,j}\)可由留数定理确定：\(c_{i,j}=\frac{1}{(j-1)!}\lim_\limits{s\to p_i}\frac{\mathrm{d}^{j-1}}{\mathrm{d}s^{j-1}}(s-p_i)^jG(s)\)。则SSR表示为

\[A =\begin{bmatrix}J_1 & 0 & \cdots & 0\\0 & J_2 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots\\0 & 0 & \cdots & J_m\end{bmatrix},\quad\boldsymbol b=\begin{bmatrix}\boldsymbol b_1\\\boldsymbol b_2\\\vdots\\\boldsymbol b_m\end{bmatrix},\quad\boldsymbol c=\begin{bmatrix}\boldsymbol c_1\\\boldsymbol c_2\\\vdots\\\boldsymbol c_m\end{bmatrix},\quad d=b_n \]

其中

\[J_i= \begin{bmatrix} p_i & 1 & 0 & \cdots & 0 & 0\\ 0 & p_i & 1 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & \cdots & 1 & 0\\ 0 & 0 & 0 & \cdots & p_i & 1\\ 0 & 0 & 0 & \cdots & 0 & p_i \end{bmatrix} ,\quad \boldsymbol b_i= \begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 1 \end{bmatrix} ,\quad \boldsymbol c_i= \begin{bmatrix} c_{i,1}\\c_{i,2}\\\vdots\\c_{i,n_i} \end{bmatrix} \]

常见物理模型及其建模

电路	力学
电阻\(v(t)=Ri(t)\)	阻尼\(v(t)=\frac{1}{b}f(t)\)
电感\(v(t)=L\frac{{\rm d}i(t)}{{\rm d}t}\)	弹簧\(v(t)=\frac{1}{k}\frac{{\rm d}f(t)}{{\rm d}t}\)
电容\(i(t)=C\frac{{\rm d}v(t)}{{\rm d}t}\)	质量\(f(t)=m\frac{{\rm d}v(t)}{{\rm d}t}\)

框图和信号流图

• 框图化简

  • 并联：\(\boldsymbol G=\boldsymbol G_1+\boldsymbol G_2\)

  • 串联：\(\boldsymbol G=\boldsymbol G_2\boldsymbol G_1\)（\(G_2\)连在\(G_1\)之后）

  • 反馈：\(\boldsymbol G_c=\frac{\boldsymbol G}{1+\boldsymbol G\boldsymbol H}\)（负反馈为+，正反馈则要改成-）

  • 移动求和点：\(\tilde{\boldsymbol{y}}=\boldsymbol{G} \tilde{\boldsymbol{r}}+\tilde{\boldsymbol{d}}=\boldsymbol{G}\left(\tilde{\boldsymbol{r}}+\boldsymbol{G}^{-1} \tilde{\boldsymbol{d}}\right)\)

    

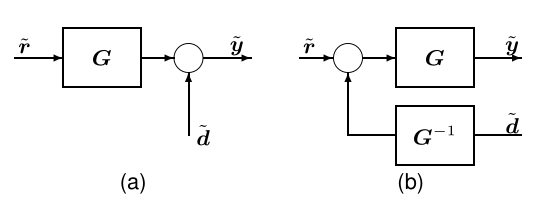
  • 移动分支点：添加\(\boldsymbol G\)或者\(\boldsymbol G^{-1}\)

• 信号流图的梅森公式：一种通过流程化的将信号流图转换为TF的方法，计算相对麻烦。

  

  • 注意“removed“是节点也要去一起去掉。

标签：02,frac,数学模型,boldsymbol,end,bmatrix,partial,动态,vdots
来源： https://www.cnblogs.com/harold-lu/p/15390612.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。