标签:cos 三角函数 dfrac 初步 beta alpha tan sin
一,定义
1.1 锐角三角函数
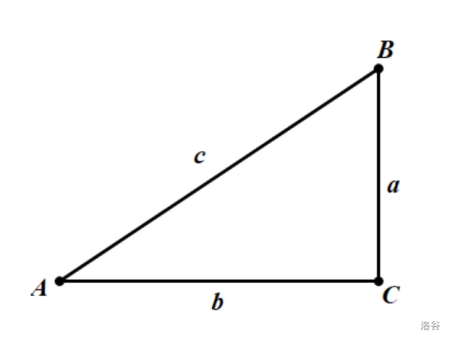
如图,在 \({\rm Rt}\triangle ABC\) 中,\(\angle C=90^{\circ}\) ,则有:
-
\(\sin A=\dfrac ac\) (正弦值等于对边比斜边)
-
\(\cos A=\dfrac bc\) (余弦值等于邻边比斜边)
-
\(\tan A=\dfrac ab\) (正切值等于对边比邻边)
-
\(\cot A=\dfrac ba\) (余切值等于邻边比对边)
-
\(\sec A=\dfrac cb\) (正割值等于斜边比邻边)
-
\(\csc A=\dfrac ca\) (余割值等于斜边比对边)
中学阶段最常用的是 \(\sin,\cos,\tan,\cot\)
下文将不再讨论 \(\sec,\csc\) 及其他三角函数
1.2 任意角三角函数
构造平面直角坐标系 \(xOy\)
将 \(x\) 轴正半轴绕点 \(O\) 逆时针旋转一个角度 \(\theta\) 得到射线 \(l\)
设 \(P(x,y)\) 为 \(l\) 上一点,\(OP=r\) ,则有:
-
\(\sin\theta=\dfrac yr\)
-
\(\cos\theta=\dfrac xr\)
-
\(\tan\theta=\dfrac yx\)
-
\(\cot\theta=\dfrac xy\)
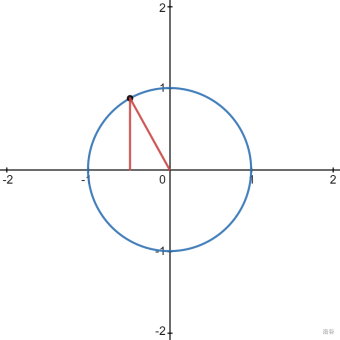
下图是 \(\alpha\in(\frac{\pi}2,\pi)\) 的情况
黑点为 \(l\) 与单位圆的交点,其横坐标即为 \(\cos\alpha\) ,纵坐标即为 \(\sin\alpha\)
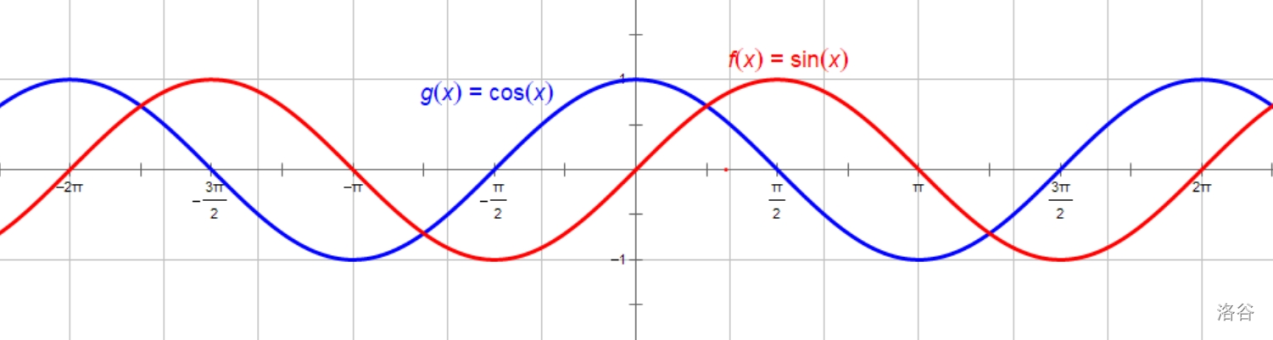
\(\sin\) 和 \(\cos\) 的函数图象如下图所示
1.3 反三角函数
反三角函数指三角函数的反函数,用 arc + 函数名 的形式表示
如 \(\arctan\dfrac ab\) 表示满足 \(\tan\theta=\dfrac ab\) 的 \(\theta\) 值
\(\arctan\) 的值域(主值区间)为 \((-\frac\pi 2,\frac\pi 2)\) ,这是为了保证一个自变量恰好对应一个函数值,同时方便使用
\(\arcsin,\arccos,\operatorname{arccot}\) 的值域可参考 2.1 中表格
二,基本性质
2.1 定义域 & 值域
| 三角函数 | 定义域 | 值域 | 反三角函数 | 定义域 | 值域(主值区间) |
|---|---|---|---|---|---|
| \(\sin\) | \(\mathbb R\) | \([-1,1]\) | \(\arcsin\) | \([-1,1]\) | \([-\frac\pi 2,\frac\pi 2]\) |
| \(\cos\) | \(\mathbb R\) | \([-1,1]\) | \(\arccos\) | \([-1,1]\) | \([0,\pi]\) |
| \(\tan\) | \(\{x\mid x\ne k\pi+\frac\pi 2(k\in \mathbb Z)\}\) | \(\mathbb R\) | \(\arctan\) | \(\mathbb R\) | \((-\frac\pi 2,\frac\pi 2)\) |
| \(\cot\) | \(\{x\mid x\ne k\pi(k\in \mathbb Z)\}\) | \(\mathbb R\) | \(\operatorname{arccot}\) | \(\mathbb R\) | \((0,\pi)\) |
2.2 奇偶性 & 单调性 & 周期性
| 三角函数 | 奇偶性 | 最小正周期 | 反三角函数 | 奇偶性 | 单调性 |
|---|---|---|---|---|---|
| \(\sin\) | 奇 | \(2\pi\) | \(\arcsin\) | 奇 | 单调递增 |
| \(\cos\) | 偶 | \(2\pi\) | \(\arccos\) | 非奇非偶 | 单调递减 |
| \(\tan\) | 奇 | \(\pi\) | \(\arctan\) | 奇 | 单调递增 |
| \(\cot\) | 奇 | \(\pi\) | \(\operatorname{arccot}\) | 非奇非偶 | 单调递减 |
\(\sin,\cos,\tan,\cot\) 的单调性请自行画图判断
\(\arcsin,\arccos,\arctan,\operatorname{arccot}\) 都不是周期函数
2.3 对称性
2.4 特殊值
| \(\theta\rm(deg)\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\theta\rm(rad)\) | \(0\) | \(\dfrac\pi6\) | \(\dfrac\pi4\) | \(\dfrac\pi3\) | \(\dfrac\pi2\) | \(\dfrac{2\pi}3\) | \(\dfrac{3\pi}4\) | \(\dfrac{5\pi}6\) | \(\pi\) |
| \(\sin\theta\) | \(0\) | \(\dfrac12\) | \(\dfrac{\sqrt2}2\) | \(\dfrac{\sqrt3}2\) | \(1\) | \(\dfrac{\sqrt3}2\) | \(\dfrac{\sqrt2}2\) | \(\dfrac12\) | \(0\) |
| \(\cos\theta\) | \(1\) | \(\dfrac{\sqrt3}2\) | \(\dfrac{\sqrt2}2\) | \(\dfrac12\) | \(0\) | \(-\dfrac12\) | \(-\dfrac{\sqrt2}2\) | \(-\dfrac{\sqrt3}2\) | \(-1\) |
| \(\tan\theta\) | \(0\) | \(\dfrac{\sqrt3}3\) | \(1\) | \(\sqrt3\) | \(\backslash\) | \(-\sqrt3\) | \(-1\) | \(-\dfrac{\sqrt3}3\) | \(0\) |
| \(\cot\theta\) | \(\backslash\) | \(\sqrt3\) | \(1\) | \(\dfrac{\sqrt3}3\) | \(0\) | \(-\dfrac{\sqrt3}3\) | \(-1\) | \(-\sqrt3\) | \(\backslash\) |
\(15^{\circ}\) 和 \(75^{\circ}\) 的三角函数值也有可能会用到:
\(\sin15^{\circ}=\dfrac{\sqrt6-\sqrt2}4,~~\cos15^{\circ}=\dfrac{\sqrt6+\sqrt2}4,~~\tan15^{\circ}=2-\sqrt3,~~\cot15^{\circ}=2+\sqrt3\)
\(\sin75^{\circ}=\dfrac{\sqrt6+\sqrt2}4,~~\cos75^{\circ}=\dfrac{\sqrt6-\sqrt2}4,~~\tan75^{\circ}=2+\sqrt3,~~\cot75^{\circ}=2-\sqrt3\)
2.5 基本关系式
-
\(\sin^2\theta+\cos^2\theta=1\)
-
\(\tan\theta=\dfrac{\sin\theta}{\cos\theta},~~\cot\theta=\dfrac{\cos\theta}{\sin\theta}\)
-
\(\tan\theta\cot\theta=1\)
-
\(\sin\theta=\cos(90^{\circ}-\theta),~~\tan\theta=\cot(90^{\circ}-\theta)\)
证明略
三,三角恒等变形
3.1 诱导公式
诱导公式的作用是将 \(n\cdot\dfrac\pi2\pm \alpha\) 这种角的三角函数转化为 \(\alpha\) 的三角函数
首先,根据三角函数的周期性,对于 \(\theta=2k\pi+\alpha(k\in\mathbb Z)\) ,有
\(\begin{aligned} \sin(2k\pi+\alpha)&=\sin\alpha\\ \cos(2k\pi+\alpha)&=\cos\alpha\\ \tan(2k\pi+\alpha)&=\tan\alpha\\ \cot(2k\pi+\alpha)&=\cot\alpha \end{aligned}\)
诱导公式的其它部分如下表所示
| \(\theta\rm(deg)\) | \(-\alpha\) | \(90^{\circ}-\alpha\) | \(90^{\circ}+\alpha\) | \(180^{\circ}-\alpha\) | \(180^{\circ}+\alpha\) | \(270^{\circ}-\alpha\) | \(270^{\circ}+\alpha\) | \(360^{\circ}-\alpha\) |
|---|---|---|---|---|---|---|---|---|
| \(\theta\rm(rad)\) | \(-\alpha\) | \(\dfrac\pi2-\alpha\) | \(\dfrac\pi2+\alpha\) | \(\pi-\alpha\) | \(\pi+\alpha\) | \(\dfrac{3\pi}2-\alpha\) | \(\dfrac{3\pi}2+\alpha\) | \(2\pi-\alpha\) |
| \(\sin\theta\) | \(-\sin\alpha\) | \(\cos\alpha\) | \(\cos\alpha\) | \(\sin\alpha\) | \(-\sin\alpha\) | \(-\cos\alpha\) | \(-\cos\alpha\) | \(-\sin\alpha\) |
| \(\cos\theta\) | \(\cos\alpha\) | \(\sin\alpha\) | \(-\sin\alpha\) | \(-\cos\alpha\) | \(-\cos\alpha\) | \(-\sin\alpha\) | \(\sin\alpha\) | \(\cos\alpha\) |
| \(\tan\theta\) | \(-\tan\alpha\) | \(\cot\alpha\) | \(-\cot\alpha\) | \(-\tan\alpha\) | \(\tan\alpha\) | \(\cot\alpha\) | \(-\cot\alpha\) | \(-\tan\alpha\) |
| \(\cot\theta\) | \(-\cot\alpha\) | \(\tan\alpha\) | \(-\tan\alpha\) | \(-\cot\alpha\) | \(\cot\alpha\) | \(\tan\alpha\) | \(-\tan\alpha\) | \(-\cot\alpha\) |
证明全部都可以直接套定义得到,但还是建议结合函数图象的性质理解记忆
3.2 和差角公式
\(\begin{aligned} \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ \sin(\alpha-\beta)&=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\ \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ \cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\ \tan(\alpha+\beta)&=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\ \tan(\alpha-\beta)&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{aligned}\)
证明思路:
前四个中只需任意证明一个,再结合诱导公式即可得出另外三个
然后一三式、二四式分别相除即可得到五、六式
例如 \(\tan(\alpha+\beta)=\dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\dfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\)
分子分母同时约去 \(\cos\alpha\cos\beta\) 即可得到 \(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)
下面给出两种证明方法(在三角形内证明一式、向量法证明四式)
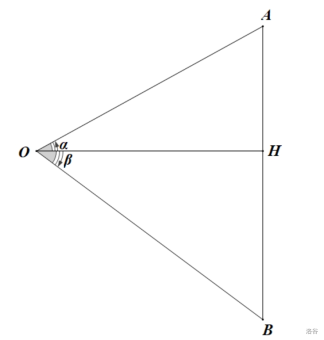
以 \(\alpha,\beta\) 均为锐角的情形为例
\(S_{\triangle AOH}=\dfrac12OA\cdot OH\cdot \sin\alpha=\dfrac12OA\cdot OB\cdot\cos\beta\cdot\sin\alpha\)
\(S_{\triangle BOH}=\dfrac12OB\cdot OH\cdot \sin\beta=\dfrac12OB\cdot OA\cdot\cos\alpha\cdot\cos\beta\)
\(S_{\triangle AOB}=\dfrac12OA\cdot OB\cdot \sin(\alpha+\beta)\)
显然 \(S_{\triangle AOB}=S_{\triangle AOH}+S_{\triangle BOH}\) ,故 \(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\) ,即为一式
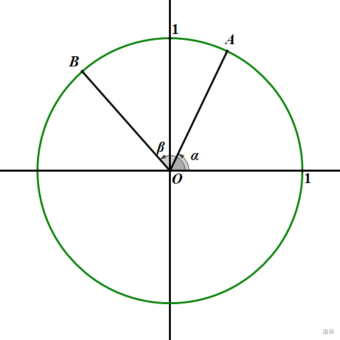
\(A,B\) 都在单位圆上,故 \(A,B\) 的坐标分别为 \((\cos\alpha,\sin\alpha),(\cos\beta,\sin\beta)\)
考虑向量 \(\overrightarrow{OA},\overrightarrow{OB}\) 的数量积
根据定义, \(\overrightarrow{OA}\cdot\overrightarrow{OB}=|OA|\cdot|OB|\cdot\cos(\beta-\alpha)=\cos(\beta-\alpha)=\cos(\alpha-\beta)\)
再考虑数量积的坐标表示,有 \(\overrightarrow{OA}\cdot\overrightarrow{OB}=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
故 \(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\) ,即为四式
3.3 倍角公式
在和角公式中令 \(\alpha=\beta\) ,即可得到二倍角公式:
\(\begin{aligned} \sin2\alpha&=2\sin\alpha\cos\alpha\\ \cos2\alpha&=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha\\ \tan2\alpha&=\dfrac{2\tan\alpha}{1-\tan^2\alpha} \end{aligned}\)
由二倍角公式可得 \(\cos\alpha=2\cos^2\dfrac\alpha2-1=1-2\sin^2\dfrac\alpha2\)
进一步可以推出半角公式:
\(\begin{aligned} \sin\dfrac\alpha2&=\pm\sqrt{\dfrac{1-\cos\alpha}2}\\ \cos\dfrac\alpha2&=\pm\sqrt{\dfrac{1+\cos\alpha}2}\\ \tan\dfrac\alpha2&=\pm\sqrt{\dfrac{1-\cos\alpha}{1+\cos\alpha}}=\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha} \end{aligned}\)
带 \(\pm\) 是因为开方导致符号不确定,还需要根据 \(\dfrac\alpha2\) 所在的象限判断
但 \(\tan\dfrac\alpha2=\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha}\) 是没有符号问题的 可以直接用
三倍角公式偶尔也会用到 但部分推导过程要用到和差化积/积化和差公式 所以放到后面再讲
四倍及以上就没必要记了
3.4 万能公式
功能是仅用 \(\tan\dfrac\alpha2\) 表示出 \(\alpha\) 的三角函数值
首先根据二倍角公式有
\(\begin{aligned} \sin\alpha&=2\sin\dfrac\alpha2\cos\dfrac\alpha2\\ \cos\alpha&=\cos^2\dfrac\alpha2-\sin^2\dfrac\alpha2\\ \tan\alpha&=\dfrac{2\tan\frac\alpha2}{1-\tan^2\frac\alpha2} \end{aligned}\)
三式已经达成目标了
因为 \(1=\sin^2\frac\alpha2+\cos^2\frac\alpha2\) ,所以我们可以把一二式写成
\(\begin{aligned} \sin\alpha&=\dfrac{2\sin\frac\alpha2\cos\frac\alpha2}{\sin^2\frac\alpha2+\cos^2\frac\alpha2}\\ \cos\alpha&=\dfrac{\cos^2\frac\alpha2-\sin^2\frac\alpha2}{\sin^2\frac\alpha2+\cos^2\frac\alpha2} \end{aligned}\)
然后就可以约分了,最终得到
\(\begin{aligned} \sin\alpha&=\dfrac{2\tan\frac\alpha2}{1+\tan^2\frac\alpha2}\\ \cos\alpha&=\dfrac{1-\tan^2\frac\alpha2}{1+\tan^2\frac\alpha2}\\ \tan\alpha&=\dfrac{2\tan\frac\alpha2}{1-\tan^2\frac\alpha2} \end{aligned}\)
即为万能公式
3.6 积化和差公式
根据和差角公式,\(\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\)
两式相加,两式相减,分别可得出
\(\begin{aligned} \cos\alpha\cos\beta&=\dfrac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)]\\ \sin\alpha\sin\beta&=\dfrac12[\cos(\alpha-\beta)-\cos(\alpha+\beta)] \end{aligned}\)
同理,由 \(\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\) 可得
\(\begin{aligned} \sin\alpha\cos\beta&=\dfrac12[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\ \cos\alpha\sin\beta&=\dfrac12[\sin(\alpha+\beta)-\sin(\alpha+\beta)] \end{aligned}\)
这四个式子就是积化和差公式
\(\begin{aligned} \sin\alpha\sin\beta&=-\dfrac12[\cos(\alpha+\beta)-\cos(\alpha-\beta)]\\ \sin\alpha\cos\beta&=\dfrac12[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\ \cos\alpha\sin\beta&=\dfrac12[\sin(\alpha+\beta)-\sin(\alpha+\beta)]\\ \cos\alpha\cos\beta&=\dfrac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)] \end{aligned}\)
3.8 和差化积公式
\(\begin{aligned} \sin\alpha+\sin\beta&=2\sin\tfrac{\alpha+\beta}2\cos\tfrac{\alpha-\beta}2\\ \sin\alpha-\sin\beta&=2\cos\tfrac{\alpha+\beta}2\sin\tfrac{\alpha-\beta}2\\ \cos\alpha+\cos\beta&=2\cos\tfrac{\alpha+\beta}2\cos\tfrac{\alpha-\beta}2\\ \cos\alpha-\cos\beta&=2\cos\tfrac{\alpha+\beta}2\sin\tfrac{\alpha-\beta}2 \end{aligned}\)
证明不写了,用积化和差从右往左推就行
3.9 其它公式
三倍角公式
对二倍角和一倍角用一次和角公式即可
化简整理会用到和差化积/积化和差 不详细写了
\(\begin{aligned} \sin3\alpha&=3\sin\alpha-4\sin^3\alpha=4\sin(60^{\circ}-\alpha)\sin\alpha\sin(60^{\circ}+\alpha) \\ \cos3\alpha&=4\cos^3\alpha-3\cos\alpha=4\cos(60^{\circ}-\alpha)\cos\alpha\cos(60^{\circ}+\alpha) \\ \tan3\alpha&=\dfrac{\tan^3\alpha-3\tan\alpha}{3\tan^2\alpha-1}=\tan(60^{\circ}-\alpha)\tan\alpha\tan(60^{\circ}+\alpha) \end{aligned}\)
辅助角公式
\(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\arctan\frac ba)\)
用和角公式把右边拆了就能证
可以用来处理最值问题
标签:cos,三角函数,dfrac,初步,beta,alpha,tan,sin 来源: https://www.cnblogs.com/REKonib/p/15008291.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。