标签:iy right sumy sumx 题解 texttt chorus 合唱团 left
本文将同步发布于:
题目
题意简述
给定 \(n\),有 \(2n\) 个人排成两排,每个人有一个 \(\texttt{lvl}\) 值,第一排为 \(x_i\),第二排为 \(y_i\)。
现在要求你给第一排的人与第二排的人配对,如果第一排种 \(i\) 与 第二排的 \(j\) 配对,那么第一排中的 \([1,i-1]\) 就不能与 第二排中的 \([j+1,n]\) 配对了(不能交叉)。
如果 \(i,j\) 配对,收益为 \(x_iy_j\);对于每个没有配对的连续段,损失为这个连续段内所有人的 \(\texttt{lvl}\) 值的和的平方。
请你求出收益的最大值。
\(1\leq n\leq 10^3\),\(0\leq\texttt{lvl}_i\leq 10^3\)。
题解
寻找配对的性质
配对不能交叉,所以我们可以想到配对一定会把没有配对的分成一段一段的,并且每一段中没有任何匹配。
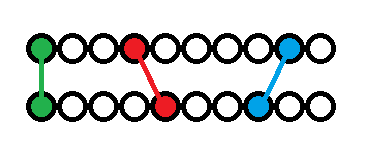
考虑到 \(\texttt{lvl}\geq 0\) 和 \(f(x)=x^2\) 在 \(a,b\geq 0\) 时满足 \(f(a+b)\geq f(a)+f(b)\) 两个性质,我们不难发现,增加一组匹配,答案一定不会变劣。
因此最优解中,一定存在一种情况满足两个相邻的匹配之间,不可能既有 \(x\) 点,又有 \(y\) 点(可以形成新的匹配)。
动态规划
设 \(\texttt{sumx}_i=\sum\limits_{j=1}^ix_j\),\(\texttt{sumy}_i=\sum\limits_{j=1}^iy_j\)。
设 \(f_{i,j}\) 表示,第一排处理到 \(i\),第二排处理到 \(j\),且 \(i,j\) 匹配的最大收益。为了方便,我们直接在两排后面添加两个 \(0\),这样答案为 \(f_{n+1,n+1}\)。
那么我们考虑上一个匹配一定是 \((i-1,k)\) 或者 \((k,j-1)\),轻松列出转移方程。
\[f_{i,j}=x_iy_j+\max\left\{\max_{k=1}^{j-1}\left\{f_{i-1,k}-(\texttt{sumy}_{j-1}-\texttt{sumy}_{k+1})^2\right\},\max_{k=1}^{i-1}\left\{f_{k,j-1}-(\texttt{sumx}_{i-1}-\texttt{sumx}_{k+1})^2\right\}\right\} \]直接动态规划的复杂度为 \(\Theta(n^3)\)。
斜率优化
直接做复杂度不对,我们又无法优化状态设计,就只能思考优化动态规划了。
我们分类讨论,先思考上一个匹配是 \((i-1,k)\) 的情况。
\[f_{i,j}=x_iy_j+\max_{k=1}^{j-1}\left\{f_{i-1,k}-(\texttt{sumy}_{j-1}-\texttt{sumy}_{k+1})^2\right\} \]发现式子中与 \(i\) 有关的值只有 \(i\) 和 \(i-1\),我们考虑暂时视 \(i\) 为定值。
\[f_{i,j}=x_iy_j+\max_{k=1}^{j-1}\left\{f_{i-1,k}-(\texttt{sumy}_{j-1}-\texttt{sumy}_{k+1})^2\right\} \]暂时忽略 \(\max\)。
\[f_{i,j}=x_iy_j+f_{i-1,k}-(\texttt{sumy}_{j-1}-\texttt{sumy}_{k+1})^2 \]展开平方项
\[f_{i,j}=x_iy_j+f_{i-1,k}-\texttt{sumy}_{j-1}^2+2\texttt{sumy}_{j-1}\texttt{sumy}_{k+1}-\texttt{sumy}_{k+1}^2 \]观察到与 \(j\) 相关的项,与 \(k\) 相关的项,与 \(j,k\) 相关的项,不妨尝试斜率优化,整理。
\[\left(\texttt{sumy}_{k+1}^2-f_{i-1,k}\right)=\left(\texttt{sumy}_{j-1}\right)\left(2\texttt{sumy}_{k+1}\right)+\left(x_iy_j-\texttt{sumy}_{j-1}^2-f_{i,j}\right) \]设
\[\begin{cases} y=\texttt{sumy}_{k+1}^2-f_{i-1,k}\\ k=\texttt{sumy}_{j-1}\\ x=2\texttt{sumy}_{k+1}\\ b=x_iy_j-\texttt{sumy}_{j-1}^2-f_{i,j} \end{cases} \]我们发现,我们要求的就是 \(b\) 的最小值,斜率优化维护下凸包即可。
注意到 \(k,x\) 均随 \(j,k\) 单调不降,因此可以用单调队列维护下凸包。
我们同理处理出 \((k,j-1)\) 的情况的式子。
\[\left(\texttt{sumx}_{k+1}^2-f_{k,j-1}\right)=\left(\texttt{sumx}_{i-1}\right)\left(2\texttt{sumx}_{k+1}\right)+\left(x_iy_j-\texttt{sumx}_{i-1}^2-f_{i,j}\right) \]\[\begin{cases} y=\texttt{sumx}_{k+1}^2-f_{k,j-1}\\ k=\texttt{sumx}_{i-1}\\ x=2\texttt{sumx}_{k+1}\\ b=x_iy_j-\texttt{sumx}_{i-1}^2-f_{i,j} \end{cases} \]我们只需要维护 \(2n\)(也可以是 \(n+1\))个凸包即可优化时间复杂度为 \(\Theta(n^2)\)。
参考程序
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
static char buf[1<<21],*p1=buf,*p2=buf;
inline int read(void){
reg char ch=getchar();
reg int res=0;
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) res=10*res+(ch^'0'),ch=getchar();
return res;
}
inline ll max(reg ll a,reg ll b){
return a>b?a:b;
}
const int MAXN=1e3+5;
const ll inf=1e18;
const double eps=1e-6;
inline int sgn(reg double x){
if(fabs(x)<eps)
return 0;
else
return x<0?-1:1;
}
struct Vector{
ll x,y;
inline Vector(reg ll x=0,reg ll y=0):x(x),y(y){
return;
}
inline Vector operator+(const Vector& a)const{
return Vector(x+a.x,y+a.y);
}
inline Vector operator-(const Vector& a)const{
return Vector(x-a.x,y-a.y);
}
};
inline double cross(const Vector& a,const Vector& b){
return 1.0*a.x*b.y-1.0*a.y*b.x;
}
typedef Vector Point;
int n;
int x[MAXN],y[MAXN];
int sumx[MAXN],sumy[MAXN];
ll f[MAXN][MAXN];
int headr[MAXN],tailr[MAXN];
Point row[MAXN][MAXN];
int headc[MAXN],tailc[MAXN];
Point col[MAXN][MAXN];
inline Point getPointR(reg int i,reg int j){
return Point(2*sumy[j],1ll*sumy[j]*sumy[j]-f[i][j]);
}
inline ll getValR(const Point& p,reg int i,reg int j){
return -((p.y-p.x*sumy[j-1])-x[i]*y[j]+1ll*sumy[j-1]*sumy[j-1]);
}
inline Point getPointC(reg int i,reg int j){
return Point(2*sumx[i],1ll*sumx[i]*sumx[i]-f[i][j]);
}
inline ll getValC(const Point& p,reg int i,reg int j){
return -((p.y-p.x*sumx[i-1])-x[i]*y[j]+1ll*sumx[i-1]*sumx[i-1]);
}
int main(void){
reg int t=read();
while(t--){
n=read();
for(reg int i=1;i<=n;++i)
x[i]=read();
x[n+1]=0;
for(reg int i=1;i<=n;++i)
y[i]=read();
y[n+1]=0;
for(reg int i=1;i<=n+1;++i)
sumx[i]=sumx[i-1]+x[i],sumy[i]=sumy[i-1]+y[i];
for(reg int i=0;i<=n;++i)
headr[i]=tailr[i]=0,headc[i]=tailc[i]=0;
for(reg int i=0;i<=n+1;++i)
for(reg int j=0;j<=n+1;++j)
f[i][j]=-inf;
f[0][0]=0;
for(reg int i=1;i<=n+1;++i){
for(reg int j=1;j<=n+1;++j){
Point r=getPointR(i-1,j-1);
while(tailr[i-1]-headr[i-1]>1&&sgn(cross(row[i-1][tailr[i-1]-1]-row[i-1][tailr[i-1]-2],r-row[i-1][tailr[i-1]-2]))<=0)
--tailr[i-1];
row[i-1][tailr[i-1]++]=r;
while(tailr[i-1]-headr[i-1]>1&&sgn(row[i-1][headr[i-1]+1].y-row[i-1][headr[i-1]].y-1.0*sumy[j-1]*(row[i-1][headr[i-1]+1].x-row[i-1][headr[i-1]].x))<0)
++headr[i-1];
f[i][j]=max(f[i][j],getValR(row[i-1][headr[i-1]],i,j));
Point c=getPointC(i-1,j-1);
while(tailc[j-1]-headc[j-1]>1&&sgn(cross(col[j-1][tailc[j-1]-1]-col[j-1][tailc[j-1]-2],c-col[j-1][tailc[j-1]-2]))<=0)
--tailc[j-1];
col[j-1][tailc[j-1]++]=c;
while(tailc[j-1]-headc[j-1]>1&&sgn(col[j-1][headc[j-1]+1].y-col[j-1][headc[j-1]].y-1.0*sumx[i-1]*(col[j-1][headc[j-1]+1].x-col[j-1][headc[j-1]].x))<0)
++headc[j-1];
f[i][j]=max(f[i][j],getValC(col[j-1][headc[j-1]],i,j));
//printf("i=%d j=%d f=%lld\n",i,j,f[i][j]);
}
}
printf("%lld\n",f[n+1][n+1]);
fprintf(stderr,"%.3lf s\n",1.0*clock()/CLOCKS_PER_SEC);
}
return 0;
}
标签:iy,right,sumy,sumx,题解,texttt,chorus,合唱团,left 来源: https://www.cnblogs.com/Lu-Anlai/p/14883170.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
