标签：mathbb begin end cdots 港队 算法 bmatrix 数据结构 vdots

• 写在前面

这两个东西其实并没有什么联系，但是因为都是由 @dd_d 首创的，所以写在一起。

Update：不想新开博客了，所以以后 dd_d 有什么新发明就直接在这里更新了。

---

• 港队线段树

这是一种高效且简便好写的优秀线段树（ 由香港队长发明的 ），拥有良好的均摊复杂度。

在同时需要记录多个标记时，有十分简洁的下传方式，甚至无需标记（ 与标记永久化类似思想，但不完全相同 ）。

实现原理则是充分利用了线段树叶子节点的性质，使其能快速合并信息。

其实港队线段树不难理解，如果你学过线段树，看代码就能完全理解，但是从古至今却只有他一个人想到了这种高妙的办法。

大致算法流程（ 用修改举例，其他同理 ）

void update(...) {
    if(The length of the section is only 1) {
        //Edit the value
        ...
        return ;
    }
    //push_down(...);
    if(Can reach the left section) update(The left son);
    if(Can reach the right section) update(The right son);
}

当遇到实际题目时，如果能充分利用叶子节点的性质，一些情况下可以使码量大大减小，对港队来说 push_down 只是画蛇添足！

• 举个例子：[清华集训2012]序列操作

按照题解思路将式子展开以后，其他操作可以直接套用港队线段树。

询问只需要按照推出来的式子，预处理一下组合数，从叶子向上乘起来即可，式子不写了，可以去题解区看，会比好写很多，且变得完全没有思维难度了。

• 有同学可能会问：为什么复杂度是对的呢？

考虑当询问一定会分为多个区间，参考下图

这些区间上的存储值合并后就是答案。

考虑这些区间的长度有长有短，在询问随机情况下，我们也许只要 \(1\) 个就能获得答案，也许 \(\log(n)\) 次就会获得答案。

仔细推理一下或感性理解一下就能发现，均摊复杂度为单次 \(O(\log n)\)。

至于修改操作，在较好的随机情况下是 \(O(\sqrt{n})\) 级别的，不算很劣，如果仔细的研究数据规模后，可以在比较好条件下达到 \(O(\log(n))\) 甚至 \(O(1)\)。

但是在方便的前提下谁会在意复杂度呢

---

• 马表

这个目前还在理论阶段，没有比较优秀的实践价值。

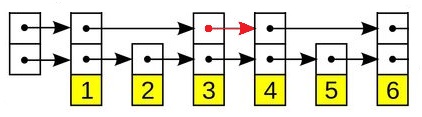
马表，即为带修 st 表，最基础的马表支持期望 \(O(\log n)\) 单点修改，\(O(k)\) 求区间 RMQ，\(k\) 为一个常数，一般的马表 \(k\) 期望为 \(4\sim5\)，优秀的可达到 \(2.64\) 左右大小。

思路就是借用一个 Skip List 的分层概念，修改会在表上多开一个节点，节点过多就重复利用，使节点数控制在一定范围内，查询就在每层上查询。

可以参考图片理解，红色箭头表示一次修改。

相比线段树，马表就有很大优化空间，修改时一些点可以只先在高层打标记，询问时下传到下层，实测所用时间比线段树的 \(\frac{1}{2}\) 还略快。

并且 st 表能维护的内容马表都能维护，并且可以可持久化，十分优秀。

• ex马表

带修带插入的马表，在马表基础上再倍增分块，插入在最顶层，查询再向下新建，小块暴力修改，过大后暴力 split。

但是 \(k\) 能被卡的非常大，可以搞一个估价函数，为块数在再乘一个指数函数，通常取 \((\sqrt{2})^x\)，超过一定之后层与层之间 shuffle 一下，再重建层与层之间的边，在随机数据下跑的飞快。

先考虑插入的每个数字大小和位置都是随机的，即随机到每一块的概率是 \(O(\log n)\) 的，也就是说，期望 \(O(\log^2 n)\) 次会有 \(\frac{\log_2 n}{\log_k n}\) 次 split（ \(k\) 是期望层数 ），因此 split 的总复杂度为 \(O(\frac{q}{\log_k n})\)，不会对马表总复杂度产生影响。

然后是重构，由 split 平衡后，至少要 \(\log n\times tn\) 次才会重构，\(t\) 取决于估价函数的优劣，大概是 \(0.23\sim0.61\)。总复杂度为\(\frac{q}{\log n\times tn}\times n\log n\)，为 \(O(\frac{q}{t})\)，上限约为 \(O(4.236\times q)\)，同样小于朴素马表。

做法似乎十分暴力，但复杂度同样正确。

删除也可以按照这个思路，块内少了就 merge，不平衡就重构，复杂度同理。

ex马表也同马表一样，st 表能维护的都能维护。

• 马表的其他用处

马表可用范围很广，能套用其他数据结构，可以在马表上倍增，或是用马表优化建图，但由于还是理论数据结构，这里就不展开了。

---

• 港队矩乘

首先考虑原来矩阵乘法的式子：

\[\begin{bmatrix} a_{1,1}&\cdots&a_{1,k}\\ \vdots&\ddots&\vdots\\ a_{n,1}&\cdots&a_{n,k}\\ \end{bmatrix} \times \begin{bmatrix} b_{1,1}&\cdots&b_{1,m}\\ \vdots&\ddots&\vdots\\ b_{k,1}&\cdots&b_{k,m}\\ \end{bmatrix} = \begin{bmatrix} c_{1,1}&\cdots&c_{1,m}\\ \vdots&\ddots&\vdots\\ c_{n,1}&\cdots&c_{n,m}\\ \end{bmatrix} \]

先对于每个数考虑它对最终矩阵的贡献，例如 \(a\) 中一个数，它就会对 \(c\) 中同一行的数产生贡献。

因此可以枚举 \(a\) 中每个数，这个贡献就为 \(a_{i,j}\times\begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\) 再加到 \(\begin{bmatrix}c_{i,1}&\cdots&c_{i,m}\end{bmatrix}\) 上。

这里大家可能很疑惑，这不就是矩阵乘法换了个形式表达吗，不能说十分相似，只能说一模一样。

接下来就是港队的操作时间了，考虑怎么将计算过程简化，因为 \(a,b\) 贡献不独立，想想有没有奇怪的打 tag 方法。定义新运算 \(\begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes a_{i,j}\)，先不管这个式子实际意义，但是从形式上可通过原式可以发现：

\[\begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes x + \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes y = \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix}\boxtimes (x\boxplus y) \]

同样你可能也会看着这个式子很疑惑，这不就是矩阵乘常数吗，不能说十分相似，只能说一模一样。

现在不考虑把算出来的值往 \(c\) 里拍，而是直接通过这种新运算把 \(c\) 表示出来，这个 \(\cup\) 表示把每个行矩阵依次拼成一个矩阵。

\[\bigcup_{j=1}^{k} \left( \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \boxtimes \left( \boxplus_{i=1}^{n} a_{i,j} \right) \right) \]

现在考虑如果每个运算时间复杂度为 \(\mathcal{O}(1)\) 的话，这个式子已经做到 \(\mathcal{O}(n^2)\)，但是事实却不是这样，\(\boxtimes\) 是 \(\mathcal{O}(n)\)

你可能也会看着这堆操作很疑惑，这不就是原矩乘的问题吗，不能说十分相似，只能说一模一样。

但是这种描述方式就能做出一些变形，例如这样：

\[\bigcup_{j\in \mathbb{S}} \boxtimes_{p_i} \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} , p_i\in \mathbb{P} \]

仅仅求这个式子的复杂度和质数分布就已经是呈线性关系的了，也就是说，我们最多只能在复杂度上乘 \(\frac{1}{\log n}\)，并且这个 \(\mathbb{S}\) 甚至只能枚举，变劣了吗？真的吗？

考虑去找 \(p_i\) 对应的 \(\mathbb{S}\)

\[\begin{aligned} \mathbf{Original} &= \bigcup_{j\in \mathbb{S}} \left( \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \boxtimes p_i \right) \\ &= \left( \bigcup_{j\in \mathbb{S}} \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \right) \boxtimes p_i \\ &= \left( \overline{\bigcup_{j\not\in \mathbb{S}}} \begin{bmatrix}b_{j,1}&\cdots&b_{j,m}\end{bmatrix} \right) \boxtimes p_i \\ \end{aligned} \]

\[\begin{aligned} \mathbf{\sum Original} &= \sum \begin{bmatrix} b_{1,1}&\cdots&b_{1,m}\\ \vdots&\ddots&\vdots\\ b_{t\in\mathbb{S},1}=0&\cdots&b_{t\in\mathbb{S},1}=0\\ \vdots&\ddots&\vdots\\ b_{k,1}&\cdots&b_{k,m}\\ \end{bmatrix} \boxtimes p_i \\ &= \sum_{i=1}^{|\mathbb{P}\cup[x\le V]|} (-1)^i \left( \begin{bmatrix} b_{1,1}&\cdots&b_{1,m}\\ \vdots&\ddots&\vdots\\ b_{t\in\mathbb{S},1}=0&\cdots&b_{t\in\mathbb{S},1}=0\\ \vdots&\ddots&\vdots\\ b_{k,1}&\cdots&b_{k,m}\\ \end{bmatrix} \boxtimes \left( \gcd\limits_{j\in \mathbb{S},|\mathbb{S}|\le i}^j p_j \right) \right) \\ &= \sum_{i=1}^{|\mathbb{P}\cup[x\le V]|} (-1)^i \begin{bmatrix} b_{1,1}\boxplus G&\cdots&b_{1,m}\boxplus G\\ \vdots&\ddots&\vdots\\ b_{t\in\mathbb{S},1}=0&\cdots&b_{t\in\mathbb{S},1}=0\\ \vdots&\ddots&\vdots\\ b_{k,1}\boxplus G&\cdots&b_{k,m}\boxplus G\\ \end{bmatrix} , G=\gcd\limits_{j\in \mathbb{S},|\mathbb{S}|\le i}^jp_j \\ &= \sum_{i1=1}^{n} \sum_{j1=1}^{n} \sum_{i2=1}^{n} \sum_{j2=1}^{n} \begin{bmatrix} b_{1,1}\boxplus g(D)&\cdots&b_{1,m}\boxplus g(D)\\ \vdots&\ddots&\vdots\\ b_{k,1}\boxplus g(D)&\cdots&b_{k,m}\boxplus g(D)\\ \end{bmatrix} , g(x)=\prod\limits_{i\in\mathbb{P},i|x}i,D=\gcd(a_{i1,j1},a_{i2,j2}) \\ &= \sum_{i=1}^{cnt} \begin{bmatrix} b_{1,1}\boxplus g(D)&\cdots&b_{1,m}\boxplus g(D)\\ \vdots&\ddots&\vdots\\ b_{n,1}\boxplus g(D)&\cdots&b_{n,m}\boxplus g(D)\\ \end{bmatrix} \\ &= \sum_{i=1}^{cnt} \begin{bmatrix} b_{1,1}\boxplus g(B)&\cdots&b_{1,m}\boxplus g(D)\\ \vdots&\ddots&\vdots\\ b_{n,1}\boxplus g(D)&\cdots&b_{n,m}\boxplus g(D)\\ \end{bmatrix} \end{aligned} \]

懒了，就把后面的所有有用的推导都放这了。

第一部分感觉上非常无用，又将式子变回去了，但这个打 tag 方式从行矩阵扩展到矩阵，就能用于解决这个根本问题了。

全集的价值可以直接算出来，子集 \(\mathbb{S}\) 可以通过每个 \(p_i\) 建一个链表快速求出。

由于 \(\sum\limits_{x\in\mathbb{P}}^{x\le n} \frac{1}{x} = \ln(\ln n) + \mathcal{O}(1)\)（为方便后面就写作 \(\log V\) 了），求 \(S\) 部分复杂度 \(\mathcal{O}(n\log^2 V)\)，其余计算部分复杂度为 \(\mathcal{O}(n^2\log V)\)。

但是真的解决了吗？真的吗？你觉得呢？

实际上很好发现复杂度瓶颈在求 \(p_i\)，只能做到 \(\mathcal{O}(V)\)，原式也非积性函数。

后面几步推导就完全解决了这个问题，通过 \(\gcd\) 的转化，就不需要直接求 \(p_i\) 了，还能优化一定常数。

但是要注意一个点，就是新定义运算的原意义是打 tag，是不同于简单的加或乘的，不然理解其中几步的推导可能会出现偏差。

处理掉不存在的行，然后可以通过预处理区间 \(\gcd\) 优化了求答案过程。

dd_d 现在万事缠身，没有造什么题，不过可以自己去找一些 dp 转成矩乘用这个方法优化试试。

---

• 特别鸣谢 @Freedom_King 的帮助和支持。

标签：mathbb,begin,end,cdots,港队,算法,bmatrix,数据结构,vdots
来源： https://www.cnblogs.com/jur-cai/p/16596771.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。