ICode9
精准搜索请尝试： 精确搜索
首页
编程语言>
数据库
系统相关
互联网
其他分享
Python
Java
JavaScript
android
PHP
首页 > 其他分享> 文章详细

一场考试 —— 数学小专场

2021-05-03 21:03:45  阅读：125  来源： 互联网

标签：专场 ch return int 数学 ans include 考试 mod


简要赘述

良心出题人 \(zhx\) ，暴力的分给定十分充足，足足有 \(200+\) 题目也比较水。

预计得分 ： \(310\)
实际得分 ： \(280\)
\(100 + 30 + 100 + 50\)
\(rank \ \ 5/83\)

T1

高精度取膜

【\(solution\)】 : 直接类比读入取模，我们用字符串储存，然后直接 \(*10\) 取模即可

signed main() {
	string s ; cin >> s ; 
	int y = read() , ret = 0; 
	for(qwq int i = 0 ; i < s.size() ; i++) 
	ret = (ret * 10 + (s[i] - '0')) % y ; 
	printf("%lld\n" , ret) ; 
 	return 0 ; 
}

T2

用 \(m\) 种不同的 \(1\times 1\) , \(2\times 2\) 的两类方块 (这两类方块都有 \(m\) 种) 用这些正方形的块来覆盖 \(2\times n\) 的长方形 。 \(n\leq 10^ 9\)

【\(solution\)】 :
我们有显然的递推式 \(f_i = m^3\times (f_{i - 1} + 2\times f_{i -2})\)

signed main() {
	n = read() , m = read() ; 
	f[0] = 1 ; f[1] = m * m * m ; 
	for(qwq int i = 2 ; i <= n ; i ++) 
	f[i] = f[i - 2] * 2 * m * m * m + f[i - 1] * m * m * m ; 
	printf("%lld\n" , f[n]) ; 
 	return 0 ;
}

我们发现 \(n\) 特别的大。并且我们发现 \(f_i\) 可以由 \(f_{i-1}\) 和 \(f_{i-2}\) 转移而来， 和斐波那契数列数列一样，我们考虑用矩阵加速。则就有

\[\begin{bmatrix} f_{i - 1} & f_{i - 2} \end{bmatrix} \ast M = \begin{bmatrix} f_{i} & f_{i - 1} \end{bmatrix} \]

则我们就能够得到

\[M = \begin{bmatrix} m^3 & 1\\ 2\times m^3 & 0 \end{bmatrix} \]

当时在考试上写矩阵加速的我，傻逼的将初始化矩阵写翻了。

\(Code\)

/*
By : Zmonarch
知识点：
*/
#include <bits/stdc++.h>
#define int long long
#define qwq register
#define inf 2147483647
using namespace std ;
const int kmaxn = 1e6 + 10 ;
const int kmod = 1e9 + 7 ;
inline int read() {
	int x = 0 , f = 1 ; char ch = getchar() ;
	while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
	while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
	return x * f ;
}
int n , m ; 
int f[kmaxn] ; 
struct Matrix {
	int a[3][3] ; 
	Matrix() {memset(a , 0 , sizeof(a)) ;}
} ; 
// f[i] = f[i - 2] * 2 * m ^3 + f[i - 1] * m ^ 3 
Matrix operator ^ (const Matrix &m1 , const Matrix &m2) 
{
	Matrix m3 ; //m3.n = m1.n , m3.m = m2.m ; 
	for(qwq int i = 1 ; i <= 2 ; i++) 
 	 for(qwq int k = 1 ; k <= 2 ; k++) 
  	  for(qwq int j = 1 ; j <= 2 ; j++)
	     m3.a[i][j] = (m3.a[i][j] + m1.a[i][k] * m2.a[k][j]) % kmod ;
	return m3 ;
}
Matrix quick(Matrix a , int b) {
	Matrix ret ; 	
	for(qwq int i = 1 ; i <= 2 ; i++) ret.a[i][i] = 1 ;  
	while(b) 
	{
		if(b & 1) ret = ret ^ a; 
		a = a ^ a ; 
		b >>= 1 ; 
	}
	return ret ; 
}
signed main() {
	n = read() , m = read() ; 
	Matrix base ; //base.m = base.n = 2 ;
	base.a[1][1] = m % kmod * m % kmod * m % kmod ; 
 	base.a[1][2] = 1 ; 
 	base.a[2][1] = 2 * m % kmod * m % kmod * m % kmod; 
 	base.a[2][2] = 0 ; 
	Matrix ans ; 
	ans.a[1][1] = m % kmod * m % kmod * m % kmod  ; ans.a[1][2] = 1;
	ans = ans ^ quick(base , n - 1) ;
	printf("%lld\n" , ans.a[1][1]) ;   
	return 0 ;
}

T3

求解 \(x^{C_{n}^m} \ \ mod \ \ 1000003471\)

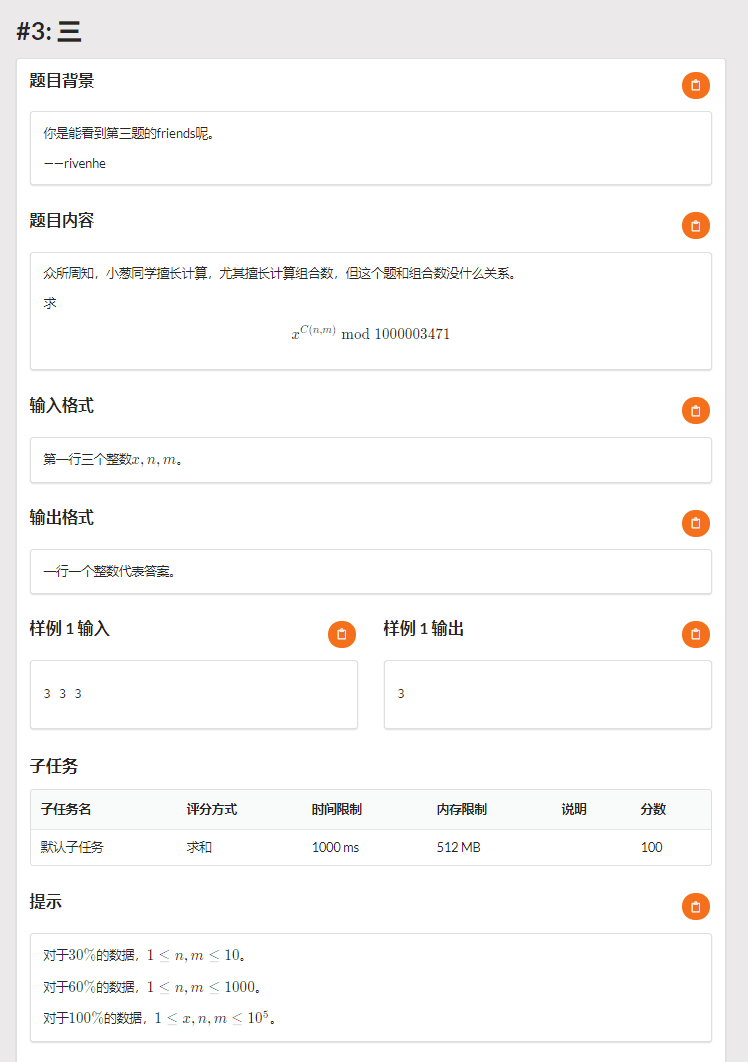
https://images.cnblogs.com/cnblogs_com/Silymtics/1892671/o_210503101023T3.png
哈哈哈，从 \(szt\) 那里嫖来的。

【\(solution\)】:
我们用 \(mod = 1000003471\) 写这个数太麻烦了，以 \(mod\) 代表一下。
我们发现 \(mod\) 是一个质数，我们就能知道我们可以用欧拉定理优化一波
\(x^{C_{n}^{m} \ \ mod \ \ \varphi(mod)}\)
\(\varphi(mod)\) 我们发现这玩意不是个质数。

两种方法

  • 1000003470 可以分解为 \(2×3×5×53×677×929\)
    我们发现其实这个也就能将其搞一下 \(a\text{%} 2 = 0 ， a \text{%}5 = 0 \dots a\text{%}929 = 0\) 我们也就能够得到 \(6\) 个同余方程，我们用中国剩余定理莽上，就能够求解了。

std 干得

  • 我们发现这是一个 \(exlucas\) 定理的板子，我们直接莽上。

我干得

/*
By : Zmonarch
知识点:欧拉定理，扩展卢卡斯定理
*/	
#include <bits/stdc++.h>
#define int long long
#define qwq register
#define inf 2147483647
using namespace std ;
const int kmaxn = 1e6 + 10 ;
const int kmod = 1000003471 ;
inline int read() {
	int x = 0 , f = 1 ; char ch = getchar() ;
	while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
	while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
	return x * f ;
}
int tot ; 
int c[kmaxn] , d[kmaxn] , b[kmaxn]; 
/*int eular(int p) {
	int phi = p ; 
	for(int i = 2 ; i <= sqrt(p) ; i++) 
	{
		if(p % i == 0) 
		{
			phi = phi / i * (i - 1) ;
			while(p % i == 0) p /= i ; 
		}
	}
	if(p > 1) phi = phi / p * (p - 1) ; 
	return phi ; 
}*/
inline int Qpow(int a,int b, qwq int mod) {
	int ans = 1;
	while (b) {
		if (b & 1) ans = ans * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return ans;
}
inline int ExGCD (int a, int b, int &x, int &y) {
	if (!b) {x = 1, y = 0;return a ;}
	int d = ExGCD (b, a % b, x, y);
	int tmp = x;
	x = y;
	y = tmp - (a / b) * y;
	return d;
}
inline int Inv (int a, int mod) { 
	int x = 0, y = 0;
	ExGCD (a, mod, x, y);
	return (x % mod + mod) % mod;
}
inline int Calc (int n, int p, int pk) {
	if (n == 0) return 1;
	int ans = 1;
	for (qwq int i = 1; i <= pk; i ++) 
	if (i % p) ans = ans * i % pk;
	ans = Qpow (ans, n / pk, pk); 
	for (qwq int i = 1; i <= n % pk; i ++) 
    	if (i % p) ans = ans * i % pk;
	return ans * Calc (n / p, p, pk) % pk;
}
inline int C (int n, int m, int p, int pk) {
	if (n == 0 || m == 0 || n == m) return 1;
	if (n < m) return 0;
	int nn = Calc (n, p, pk), mm = Calc (m, p, pk), nm = Calc (n - m, p, pk), cnt = 0, k = n - m;
	while (n) n /= p, cnt += n;
	while (m) m /= p, cnt -= m;
	while (k) k /= p, cnt -= k;
	return nn * Inv (mm, pk) % pk * Inv (nm, pk) % pk * Qpow (p, cnt, pk) % pk;
}
inline int CRT () { 
	int M = 1, ans = 0;
	for (qwq int i = 1; i <= tot; i ++) M *= c[i];
	for (qwq int i = 1; i <= tot; i ++) d[i] = Inv (M / c[i], c[i]);
	for (qwq int i = 1; i <= tot; i ++) ans += b[i] * (M / c[i])  * d[i];
	return (ans % M + M) % M;
}
inline int ExLucas (int n, int m, int p) {
	int tmp = sqrt (p);
	for (qwq int i = 2; i <= tmp && p >= 1; i ++) 
	{ 
		int pk = 1;
		while (p % i == 0) p /= i, pk *= i;
		if (pk > 1) b[++ tot] = C (n, m, i, pk), c[tot] = pk;
	}
	if (p > 1) b[++ tot] = C (n, m, p, p), c[tot] = p;
	return CRT() ; 
}
signed main() {
	//int p = Eular(kmod) ; 我为什么还要筛一遍
	int p = kmod - 1; //质数的话就是 \varphi(n) = n - 1 
	int x = read() , n = read() , m = read() ; 
	int k = ExLucas(n , m , p) ; // C（n ,m） % p  
	//printf("%lld\n" ,k) ; 
	int ret = Qpow(x , k , kmod) ; 
	printf("%lld" , ret) ; 
 	return 0 ;
}

T4

给定 \(n\) 个数 \(a_i\)，求解使得 \(a_i = \gcd(x , y + i - 1)\) 成立的任意 \(x,y\) 、

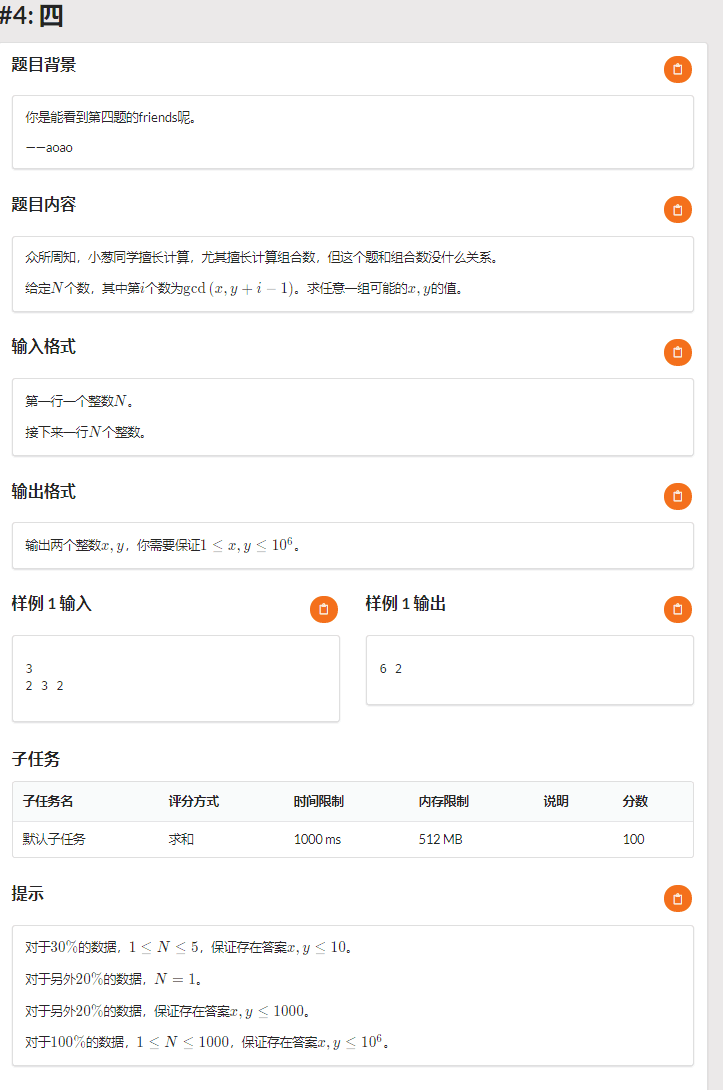
【\(solution\)】 ；

  • 暴力 ： 我们可以直接枚举 \(x,y\) 看一下是否能够成立 ， 你能得到 \(30\) 分。
    我们特判一下 \(n = 1\) 的时候，直接输出那个数，我们能得到 \(20\) 分。
int gcd(int a , int b){ return !b ? a : gcd(b , a % b) ;}
signed main() {
	
	int n = read() ; 
	if(n == 1) { int  num = read() ; printf("%lld %lld" , num , num) ;  ; return 0 ; }
	for(qwq int i = 1 ; i <= n ; i++) a[i] = read() ; 
	for(qwq int i = 1 ; i <= n ; i++) 
	{
		for(qwq int x = 1 ; x <= 10 ; x++) 
		{
			for(qwq int y = 1 ; y <= 10 ; y++) 
			{
				if(a[i] == gcd(x , y + i - 1)) 
				{
					printf("%lld %lld" , x , y) ; 
					return 0 ; 
				}
			}
		}
	}
 	return 0 ;
}
  • 正解：我们可以显然的看出 \(x = lcm_{i = 1}^{n} a_i\) 的，但是 \(y\) 显然不是那么乐观，我们搞搞化简，我们发现这么个玩意

\[(y + i - 1) \equiv 0 (mod \ \ a_i) \]

\[y \equiv n + 1 - i (mod \ \ a_i) \]

我们发现这玩意是个 \(excrt\) , 模板莽上。

这里选择用大数翻倍法 ： \(1.\) 好写， \(2.\) 没写过，练一下。

/*
By : Zmonarch
知识点：
*/
#include <bits/stdc++.h>
#define int long long
#define qwq register
#define inf 2147483647
using namespace std ;
const int kmaxn = 1e6 + 10 ;
const int kmod = 98244353 ;
inline int read() {
	int x = 0 , f = 1 ; char ch = getchar() ;
	while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
	while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
	return x * f ;
}
int a[kmaxn] ; 
int gcd(int a , int b){ return !b ? a : gcd(b , a % b) ;}
void merge(int &n1 , int &m1 , int n2 , int m2) {
	if(m1 < m2) swap(m1 , m2) , swap(m1 , m2) ; 
	while(n1 % m2 != n2) n1 += m1 ; 
	m1 = m1 / gcd(m1 , m2) * m2 ; 
}
signed main() {
	
	int n = read() ; 
	for(qwq int i = 1 ; i <= n ; i++) a[i] = read() ; 
	int x = 1 ; 
	for(qwq int i = 1 ; i <= n ; i++) 
	x = x / gcd(x , a[i]) * a[i] ; 
	int n1 = 0 , m1 = 1 ; 
	for(qwq int i = 1 ; i <= n ; i++) 
	{
		int n2 = ((1 - i) % a[i] + a[i]) % a[i] ; 
		int m2 = a[i] ; 
		merge(n1 , m1 , n2 , m2) ; 
	}
	printf("%lld %lld\n" , x , n1) ; 
 	return 0 ;
}

Std

钟神的代码确定不要一下吗？

\(T1\)

#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
int m;
char s[100010];
int main()
{
	scanf("%s",s+1);
	scanf("%d",&m);
	int l=strlen(s+1);
	long long ans=0;
	for (int a=1;a<=l;a++)
		ans=(ans*10+s[a]-'0')%m;
	printf("%lld\n",ans);
	return 0;
}

\(T2\)

#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
const int mo=1000000007;
int n,m;
struct matrix
{
	int z[2][2];
	matrix()
	{
		memset(z,0,sizeof(z));
	}
}m1,m2;
matrix operator*(const matrix &m1,const matrix &m2)
{
	matrix m3;
	for (int a=0;a<2;a++)
		for (int b=0;b<2;b++)
			for (int c=0;c<2;c++)
				m3.z[a][c] =(m3.z[a][c]+1ll*m1.z[a][b]*m2.z[b][c])%mo;
	return m3;
}
int main()
{
	scanf("%d%d",&n,&m);
	if (n==1) printf("%lld\n",1ll*m*m%mo*m%mo);
	else
	{
		m1.z[0][0]=1;
		m1.z[0][1]=1ll*m*m%mo*m%mo;
		m2.z[0][0]=0;m2.z[1][0]=1;
		m2.z[0][1]=2ll*m*m%mo*m%mo;
		m2.z[1][1]=1ll*m*m%mo*m%mo;
		while (n)
		{
			if (n&1) m1=m1*m2;
			m2=m2*m2;
			n>>=1;
		}
		printf("%d\n",m1.z[0][0]);
	}
	return 0;
}

\(T3\)

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int mo=1000003471;
int pcnt,plist[10];
int x,n,m,C[1000][1000];
int gcd(int a,int b)
{
	if (!b) return a;
	else return gcd(b,a%b);
}
int pow(int a,int b,int mo)
{
	int ans=1;
	while (b)
	{
		if (b&1) ans=1ll*ans*a%mo;
		a=1ll*a*a%mo;
		b>>=1;
	}
	return ans;
}
int get(int n,int m,int p)
{
	C[0][0]=1;
	for (int a=1;a<p;a++)
	{
		C[a][0]=1;
		for (int b=1;b<=a;b++)
		{
			C[a][b]=C[a-1][b-1]+C[a-1][b];
			if (C[a][b]>=p) C[a][b]-=p;
		}
	}
	int ans=1;
	while (n!=0 || m!=0)
	{
		ans=1ll*ans*C[n%p][m%p]%p;
		n/=p;
		m/=p;
	}
	return ans;
}
void merge(int &v1,int &m1,int v2,int m2)
{
	if (m1<m2) swap(v1,v2),swap(m1,m2);
	while (v1%m2!=v2)
		v1+=m1;
	m1=m1/gcd(m1,m2)*m2;
}
int work(int n,int m)
{
	int v1=0,n1=1;
	for (int a=1;a<=pcnt;a++)
	{
		int v2=get(n,m,plist[a]),n2=plist[a];
		merge(v1,n1,v2,n2);
	}
	return v1;
}
int main()
{
	int v=mo-1;
	for (int a=2;a<=v;a++)
		if (v%a==0)
		{
			plist[++pcnt]=a;
			while (v%a==0)
				v/=a;
		}
	scanf("%d%d%d",&x,&n,&m);
	printf("%d\n",pow(x,work(n,m),mo));
	return 0;
}

\(T4\)

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int n,z[1010];
int gcd(int a,int b)
{
	if (!b) return a;
	else return gcd(b,a%b);
}
void merge(int &v1,int &m1,int v2,int m2)
{
	if (m1<m2) swap(v1,v2),swap(m1,m2);
	while (v1%m2!=v2)
		v1+=m1;
	m1=m1/gcd(m1,m2)*m2;
}
int main()
{
	scanf("%d",&n);
	for (int a=1;a<=n;a++)
		scanf("%d",&z[a]);
	int x=1;
	for (int a=1;a<=n;a++)
		x=x/gcd(x,z[a])*z[a];
	int v1=0,m1=1;
	for (int a=1;a<=n;a++)
	{
		int v2=((1-a)%z[a]+z[a])%z[a];
		int m2=z[a];
		merge(v1,m1,v2,m2);
	}
	printf("%d %d\n",x,v1);
	return 0;
}

标签：专场,ch,return,int,数学,ans,include,考试,mod
来源： https://www.cnblogs.com/Zmonarch/p/14728139.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。

关于我们 | 联系我们 | 留言反馈

专注分享技术，共同学习，共同进步。侵权联系[81616952@qq.com]

Copyright (C)ICode9.com, All Rights Reserved.

ICode9版权所有