https://zhuanlan.zhihu.com/p/45223109
高维映射 与 核方法(Kernel Methods)
29 人赞同了该文章
高维映射跟核方法的概念很容易混淆。
高维映射通过将样本从原始空间映射到一个更高维的特征空间,从而解决了低纬下难以解决的问题。
核方法往往跟高维映射配合使用,可以看做是一种技巧,可以通过它来避免这种映射的计算。
下面详细介绍一下这两个概念。
一、高维映射
我们知道,线性回归是用一条直线来拟合数据。但是我们往往会遇到数据并不服从线性分布的情况,比如:
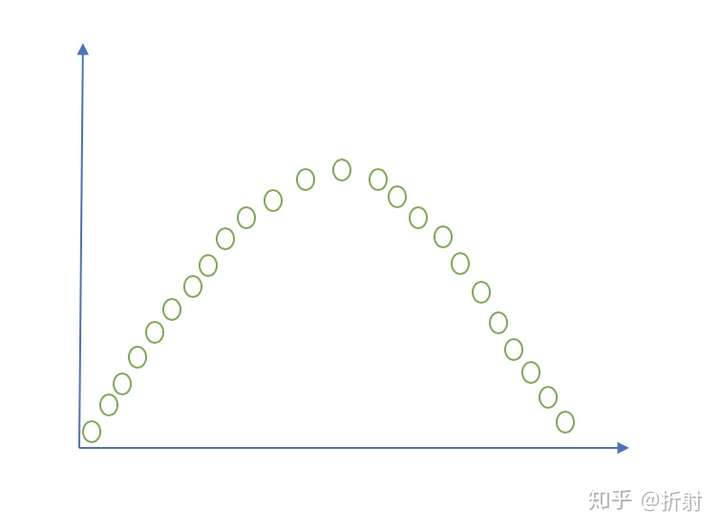
上图这种情况,明显是一个二次函数的分布。如果我们仍旧用线性回归方程 ,那结果是拟合了一条直线,这条直线无论如何也不能完美拟合出这样的二次函数的分布。
于是,我们选择变成一个二次方程来拟合:
它虽然是个二次函数,其实仍然可以看成是一个线性回归。但是现在不是对 的线性回归,而是对于一个更高维度的向量
的线性回归:
令
假如把 输入 看成是一个 1 维的向量,那么
其实就是一个关于
的,更高维度的向量。我们把这种能够把一个向量提升维度的函数,叫做
,
。直观上来讲,在应用了
以后,向量
被拉长了,所以我们把它叫做拉伸函数好了。

拉伸函数是一类函数,表面上看,只要是能把一个向量经过各种修改让它的维度变高,这样的函数都能当成拉伸函数来用。然而并不是这样的,假如你只是单纯地对向量 的分量做线性组合,你会发现实际上并没有提升它的空间,比如我设计一种纯线性组合的拉伸的函数:
将 拉伸为
,那么
,
那么对于提升后的方程, ,乍一看是把2维提升到了5维。其实通过变换以后,相当于还是在对
做线性组合。要选择确确实实提升了维度的拉伸函数。而且,我们的拉伸函数得把原来向量的每个维度都得照顾到。
这里分布是一个二次函数,如果我们遇到了更加复杂的函数,我们依然可以通过选取合适的拉伸函数来变成线性的问题。幸运的是可以证明,只要数据的分布在维度有限的空间上,我们总是能够找到一个更高维度的空间,使得它的分布是线性的。
因此通过高维映射以后,不管原来是不是线性的,总能通过对向量 做拉伸变化,转化成一个高维空间里的线性的回归问题:
二、求解高维映射后的线性方程
如果不做高维映射的话,线性回归的解是:
不明白的可以看看我另外一篇的讲线性回归的,里面包含了推导过程。
折射:线性回归Linear regressionzhuanlan.zhihu.com
我举个例子,帮助你回忆一下里面各个符号的含义。假设我们有5个训练样本 ,每个样本的有2个维度
公式中的 就是把所有训练集拼成的矩阵,每行代表一个训练样本。
是一个对角全为 1 ,其他位置全是0的单位矩阵,
是每个样本输出值拼成的一个向量:

如果我们要对这个公式进行高维映射,也就是说我们对 里的每个样本,也就是每一行的向量都进行了拉伸变换,像这样,我们把拉伸过后的函数叫做
:
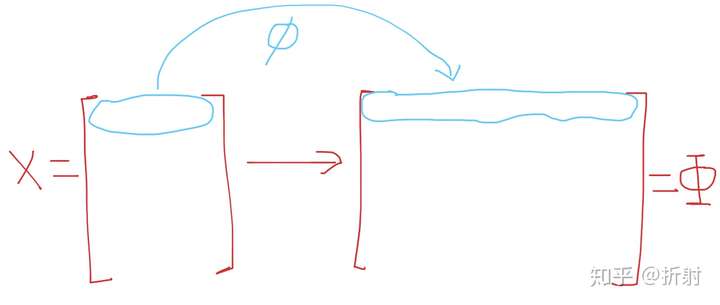
我们用 替换公式里的
,从而得到:
好了,右边全都是已知量,我们已经解出来了这个模型了。
我们做完高维映射之后的线性方程,要如何去预测模型呢?来模拟一下这个过程:
假设,我们现在有 个训练数据,每个数据是
维的。
第一步,我们得计算出 来。
首先把每个数据当成一行,拼成一个矩阵 。然后把矩阵的每一行用拉伸函数做拉伸,从而得到
,最后再套公式求得
:
第二步,下面我们就来利用它做预测了,假如我们要预测 的输出值
,我们又得先对变量
做一次拉伸,得到
,再乘上权重,才能求出它的预测值
:
看看上面的过程中,我们用了多少次拉伸函数。在训练过程中,我们对训练集里面每个样本都用了一次拉伸。在预测的时候,我们又要对预测集里面的每个样本做一次拉伸。现在我告诉你,拉伸函数往往计算量非常大,那么计算这个拉伸显然是一个非常大的开销。
虽然说理论上,因为有限维度的数据必然存在一个拉伸函数将数据映射到高维并且满足线性分布。也就是说必然存在一个完美的拉伸函数。然而,我们往往并不知道到底怎么样的函数才是完美的拉伸函数,选择合适的拉伸函数也是一个非常麻烦的问题。
现在我告诉你,我们有一种取巧的办法。使得我们根本不用计算拉伸函数,有时候甚至你都不需要知道拉伸函数是什么,我们依然能够做预测。这个无比巧妙的简便方法,帮助我们跳过了拉伸的步骤,这个方法就叫做核方法。
三、核函数(Kernel function)
你可能非常迫切地想知道这个巧妙的核方法到底是什么。但是我要在这里卖个关子,不直接告诉你核方法是怎么来的,我们从定义出发一步一步慢慢推导出来。
现在我要转换一下话题,我们先研究研究这个拉伸函数 。我们给它搭配一个“兄弟”,假设向量
是某个跟
同样维度的某个向量,我们对
也同样做拉伸。并且拉伸完之后,我们把这两个向量求内积。
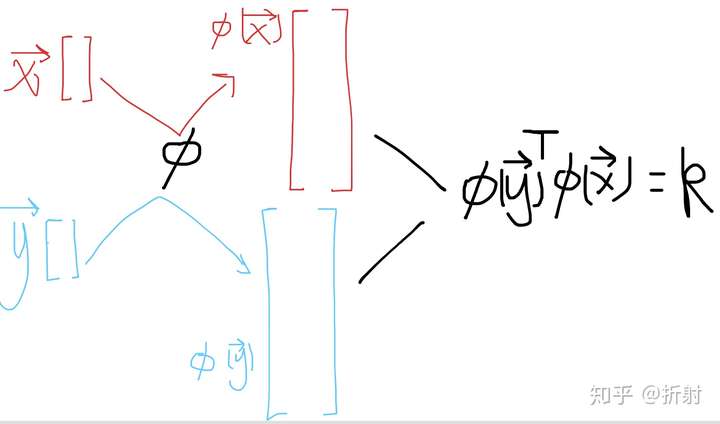
我们知道,两个向量做内积得到的是一个值。这个过程中,我们先是把两个向量拉伸到高维,然后又通过求内积变回一维。
在数学里面,有这样一类函数,它的参数是2个向量,它的输出是一个标量值。它有个特点,就是对于任何相同形状的输入向量 ,它总能改写成这样的形式:
解释一下,这类函数对于任何输入向量 ,它都能改写成分别对两个输入向量做拉伸以后再求内积的表达形式。
这类核函数每个都有各自的表达式,举个例子:
线性核:
多项式核:
注意到,这个表达式里面是不含有拉伸函数的。但是它既然满足核函数的条件,它一定是能改写成两个向量拉伸求内积的形式。
线性核里面隐藏的变换就是做线性拉伸变换(我们之前讨论过,光用线性拉伸是不能解决非线性问题的)。多项式核自然就是做几次方的拉伸变换。换句话说,每一个能被叫做核函数的函数,里面都藏着一个对应拉伸的函数。这些核函数的命名通常也跟如何做拉伸变换有关系。
总结一下,我们现在反了过来,先找满足核函数条件的的表达式,再倒推出一种映射关系。我们选哪个核函数,实际上就是在选择用哪种方法映射。通过核函数,我们就能跳过映射的过程。
四、核方法(Kernel method)
好了,现在我们打定主意,要利用核函数来跳过做映射了。我们假如找到了一个核函数,也就是说我们的拉伸函数也定下来了。我们改写一下核函数的参数,写成这样的形式:
到底要怎么利用呢?先观察一下高维映射以后的模型表达式:
观察一下上面两个公式,你一定能够联想到,肯定要从这个 上面做点文章。没错,我们现在就是要想办法从
里面分离出一个
项来,跟我们的
搭配在一起组成我们的核函数的表达式。
先看看 的计算公式:
在这里跟拉伸项最有关系的一项就是 了,注意这里全都是在做线性组合,
我们我们可以令 ,这里的
我们不知道是什么东西,只知道它是一个向量。
使用 有什么好处呢?
试着把它展开一下,矩阵乘向量的怎么写成求和的形式呢。其实矩阵右乘一个向量,相当于对矩阵的每一列都乘对于向量位置的分量再累加,如图所示:
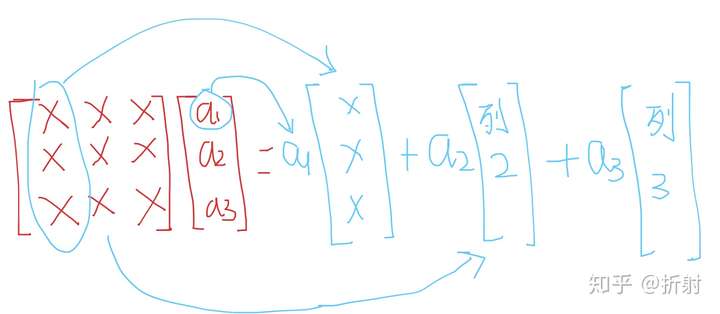
矩阵 是转置过的,它的每一列代表一个训练数据,为了避免混淆,我们用
表示第n个训练数据,可以表示为:
用右边这个替换我们模型里面的 :
看到没有,我们右边已经出现了一个核函数的表达形式了。我们可以直接根据公式 来替换右边,从而得到:
现在的y表达式中,已经不含有拉伸函数项了,这样我们就避开了求拉伸函数的过程。
但是你会发现,我们并不知道 是什么,现在我们就来求这个
。
我们得从求 的表达式开始了,假设我们用最小二乘法做,首先从损失函数开始,同时加入了L2正则项:
如果加了L2正则以后的线性损失函数的公式看不懂,可以去看我写的 机器学习中的正则化,L1 L2正则。 令 ,将
代入到函数中:
求关于 的偏导,并且等于0,可得:
解得:
再看
现在我们把所有的拉伸函数都消除掉了。我们现在就可以用求出来的 来做预测,使用之前我们推出来的公式:
五、总结
在使用机器学习模型做回归或者分类的时候,假如在低维度空间下数据集不好用,那么可以尝试通过把输入的值做高维映射来解决。高维映射不仅仅用于线性回归,包括逻辑回归,还有SVM,尤其是SVM。
由于做高维映射的计算量比较大。当我们遇到需要做高维映射的时候 ,可以通过核方法,把需要学习的模型配出一项来组成
的形式,然后用一个核函数
来替换它,从而消除掉把低维向量往高维映射的过程
。这种替换的技巧就叫做核方法,能够实现替换目的的函数叫做核函数。
利用核方法并非没有缺点。原来的线性模型显然是一种参数化方法,好处是训练完成的模型只需要存储权重向量 。然而在使用了核方法以后,由于我们用训练集替换掉了权重项,因此相当于转化成了非参数化的方法,显然增加了需要存储的数据量,同时每一次做预测都需要用到全部训练数据集。对于参数化和非参数化方法的概念可以看我的另外一篇文章:
折射:机器学习中的正则化,L1 L2正则zhuanlan.zhihu.com
原创,转载请注明出处。
初学者,不可避免出现错误。如果有任何问题,欢迎指正。也欢迎一起交流、讨论。
欢迎关注我的专栏:
https://zhuanlan.zhihu.com/c_1024970634371186688zhuanlan.zhihu.com
标签:拉伸,函数,映射,向量,精解,我们,高维 来源: https://blog.csdn.net/xiaozuo_zhazha/article/details/90340603
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
