标签:后验 KF Sigma 滤波 mu SLAM cases hat check
SLAM学习笔记—后端
-
概述
-
状态估计概率分布的核心思想
未知量(\(x_k\))的后验概率分布 = 似然概率分布 × 未知量(\(x_k\))的先验概率分布
这一等式贯穿全文,请牢牢抓住!
-
运动方程和观测方程
\[\begin{cases} x_k = f(x_{k-1},u_k)+w_k \\\\ z_k=h(x_k)+v_k \end{cases} ,k=1,2,\cdots,N \]
其中\(x_k\overset{def}{=}\{x_k,y_1\cdots,y_m\}\),表示\(k\)时刻所有的未知量(观测位姿,路标位置)
- 运动方程用来估计未知量的先验(预测):先估计出一个先验\(\hat{x}_k\);
- 观测方程用来估计未知量的后验(更新):观测先验值后消除其不确定性,得出确切数值\(x_k\),然后利用似然概率估计观测值\(z_k\),最后利用\(z_k\)校正\(x_k\)得到后者的后验分布\(\check{x}_k\);
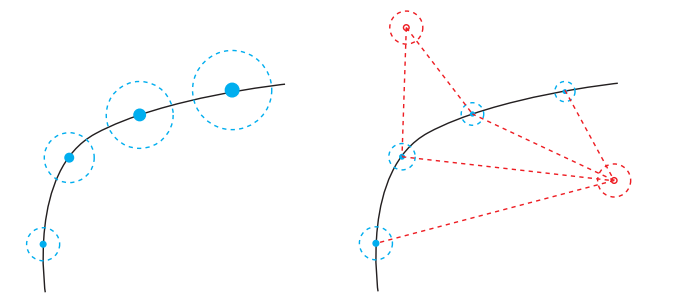
可以看到左图,如果对未知量\(x_k\)做先验估计,由于误差的积累,系统噪音会越来越大。
但是如果通过观测路标点来矫正未知量,对其做后验估计,则误差不会一直增加。
-
线性系统和KF
就是运动方程和观测方程均可以线性表出。
-
-
状态估计概率分布(贝叶斯法则在运动方程和观测方程中的应用)
- \(k\)时刻未知量的后验概率分布记为\(P(\check{x}_k)\),其实际含义为:在已知\(x_0,u_{1:k},z_{1:k}\)的情况下,\(x_k\)的后验概率分布。所以也可以记为\(P(x_k|x_0,u_{1:k},z_{1:k})\);
- \(k\)时刻未知量的先验概率分布记为\(P(\hat{x}_k)\),其实际含义为:在未知\(z_k\)(也就是只已知\(x_0,u_{1:k},z_{1:k-1}\))的情况下,\(x_k\)的先验概率分布。所以也可以记为\(P(x_k|x_0,u_{1:k},z_{1:k-1})\);
- \(k\)时刻的似然概率分布记为\(P(z_k)\),其实际含义为:在已知未知量的先验值的基础上,观测值\(z_k\)的概率分布。所以也可以记为\(P(z_k|x_k)\);
所以,利用贝叶斯法则有:\(P(x_k|x_0,u_{1:k},z_{1:k})\varpropto P(z_k|x_k)·P(x_k|x_0,u_{1:k},z_{1:k-1})\);
-
线性系统和\(\mbox{KF(Kalman Filter)}\)【非主流】
根据条件概率的公式\(P(A|B)\cdot P(B)=P(B|A)\cdot P(A)\)可得:
\[P(x_k|x_o,u_{1:k},z_{1:k})\cdot P(x_0,u_{1:k},z_{1:k}) =P(x_o,u_{1:k},z_{1:k}|x_k)\cdot P(x_k) \]从而引入全概率公式\(P(A_i|B)=\frac{P(B|A_i)\cdot P(A_i)}{\sum P(B)\cdot P(B|A_j)}\propto P(B|A_i)\cdot P(A_i)\)可得:
\[P(x_k|x_o,u_{1:k},z_{1:k}) \propto P(x_o,u_{1:k},z_{1:k}|x_k)\cdot P(x_k) \]通过观察其中的物理含义,也就是“后验=似然×先验”:
-
\(P(x_k|x_o,u_{1:k},z_{1:k})\)代表在修正后得出的位姿分布,也就是后验概率;
-
\(P(x_o,u_{1:k},z_{1:k}|x_k)\)代表在已知分布后如何修正它的最佳分布,也就是似然概率。显然\(k\)时刻的位姿不能影响过去任何一刻的位姿,所以可以简化为\(P(z_k|x_k)\);
-
\(P(x_k)\)代表\(k\)时刻的位姿,本质上就是已知\(1:k-1\)时刻的修正位姿和\(1:k\)时刻的修正输入,得到的当前时刻的位姿分布,所以完整表述应该是\(P(x_k|x_0,u_{1:k},z_{1:k-1})\);
最后为了区分先验概率和后验概率,我们记先验分布为\(\hat{x}_k\)、后验概率为\(\check{x}_k\):
\[P(\check{x}_k|x_o,u_{1:k},z_{1:k})\propto P(z_k|\hat{x}_k)\cdot P(\hat{x}_k|x_0,u_{1:k},z_{1:k-1}) \]我们假设当前状态\(x_k\)只与其前一刻的状态相关,也就是说我们将先验概率分布函数按照\(x_{k-1}\)全概展开:
\[\begin{aligned} P(B|C)&=\sum_{i=1}^{N}P(B|A_iC)·P(A_iC),其中B为\hat{x}_k,A为\check{x}_{k-1} \\ P(\hat{x}_k|x_0,u_{1:k},z_{1:k-1})&=\int P(\hat{x}_k|\check{x}_{k-1},x_0,u_{1:k},z_{1:k-1})·P(\check{x}_{k-1}|x_0,u_{1:k},z_{1:k-1})dx_{k-1} \end{aligned} \]按照线性假设,我们可以去除掉等式中的无关变量(化简等式):
- 对于条件概率(已知\(k-1\)时刻的后验和\(k\)时刻的输入值):由于\(\check{x}_{k-1}\)已经包含了\(u_{1:k-1}\)和\(z_{1:k-1}\),所以可以简化为:\(P(\hat{x}_k|\check{x}_{k-1},u_k)\);
- 对于\(k-1\)时刻后验概率:\(u_k\)不会影响到\(k-1\)的后验,即可化简为:\(P(\check{x}_{k-1}|x_0,u_{1:k-1},z_{1:k-1})\);
马尔科夫链即为:\(P(\hat{x}_k|x_0,u_{1:k},z_{1:k-1},z_{k})\varpropto P(z_k|\hat{x}_k)·\int{P(\hat{x}_k|\check{x}_{k-1},u_k)}P(\check{x}_{k-1}|x_0,u_{1:k-1},z_{1:k-1})dx_{k-1}\)。由于是正比关系,所以我们可以假设运动方程和观测方程均可服从线性表出(\(u_k\)可以忽略):
\[\begin{cases} \hat{x}_k=A_k\check{x}_{k-1}+u_k+w_k \\\\ z_k=C_k\hat{x}_k+v_k \end{cases} ,其中噪声服从高斯分布: \begin{cases} w_k\sim N(0,R_k) \\\\ v_k\sim N(0,Q_k) \end{cases} \]- 记\(k\)时刻\(x_k\)的先验概率分布为\(\hat{X}_k\sim N(\hat{\mu}_k,\hat{\Sigma}_k)\)、后验概率分布为\(\check{X}_k\sim N(\check{\mu}_k,\check{\Sigma}_k)\);
- 由于在观测时必须基于先验数据,所以此时的先验数据将会坍塌,不确定性随之消失,也就是说此时的未知量\(\hat{x}_k=x_k\sim N(x_k,0)\)(是一个常向量),所以可记\(k\)时刻似然概率分布为\(Z_k\sim N(C_kx_k,Q_k)\);
由随机变量函数的概率分布函数计算公式,可以得出:
\[\begin{cases} \hat{\mu}_k=A_k\check{\mu}_{k-1}+u_k \\ \hat{\Sigma}_k=A_k\check{\Sigma}_{k-1}A_k^T+R_k \end{cases} \]然后由于都是服从高斯分布,所以我们可以只对比指数即可(指数就是马氏距离,类似于二次型),对于先验后验的位姿参数\(x_k\)不做符号上的区分,因为已经在均值向量和协方差矩阵上体现出了分布差异,且本质上都是对位姿参数的分布解释,故统一用符号\(x_k\)表示。
\[\begin{aligned} 后验概率分布:&{(x_k-\check{\mu}_k)}^T·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)} \\ 似然概率分布:&{(z_k-C_kx_k)}^T·Q_k^{-1}·{(z_k-C_kx_k)} \\ 先验概率分布:&{(x_k-\hat{x}_k)}^T·\hat{\Sigma}_k^{-1}·{(x_k-\hat{x}_k)} \end{aligned} \]在指数层面观察,后验概率分布 = 似然概率分布 + 先验概率分布,即有如下等式:
\[\small{\begin{aligned} {(x_k-\check{\mu}_k)}^T·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)} &={(z_k-C_kx_k)}^T·Q_k^{-1}·{(z_k-C_kx_k)}+{(x_k-\hat{\mu}_k)}^T·\hat{\Sigma}_k^{-1}·{(x_k-\hat{\mu}_k)} \\ {(x_k^T-\check{\mu}_k^T)}·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)}&={(z_k^T-x_k^TC_k^T)}·Q_k^{-1}·{(z_k-C_kx_k)}+{(x_k^T-\hat{\mu}_k^T)}·\hat{\Sigma}_k^{-1}·{(x_k-\hat{\mu}_k)} \end{aligned}} \]\[\begin{aligned} 等是左边=&{(x_k^T-\check{\mu}_k^T)}·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)} \\=& \underbrace{x_k^T·\check{\Sigma}_k^{-1}·x_k}_{二次项} \underbrace{-x_k^T·\check{\Sigma}_k^{-1}·\check{\mu}_k-\check{\mu}_k^T·\check{\Sigma}_k^{-1}·x_k}_{一次项} \underbrace{+\check{\mu}_k^T·\check{\Sigma}_k^{-1}·\check{\mu}_k}_{常数项} \\ 等式右边=&{(z_k^T-x_k^TC_k^T)}·Q_k^{-1}·{(z_k-C_kx_k)}+{(x_k^T-\hat{\mu}_k^T)}·\hat{\Sigma}_k^{-1}·{(x_k-\hat{\mu}_k)} \\ =& z_k^T·Q_k^{-1}·z_k -z_k^T·Q_k^{-1}·C_kx_k -x_k^TC_k^T·Q_k^{-1}·z_k +x_k^TC_k^T·Q_k^{-1}·C_kx_k \\& +x_k^T·\hat{\Sigma}_k^{-1}·x_k -x_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k -\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·x_k +\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k \\ =& \underbrace{+x_k^TC_k^T·Q_k^{-1}·C_kx_k+x_k^T·\hat{\Sigma}_k^{-1}·x_k}_{二次项} \\ & \underbrace{-z_k^T·Q_k^{-1}·C_kx_k-x_k^TC_k^T·Q_k^{-1}·z_k-x_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k-\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·x_k}_{一次项} \\ & \underbrace{z_k^T·Q_k^{-1}·z_k+\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k}_{常数项} \\=& \underbrace{x_k^T·{(C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1})}·x_k}_{二次项} \\& \underbrace{-[(z_k^TQ_k^{-1}C_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1})·x_k+x_k^T·(C_k^TQ_k^{-1}z_k+\hat{\Sigma}_k^{-1}\hat{\mu}_k)]}_{一次项} \\& \underbrace{z_k^T·Q_k^{-1}·z_k+\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k}_{常数项} \end{aligned} \]所以对应幂次相等原则,可得如下等式:
\[\begin{cases} 二次项:&\check{\Sigma}_k^{-1}=C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1} \\\\ 一次项:& \small{-x_k^T\check{\Sigma}_k^{-1}\check{\mu}_k-\check{\mu}_k^T\check{\Sigma}_k^{-1}x_k = -x_k^T(C_k^TQ_k^{-1}z_k+\hat{\Sigma}_k^{-1}\hat{\mu}_k) -(z_k^TQ_k^{-1}C_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1})x_k} \\\\ 常数项:&\check{\mu}_k^T\check{\Sigma}_k^{-1}\check{\mu}_k=z_k^TQ_k^{-1}z_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1}\hat{\mu}_k \end{cases} \]-
比较二次项系数得后验协方差与先验协方差之间的关系
- 等式两边同时左乘\(\check{\Sigma}_k\):\(I=\check{\Sigma}_kC_k^TQ_k^{-1}C_k+\check{\Sigma}_k\hat{\Sigma}_k^{-1}\);
- 代入卡尔曼增益:\(I=KC_k+\check{\Sigma}_k\hat{\Sigma}_k^{-1}\);
- 整理得协方差关系:\(\check{\Sigma}_k=(I-KC_k)\hat{\Sigma}_k\);
【注】可利用\(\mbox{SWM(Sherman-Morrison-Woodbury)}\)恒等式解出\(K\),该方法可破解循环定义问题。
\[\begin{aligned} &K=\check{\Sigma}_kC_k^TQ_k^{-1}=(C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1})^{-1}C_k^TQ_k^{-1}\\ &由SMW恒等式:AB{(D+CAB)}^{-1}\equiv {(A^{-1}+BD^{-1}C)}^{-1}BD^{-1}\\ &令A=\hat{\Sigma}_k,B=C_k^T,C=C_k,D=Q_k,可得:\\ &K=(C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1})^{-1}C_k^TQ_k^{-1}=\hat{\Sigma}_kC_k^T{(Q_k+C_k\hat{\Sigma}_kC_k^T)}^{-1}\\ &即证:K=\check{\Sigma}_kC_k^TQ_k^{-1}\equiv \hat{\Sigma}_kC_k^T{(Q_k+C_k\hat{\Sigma}_kC_k^T)}^{-1},\small{卡尔曼增益可由先验算得} \end{aligned} \] -
比较一次项系数得后验均值与先验均值之间的关系
- 常数和协方差的转置都是本身:\(-2\check{\mu}_k^T\check{\Sigma}_k^{-1}x_k=-2(z_k^TQ_k^{-1}C_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1})x_k\);
- 取\(x_k\)的系数并转置:\(\check{\Sigma}_k^{-1}\check{\mu}_k=C_k^TQ_k^{-1}z_k+\hat{\Sigma}_k^{-1}\hat{\mu}_k\);
- 等式左右两边同时左乘\(\check{\Sigma}_k\):\(\check{\mu}_k=\check{\Sigma}_kC_k^TQ_k^{-1}z_k+\check{\Sigma}_k\hat{\Sigma}_k^{-1}\hat{\mu}_k\);
- 代入卡尔曼增益和协方差关系:\(\check{\mu}_k=\hat{\mu}_k+K(z_k-C_k\hat{\mu}_k)=\hat{\mu}_k+Kv_k\);
【注】所以该关系的意义就是“后验均值”就是“先验均值”加上一个修正量,而这个修正量就是对观测噪音(误差)做一个卡尔曼增益旋转(左乘为向量旋转,右乘为坐标系旋转)。
总结一下,我们通过定义了一个叫“卡尔曼增益”的中间变量建立起了(1)协方差矩阵的先后验概率关系(2)均值的先后验概率关系。于是我们可以将“后验 = 似然 × 先验”的过程分解为两个步骤:
-
预测(通过前一时刻的后验估计当前时刻的先验)
\[\begin{cases} \hat{\mu}_k=A_k\check{\mu}_{k-1}+u_k \\ \hat{\Sigma}_k=A_k\check{\Sigma}_{k-1}A_k^T+R \end{cases} \]
-
更新(通过卡尔曼增益更新先验从而得到后验)
\[\begin{cases} \check{\mu}_k=\hat{\mu}_k+K(z_k-C_k\hat{\mu}_k) \\ \check{\Sigma}_k=(I-KC_k)\hat{\Sigma}_k \end{cases} \]
-
-
非线性系统和\(\mbox{EKF(Extended Kalman Filter)}\)【对KF扩展至一阶】
推到过程与\(\mbox{KF}\)类似,只是核心思想有些微差异。\(\mbox{EKF}\)是对\(\mbox{KF}\)在\(\check{x}_{k-1}=\check{\mu}_{k-1}\)处和\(\hat{x}_k=\hat{\mu}_k\)的一阶泰勒展开:
\[\begin{aligned} &\begin{cases} \hat{x}_k\approx f(\check{\mu}_{k-1},u_k)+\frac{\part{f}}{\part{\check{x}_{k-1}}}|_{\check{x}_{k-1}=\check{\mu}_{k-1}}·(\check{x}_{k-1}-\check{\mu}_{k-1})+w_k \\ z_k\approx h(\hat{\mu}_k)+\frac{\part{h}}{\part{\hat{x}_k}}|_{\hat{x}_k=\hat{\mu}_k}·(\hat{x}_k-\hat{\mu}_k)+v_k \end{cases} \\\\ &记F= \frac{\part{f}}{\part{\check{x}_{k-1}}}|_{\check{x}_{k-1}=\check{\mu}_{k-1}},H=\frac{\part{h}}{\part{\hat{x}_k}}|_{\hat{x}_k=\hat{\mu}_k} \\\\ &\begin{cases} \hat{x}_k\approx F\underbrace{(\check{x}_{k-1}-\check{\mu}_{k-1})}_{\sim N(0,\check{\Sigma}_{k-1})}+\underbrace{w_k}_{\sim N(0,R)}+\underbrace{f(\check{\mu}_{k-1},u_k)}_{常数项} &\sim \small{N(f(\check{\mu}_{k-1},u_k),F\check{\Sigma}_{k-1}F^T+R_k)} \\\\ z_k\approx H\underbrace{(\hat{x}_k-\hat{\mu}_k)}_{\sim N(0,\hat{\Sigma}_k)}+\underbrace{v_k}_{\sim N(0,Q_k)}+\underbrace{h(\hat{\mu}_k)}_{常数项} &\sim N(h(\hat{\mu}_k),H\hat{\Sigma}_kH^T+Q_k) \end{cases} \end{aligned} \]然后贝叶斯展开并对比幂次系数可得:
\[\begin{cases} \check{\mu}_k=\hat{\mu}_k+K_k(z_k-h(\hat{\mu}_k)) \\\\ \check{\Sigma}_k=(I-K_kH)\hat{\Sigma}_k \end{cases} ,其中K_k为卡尔曼增益\overset{def}{=}\hat{\Sigma}_kH^T{(Q_k+H\hat{\Sigma}_kH^T)}^{-1} \]
标签:后验,KF,Sigma,滤波,mu,SLAM,cases,hat,check 来源: https://www.cnblogs.com/SimbaWang/p/16646127.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
