标签:dbinom limits dfrac 笔记 times 学习 cdots 2n 卡特兰
卡特兰数(Catalan 数)学习笔记
一、引入
问题 1
由 \(n\) 个 \(+1\) 和 \(n\) 个 \(-1\) 组成的 \(2n\) 项序列 \(a_1,a_2,\cdots,a_{2n}\),求有多少种方案满足其部分和 \(a_1+a_2+\cdots+a_k \ge 0\ (k=1,2,\cdots,2n)\)。
分析
设满足条件的方案数(即答案)为 \(C_n\),不满足条件的方案数为 \(U_n\)。
由 \(n\) 个 \(+1\) 和 \(n\) 个 \(-1\) 组成的序列总数为 \(\dfrac{(2n)!}{n!n!}=\dbinom{2n}{n}\)
那么 \(C_n+U_n=\dbinom{2n}{n}\)
我们只要求出 \(U_n\),就可以得到 \(C_n\)。
因为不满足条件,所以一定存在第一个 \(k\),使得 \(a_1+a_2+\cdots+a_k<0\)。
因为 \(k\) 是第一个,所以 \(a_1+a_2+\cdots+a_{k-1}=0\),且 \(a_k=-1\)。
同时,\(k\) 为奇整数。
我们将前 \(k\) 项的符号取反,剩下的不变,就可以得到一个由 \(n+1\) 个 \(+1\) 和 \(n-1\) 个 \(-1\) 组成的序列,而这个序列和前面不满足条件的序列一一对应(考虑第一个 \(+1\) 个数超过 \(-1\) 的位置,将这个位置及其前面符号取反,就可以得到一个不满足条件的序列)。
那么 \(U_n\) 等于由 \(n+1\) 个 \(+1\) 和 \(n-1\) 个 \(-1\) 组成的序列的个数,即 \(\dfrac{(2n)!}{(n+1)!(n-1)!}=\dbinom{2n}{n+1}\)。
所以 \(C_n=\dbinom{2n}{n}-\dbinom{2n}{n+1}=\dfrac{1}{n+1}\dbinom{2n}{n}\)。
即为第 \(n\) 个卡特兰数。
扩展
若改为 \(n\) 个 \(+1\),\(m\) 个 \(-1\),且 \(n\ge m\),那么有多少种?
分析
同样设满足条件方案数为 \(A_n\),不满足的为 \(U_n\)。
那么 \(A_n+U_n=\dbinom{n+m}{n}\)。
\(U_n=\dbinom{n+m}{n+1}\),所以 \(A_n=\dbinom{n+m}{n}-\dbinom{n+m}{n+1}\)。
问题 2
求以下递推关系的解:
\(C_0=1\)
\(C_n=C_0C_{n-1}+C_1C_{n-2}+\cdots+C_{n-1}C_0=\sum\limits_{k=0}^{n-1}C_kC_{n-k-1}\)
分析
设 \(g(x)=C_0+C_1x+C_2x^2+\cdots+C_nx^n+\cdots\) 为数列 \(C_0,C_1,\cdots,C_n\) 的生成函数。
\[(g(x))^2=C_0C_0+(C_0C_1+C_1C_0)x+(C_0C_2+C_1C_1+C_2C_0)x^2+\cdots+(C_0C_n+C_1C_{n-1}+\cdots+C_nC_0)x^n \\ =\sum\limits_{i=0}^{\infty}C_{i+1}x^i \]故
\[x(g(x))^2=\sum\limits_{i=0}^\infty C_ix^i-C_0=g(x)-C_0 \\ x(g(x))^2-g(x)+1=0 \]解得
\[g(x)=\dfrac{1\pm \sqrt{1-4x}}{2x} \]又
\[\lim\limits_{x\to0^+}g(x)=C_0=1 \\ \lim\limits_{x\to0^+}g(x)=\lim\limits_{x\to0^+}\dfrac{1\pm \sqrt{1-4x}}{2x}=\lim\limits_{x\to 0^+}\dfrac{2}{1\mp\sqrt{1-4x}} \]故 \(g(x)=\dfrac{1-\sqrt{1-4x}}{2x}\)
由牛顿二项式定理,
\[(1+z)^{\frac{1}{2}}=\sum\limits_{k=0}^{\infty}\dbinom{\frac{1}{2}}{k}x^k \]对于 \(k>0\),
\[\dbinom{\frac{1}{2}}{k}=\dfrac{\frac{1}{2}(\frac{1}{2}-1)\cdots(\frac{1}{2}-k+1)}{k!} \\ =\dfrac{(-1)^{k-1}}{2^k}\dfrac{1\times 3\times 5\times\cdots\times(2k-3)}{k!} \\ =\dfrac{(-1)^{k-1}}{2^k}\dfrac{1\times 2\times 3\times 4\times\cdots\times(2k-3)\times(2k-2)}{2\times 4\times\cdots\times(2k-2)\times (k!)} \\ =\dfrac{(-1)^{k-1}}{k\times 2^{2k-1}}\dfrac{(2k-2)}{((k-1)!)^2} \\ =\dfrac{(-1)^{k-1}}{k\times 2^{2k-1}}\dbinom{2k-2}{k-1} \]以 \(-4x\) 代 \(z\),可得
\[\sqrt{1-4x}=1+\sum\limits_{k=1}^{\infty}\dfrac{(-1)^{k-1}}{k*2^{2k-1}}\binom{2k-2}{k-1}(-1)^k4^kx^k \\ =1-2\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\binom{2k-2}{k-1}x^k \]故
\[g(x)=\dfrac{1}{2x}(1-(1-2\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\binom{2k-2}{k-1}x^k)) \\ =\dfrac{1}{2x}2\sum\limits_{k=1}^{\infty}\dfrac{1}{k}\binom{2k-2}{k-1}x^k \\ =\sum\limits_{k=0}^{\infty}\dfrac{1}{k+1}\dbinom{2k}{k}x^k \]即 \(C_n=\dfrac{1}{n+1}\dbinom{2n}{n}\)
即第 \(n\) 个卡特兰数。
二、应用
例 1
问题
有 \(2n\) 个人排列进入剧场,票价 \(5\) 角。其中 \(n\) 个人有 \(5\) 角硬币,另外 \(n\) 个人有一元硬币。初始售票处无零钱。问有多少种排列方法使得每个有一元硬币的人买票时,都有 \(5\) 角找零?
分析
有 \(5\) 角找零的条件为:在任一位置,有 \(5\) 角硬币的人总数大于等于有一元硬币的人个数。
将有 \(5\) 角硬币的人看作 \(+1\),有一元硬币的人看作 \(-1\),那么就转化为引入中的问题 1。答案为第 \(n\) 个卡特兰数。
例 2
问题
对于一个 \(n\times n\) 的正方形网格,从左下角到右上角,每次只能向右或向上走一格,且不能越过对角线,问有多少种走法。
分析
考虑将向右记为 \(+1\),向上记为 \(-1\),那么合法路径的数目就等于满足 \(\sum\limits_{i=1}^{k}a_i \ge 0\ ,k=1,2,\cdots,2n\),即引入中问题 1。
所以答案即为第 \(n\) 个卡特兰数。
例 3
问题
计算包含 \(n\) 个左括号和 \(n\) 个右括号的合法括号序列种数。
合法括号序列定义:
空串为合法序列。
若 A 为合法序列,那么 (A) 为合法序列。
若 A,B 均为合法序列,那么 AB 为合法序列。
分析
显然在任何位置,左括号的个数一定大于等于右括号的个数。
考虑将左括号看作 \(+1\),右括号看作 \(-1\),那么又转化成了引入中的问题 1,答案是第 \(n\) 个卡特兰数。
例 4
问题
计算 \(n\) 个数合法的出栈序列。
分析
法一:将进栈看作 \(+1\),出栈看作 \(-1\),那么就转化成了引入中的问题 1。
法二:
设答案为 \(c_n\)。
显然 \(c_0=1\)。
我们考虑 \(c_n\) 怎么得来。
令最后一个出栈的数为 \(k\)。
那么在 \(k\) 入栈之前,\(1,2,\cdots,k-1\) 共 \(k-1\) 个数已经入栈并出栈了,方案数为 \(c_{k-1}\)。
在 \(k\) 入栈之后,\(k+1,\cdots,n-1,n\) 共 \(n-k\) 个数会入栈并出栈,方案数为 \(c_{n-k}\)。
故总方案数为 \(\sum\limits_{k=1}^n c_{k-1}c_{n-k}=\sum\limits_{k=0}^{n-1}c_kc_{n-k-1}=C_n\)。
转化成引入中的问题 2。
例 5
问题
求将 \(n+2\) 条边的凸多边形用不相交的对角线分割成三角形区域的方案数。
分析
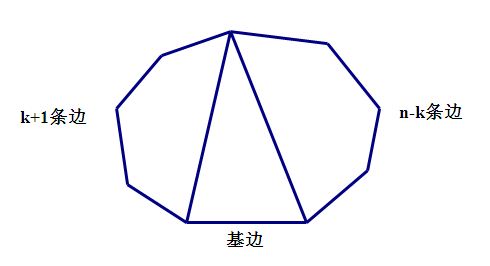
如图,我们选定这个多边形的一条边作为基边,那么在每一种划分中这条基边都是一个三角形区域的边,且这个三角形区域将整个多边形分成了三部分:这个三角形区域,一个含有 \(k+1+1=k+2\) 条边的多边形区域,还有一个含有 \(n+2-k-1-1+1=n-k+1\) 条边的区域。
设含 \(n+2\) 条边的方案数为 \(c_n\)。
那么由分析可知,\(c_n=\sum\limits_{k=0}^{n-1} c_kc_{n-k-1}=C_n\)。
转化为引入中的问题 2。
例 6
问题
求含有 \(n\) 个节点的二叉树的个数。
分析
首先固定一个根节点,左子树有 \(k\) 个节点,那么右子树有 \(n-k-1\) 个节点。
设答案为 \(c_n\),那么 \(c_n=\sum\limits_{k=0}^{n-1}c_kc_{n-k-1}=C_n\)。
转化为引入中的问题 2。
三、公式
- 计算式:\(C_n=\dfrac{1}{n+1}\dbinom{2n}{n}\)。
- 递推式 1:\(C_0=1,C_n=\sum\limits_{k=0}^{n-1}C_kC_{n-k-1}\)
- 递推式 2:\(C_0=1,C_n=\dfrac{4n-2}{n+1}C_n-1\)
- 增长趋势:\(C_n\thicksim\dfrac{4^n}{n^\frac{3}{2}\sqrt{\pi}}\)
标签:dbinom,limits,dfrac,笔记,times,学习,cdots,2n,卡特兰 来源: https://www.cnblogs.com/sysong2006/p/16634272.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
