标签：right Duality Optimization widetilde Convex theta lambda nu left

凸优化

目录

• 凸优化
  • Duality
    • Lagrange function（拉格朗日函数）
      • 定义
    • Lagrange duality function（拉格朗日对偶函数）
      • 定义
      • 性质
      • Lagrange duality function 和 Conjugate function（共轭函数）
        • Conjugate function 定义
        • Lagrange duality function 与 Conjugate function 的关系
    • Lagrange 对偶问题
      • 定义
      • Weak Duality (弱对偶性)
      • Strong Duality (强对偶性)
      • 强对偶性的充分条件：Slater 条件 + convex function
        • 仿射集合
        • 仿射包
        • 相对内点集
        • Slater 条件
        • 修正 Slater 条件
      • 证明Slater 条件 + convex function $ \Rightarrow $ 强对偶性
        • 支撑超平面
        • 超平面分离定理
    • 最优性条件
      • 次优解认证和终止准则
      • 互补松驰性
      • KKT 最优性条件
  • 度量拓扑
    • 内点
      • 定义
    • 开集
      • 定义
      • 性质
    • 闭集
      • 定义
      • 性质
    • 极限点
      • 定义
      • 性质
    • 导集与闭包
      • 定义
      • 性质
    • 内部
      • 定义
      • 性质

目前主要根据 Boyd, Vandenberghe, Convex Optimization来学习凸优化，因为作者理解尚浅，有些理解不足和表达不清的地方，可以在 Convex Optimization 对应知识点进行补充理解， 还请批评指正。

Duality

研究以下标准形式的优化问题，我们称之为原问题：

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{{f_i}\left( x \right) \le 0,i = 1, \ldots ,m}&{}\\ {}&{{h_i}\left( x \right) \le 0,i = 1, \ldots ,p}&{} \end{array} \tag{1} \]

其中，变量 \(x \in D\)，其中定义域 \(D= \cap_{i=0}^{m}domf_{i}\left(x\right)\cap\cap_{i=1}^{p}domh_{i}\left(x\right)\)，假设是非空集合。记原问题的最优值为 $p^{*} $。

Lagrange function（拉格朗日函数）

定义

原问题 \(\left(1\right)\) 的 Lagrange function 为：

\[L\left(x,\lambda,\nu \right)=f_{0}\left(x\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x\right) \]

其中，定义域为 \(dom L= D \times R_{m} \times R_{p}\)，\(\lambda_{i}, \nu_{i}\) 称为第 \(i\) 个不等式约束 \({f_i}\left( x \right) \le 0\) ，第 \(i\) 个等式约束 \({h_i}\left( x \right) \le 0\) 对应的 Langrange 乘子。向量 \(\lambda,\nu\) 称为对偶变量或者是原问题 \(\left(1\right)\) 的 Lagrange 乘子向量。

Lagrange duality function（拉格朗日对偶函数）

定义

原问题 \(\left(1\right)\) 的 Lagrange duality function 为：

\[g\left(\lambda,\nu\right)=\mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu \right)=\mathop {\inf }\limits_{x \in D}\left(f_{0}\left(x\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x\right)\right) \]

其中，定义域为 \(dom g=R_{m} \times R_{p}\)。

性质

• Lagrange duality function 是一族关于 \(\left(\lambda,\nu\right)\) 的一族仿射函数的逐点下确界，对偶函数一定是凹函数。

Reference：

为什么拉格朗日对偶函数一定是凹函数 (逐点下确界)

证明思路：

利用凹函数定义以及 Lagrange duality function 的定义

\[g\left(\theta \lambda_{1}+\left(1- \theta \right)\lambda_{2},\theta \nu_{1}+\left(1- \theta \right)\nu_{2}\right) \geq \theta g\left(\lambda_{1},\nu_{1}\right)+\left(1- \theta \right)g\left(\lambda_{2},\nu_{2}\right) \\ g\left(\lambda,\nu\right)=min\left\{L\left(x_{1},\lambda,\nu \right),L\left(x_{2},\lambda,\nu \right),...,L\left(x_{n},\lambda,\nu \right) \right\} \]

得

\[\begin{align} & g\left( \theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right) \\&=min\left\{ L\left( {{x}_{1}},\theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right),L\left( {{x}_{2}},\theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right),...,L\left( {{x}_{n}},\theta {{\lambda }_{1}}+\left( 1-\theta \right){{\lambda }_{2}},\theta {{\nu }_{1}}+\left( 1-\theta \right){{\nu }_{2}} \right) \right\} \\ & \ge min\left\{ \theta L\left( {{x}_{1}},{{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)L\left( {{x}_{1}},{{\lambda }_{2}},{{\nu }_{2}} \right),\theta L\left( {{x}_{2}},{{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)L\left( {{x}_{2}},{{\lambda }_{2}},{{\nu }_{2}} \right),...,\theta L\left( {{x}_{n}},{{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)L\left( {{x}_{n}},{{\lambda }_{2}},{{\nu }_{2}} \right) \right\} \\ & \ge \theta min\left\{ L\left( {{x}_{1}},{{\lambda }_{1}},{{\nu }_{1}} \right),L\left( {{x}_{2}},{{\lambda }_{1}},{{\nu }_{1}} \right),...,L\left( {{x}_{n}},{{\lambda }_{1}},{{\nu }_{1}} \right) \right\}+\left( 1-\theta \right)min\left\{ L\left( {{x}_{1}},{{\lambda }_{2}},{{\nu }_{2}} \right),L\left( {{x}_{2}},{{\lambda }_{2}},{{\nu }_{2}} \right),...,L\left( {{x}_{n}},{{\lambda }_{2}},{{\nu }_{2}} \right) \right\} \\ & \ge \theta g\left( {{\lambda }_{1}},{{\nu }_{1}} \right)+\left( 1-\theta \right)g\left( {{\lambda }_{2}},{{\nu }_{2}} \right) \end{align} \]

• Lagrange duality function 提供了原问题 \(\left(1\right)\) 的最优值 \(p^{*}\) 的下界，对任意 \(\lambda \geq 0\) 和 \(\nu\) 下式成立
  \[g\left(\lambda,\nu\right)\leq p^{*} \]

证明思路：

利用 Lagrange duality function 的定义，令 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)=p^{*}\) (或者设为原问题的一个可行解)，其中 \(\overset{\sim }{\mathop{x}}\in D\)。

\[\begin{equation} \begin{split} g\left(\lambda,\nu\right)&=\mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu \right) \\&=\mathop {\inf }\limits_{x \in D}\left(f_{0}\left(x\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x\right)\right)\\ & \leq f_{0}\left(\overset{\sim }{\mathop{x}}\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(\overset{\sim }{\mathop{x}}\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(\overset{\sim }{\mathop{x}}\right)\\ {\color{Blue}\because \lambda_{i} \geq 0,f_{i}\left(x\right) \leq 0, \therefore} &\leq f_{0}\left(\overset{\sim }{\mathop{x}}\right)\\ &=p^{*} \end{split} \end{equation} \]

Lagrange duality function 和 Conjugate function（共轭函数）

Conjugate function 定义

\(f:R^{n}\rightarrow R\)，则其共轭函数 \(f^{*}\) 为

\[f^{*}\left(y\right)=\mathop {\sup }\limits_{x \in D}\left\{ y^{T}x-f\left(x\right)\right\} \]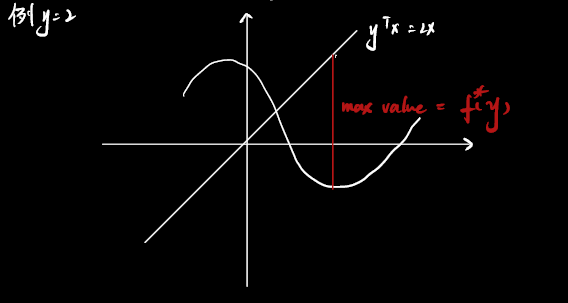

Lagrange duality function 与 Conjugate function 的关系

考虑下面优化问题

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{Ax\leq b}&{}\\ {}&{Cx=d}&{} \end{array} \tag{2} \]

可以转换为

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{Ax-b\leq 0}&{}\\ {}&{Cx-d=0}&{} \end{array} \tag{3} \]

则优化问题\(\left(3\right)\)的 Lagrange duality function

\[ \begin{align*} & g\left( \lambda ,\nu \right)=\underset{x\in D}{\mathop{\inf }}\,L\left( x,\lambda ,\nu \right) \\ & =\underset{x\in D}{\mathop{\inf }}\,\left( {{f}_{0}}\left( x \right)+{{\lambda }^{T}}\left( Ax-b \right)+{{\nu }^{T}}\left( Cx-d \right) \right) \\ & =\underset{x\in D}{\mathop{\inf }}\,\left( {{f}_{0}}\left( x \right)+{{\lambda }^{T}}Ax+{{\nu }^{T}}Cx \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \\ & =-\underset{x\in D}{\mathop{\sup }}\,-\left( {{f}_{0}}\left( x \right)+{{\lambda }^{T}}Ax+{{\nu }^{T}}Cx \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \\ & =-\underset{x\in D}{\mathop{\sup }}\,\left( {{\left( -{{A}^{T}}\lambda -{{C}^{T}}\nu \right)}^{T}}x-{{f}_{0}}\left( x \right) \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \\ & =-f_{0}^{*}\left( -{{A}^{T}}\lambda -{{C}^{T}}\nu \right)-{{\lambda }^{T}}b-{{\nu }^{T}}d \end{align*} \]

其中，下确界问题与上确界问题的等价关系为

\[\underset{x\in D}{\mathop{\inf }}\,S\left( x \right)=-\underset{x\in D}{\mathop{\sup }}\,-S\left( x \right) \]

此关系多数用于计算与证明，如果知道某些函数的共轭函数，可以很方便求对偶函数。

Lagrange 对偶问题

回顾以下两个知识点

• 原问题：

\[\begin{array}{*{20}{c}} {}&{\min {f_0}\left( x \right)}&{}\\ {s.t.}&{{f_i}\left( x \right) \le 0,i = 1, \ldots ,m}&{}\\ {}&{{h_i}\left( x \right) \le 0,i = 1, \ldots ,p}&{} \end{array} \tag{1} \]

其中，变量 \(x \in D\)，其中定义域 \(D= \cap_{i=0}^{m}domf_{i}\left(x\right)\cap\cap_{i=1}^{p}domh_{i}\left(x\right)\)，假设是非空集合。记原问题的最优值为 $p^{*} $。

• 对任意 \(\lambda \geq 0\) 以及 \(\nu\) ，Lagrange duality function 提供了原问题最优值的一个下界

\[g\left(\lambda,\nu\right)\leq p^{*} \]

既然 Lagrange duality function 能提供原问题最优值的一个下界，那很自然就能想到，最接近最优值的下界是什么？或者说最大的下界是多少？我们把求解最接近最优值的下界的问题转换成以下优化问题，并称为原问题\(\left(1\right)\)的 Lagrange 对偶问题。

定义

\[\begin{array}{*{20}{c}} {}&{\max {g\left(\lambda,\nu\right)}}&{}\\ {s.t.}&{\lambda \ge 0}&{}\tag{4} \end{array} \]

其中，变量 \(\left(\lambda,\nu\right)\in dom\text{ } g\)，假设是非空集合。记对偶问题的最优值为 $ d^{*} $。

如果 $g\left(\lambda,\nu\right) = - \infty $，即对偶问题提供一个平凡下界，这样对估计原问题的最优解意义不大。只有当 \(\lambda \ge 0\) 且 \(\left(\lambda,\nu\right)\in dom\text{ } g\)，才能提供一个非平凡下界，我们称这些 \(\left(\lambda,\nu\right)\) 是对偶可行的。如果\(\left(\lambda^{*},\nu^{*}\right)\) 是 Lagrange 对偶问题的最优解，那么称 \(\left(\lambda^{*},\nu^{*}\right)\) 是对偶最优解或者是最优Lagrange乘子。

Weak Duality (弱对偶性)

对 $ \forall \left(\lambda,\nu\right)\in dom\text{ } g$，我们有

\[\begin{equation} \begin{split} g\left(\lambda,\nu\right) \leq p^{*}\\ max \text { }g\left(\lambda,\nu\right) \leq p^{*}\\ d^{*} \leq p^{*}\\ \end{split} \end{equation} \]

！！！注意，到现在为止，我们讨论的优化问题并不局限于凸问题，例如即使原问题不是凸问题，弱对偶性仍然成立

我们把原问题的可行解 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)\) 与对偶问题的可行解 \(g\left(\lambda,\nu\right)\)之间的差值 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)-g\left(\lambda,\nu\right)\) 定义为对偶间隙，而差值 \(p^{*}-d^{*}\) 定义为最优对偶间隙。

既然原问题和对偶问题的最优值存在弱对偶性，自然就想，什么时候不等式取等号？它的充分必要条件什么？退一步，它的充分条件是什么？

Strong Duality (强对偶性)

当最优对偶间隙为零时，即下式成立时

\[d^{*} = p^{*} \]

称强对偶性成立。

强对偶性的充分条件：Slater 条件 + convex function

先介绍几个定义

仿射集合

我们把具有这样形式的线性组合 \(\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{k}x_{k}\)，其中 \(\theta_{1}+\theta_{2}+...+\theta_{k}=1\) 称为 \(x_{1}+x_{2}+...+x_{k}\) 的仿射组合。如果集合\(C\) 包含其中任意点（包括两个点的情况）的放射组合，称该集合 \(C\) 为仿射集合，即 \(\forall x_{1},x_{2},...,x_{k} \in C\)，\(\theta_{1},\theta_{2},...,\theta_{k}\in R\)，且 \(\theta_{1}+\theta_{2}+...+\theta_{k}=1 \)，有 \(\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{k}x_{k}\in C\)。

仿射集合还可以用子空间表示，如果 \(C\) 是一个仿射集合，\(x_{0}\in C\)，则集合

\[V = C-x_{0} =\left\{x-x_{0}|x\in C\right\} \]

为子空间。

证明思路

对 \(\forall v_{1},v_{2}\in V\)，\(\forall\alpha,\beta\in R\)，有 \(v_{1}+x_{0},v_{2}+x_{0} \in C\)

\[\begin{equation} \begin{split} \alpha v_{1}+\beta v_{1}+x_{0}=\alpha \left(v_{1}+x_{0}\right)+\beta \left(v_{2}+x_{0}\right)+\left(1-\alpha-\beta\right)x_{0}&\Rightarrow \alpha v_{1}+\beta v_{1}+x_{0}\in C\\ &\Rightarrow \alpha v_{1}+\beta v_{1}\in C-x_{0}\\ &\Rightarrow \alpha v_{1}+\beta v_{1}\in V\\ \end{split} \end{equation} \]

那么 \(C\) 可以表示为

\[C = V + x_{0} =\left\{v+x_{0}|v\in V\right\} \]

仿射包

我们称由集合 \(C \subseteq R^{n}\) 中的点的所有仿射组合组成的集合为 \(C\) 的仿射包，记为 \(aff \text{ }C\)：

\[C = \left\{\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{k}x_{k}|\forall x_{1},x_{2},...,x_{k} \in C,\theta_{1}+\theta_{2}+...+\theta_{k}=1 \right\} \]

\(aff \text{ }C\) 是包含 \(C\) 的最小的仿射集合。也就是说：如果 \(S\) 是满足 \(C \subseteq S\) 的仿射集合，那么 \(aff \text{ }C\subseteq S\)

相对内点集

我们定义集合 \(D\) 的相对内部为 \(D\) 的仿射包 \(aff \text{ }D\) 的内部，即

\[relint \text{ }D =\left\{x \in D|\exists r >0,s.t.B\left(x,r\right)\cap aff\text{ }D \subseteq D\right\} \]

集合 \(D\) 的相对边界为 \(cl\text{ }D\setminus relint \text{ }D\)，其中 \(cl\text{ }D\) 表示 \(D\) 的闭包。

Slater 条件

存在一点 \(x \in relint \text{ }D\)，使得不等式约束严格成立。

\[\begin{split} \exist x \in relint \text{ }D,s.t. f_{i}(x)&<0,i=1,...,m\\ h_{i}(x)&=0,i=1,...,p \end{split} \]

修正 Slater 条件

当不等式约束函数 \(f_{i}\left(x\right)\) 中有一些仿射函数时，Slater 条件可以进一步弱化。

\[\begin{equation} \begin{split} \exist x \in relint \text{ }D,s.t. f_{i}(x)&\leq 0,i=1,...,k,f_{i}\left(x\right)\text{为仿射函数} \\f_{i}(x)&<0,i=k+1,...,m,f_{i}\left(x\right)\text{为非线性函数} \\h_{i}(x)&=0,i=1,...,p \end{split} \end{equation} \]

则强对偶性的充分条件：（修正）Slater 条件 + convex function

证明Slater 条件 + convex function $ \Rightarrow $ 强对偶性

证明之前，介绍以下定义和定理是有必要的。

支撑超平面

设 \(C \subseteq R^{n}\) 而 \(x_{0}\) 是其边界 $ bd \text{ }C$ 上的一点，即

\[x_{0} \in bd \text{ }C=cl\text{ }C\setminus int \text{ }C \]

如果 \(a \neq 0\)，并且对任意 \(x \in C\) 满足 \(a^{T}x \leq a^{T}x_{0}\) 或 \(a^{T}x \geq a^{T}x_{0}\)，那么称超平面 \(\left\{ x | a^{T}x = a^{T}x_{0}\right\}\) 为集合 \(C\) 在点 \(x_{0}\) 处的支撑超平面。

超平面分离定理

该定理主要想法就是，用超平面或仿射函数将两个不相交的集合分离开来。假设 \(C\) 和 \(D\) 是两个不相交的凸集分离开来，即 \(C \cap D = \varnothing\)，那么存在 \(a \neq 0\) 和 \(b\) 使得对于所有 \(x \in C\) 有 \(a^{T}x \leq b\)，对于所有 \(x \in D\) 有 \(a^{T}x \geq b\)。则超平面 \(\left\{ x | a^{T}x = a^{T}x_{0}\right\}\) 称为集合 \(C\) 和 \(D\) 的分离超平面。

除此之外，定义两个集合

\[g=\left\{ \underbrace{\left( {{f}_{1}}\left( x \right),...,{{f}_{m}}\left( x \right) \right)}_{u},\underbrace{\left( {{h}_{1}}\left( x \right),...,{{h}_{p}}\left( x \right) \right),}_{u}\underbrace{{{f}_{0}}\left( x \right)}_{t}|x\in D \right\} \]

\[\begin{equation} \begin{split} \Alpha =\{\left( u,v,t \right)|\exists x\in D,{{f}_{0}}\left( x \right)&\le {{u}_{i}},i=1,...,m\\ {{h}_{i}} \left( x \right)&\le {{v}_{i}},i=1,...,p,\\ {{f}_{0}} \left ( x \right)&\le t\} \in g +\left(R_{+}^{m} \times \left\{0\right\} \times R_{+}^{p}\right) \end{split} \end{equation} \]

证明思路

假设 \(rank \text{ }A = p\) ，令 \(B=\left\{ \left( 0,0,s \right)\in {{R}^{m}}\times {{R}^{n}}\times R|s<{{p}^{*}} \right\}\)

假设 \(\left( u,v,t \right) \in A \cap B\) ，第一步证明 \(A\) 和 \(B\) 是两个不相交的集合，引入分离超平面

由

\[\begin{equation} \begin{split} \left( u,v,t \right) \in B &\Rightarrow u=0, v=0, \color{Blue}{t<p^{*}}\\ \left( u,v,t \right) \in A &\Rightarrow \exists x\in D,{{f}_{i}}\left( x \right)\le {{u}_{i}}=0,{{h}_{i}}\left( x \right)=0,\color{Blue}{{{f}_{0}}\left( x \right)=t\ge {{p}^{*}}} \end{split} \end{equation} \]

蓝色部分说明 \(A\) 和 \(B\) 是两个不相交的集合。

根据超平面分离定理，存在分离超平面 \(\left( \widetilde{\lambda },\widetilde{\nu },\mu \right)\) ，使得

\[\begin{equation} \begin{split} \exists \left( \widetilde{\lambda },\widetilde{\nu },\mu \right)\ne 0,\alpha \in R\\ {\color{red}\forall\left( u,v,t \right) \in A } &{\color{red}\Rightarrow \left( \widetilde{\lambda },\widetilde{\nu },\mu\right) ^{T} \left( u,v,t \right) \geq \alpha}\\ &{\color{red}\Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) \geq \alpha}\\ {\color{green}\forall\left( u,v,t \right) \in B} &{\color{green}\Rightarrow \left( \widetilde{\lambda },\widetilde{\nu },\mu \right) ^{T} \left( u,v,t \right) \leq \alpha}\\ &{\color{green}\Rightarrow \mu t\leq \alpha} \end{split} \end{equation} \]

第二步在原问题定义域 \(g\) 上构造拉格朗日函数

对于 \(\forall \beta>1,\forall\left( u,v,t \right) \in A ,\exist \left( \beta u,v,\beta t \right)\in A,\left( \widetilde{\lambda },\widetilde{\nu },\mu \right) ^{T} \left( \beta u,v,\beta t \right) \geq \alpha\)，若 \(\widetilde{\lambda }\) 或 \(\mu <0\)，由 \(\beta\) 的无穷大性质，显然可知上述不等式不成立。所以 \(\widetilde{\lambda }\geq 0,\mu \geq0\)。

由 \({\color{green}\forall\left( u,v,t \right) \in B \Rightarrow \mu t\leq \alpha}\) 可知，对所有 \(t<p^{*}\)，都有 \(\mu t\leq \mu p^{*}\)，同时

\[\mu t\leq \mu p^{*}\leq\alpha \]

所以我们可以得到 \(\mu p^{*}\leq\alpha\)。

对 \(\forall\left( u,v,t \right) \in A\)，根据 \(\mu p^{*}\leq\alpha\) ，假设 \(\mu > 0\)（后面会证明一定成立）

\[\begin{equation} \begin{split} {\color{red}\forall\left( u,v,t \right) \in A } &{\color{red}\Rightarrow \left( \widetilde{\lambda },\widetilde{\nu },\mu\right) ^{T} \left( u,v,t \right) \geq \alpha}\\ &{\color{red}\Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) \geq \alpha}\\ &\Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) \geq \mu p^{*}\\ &\Rightarrow \sum_{i=1}^{m}\frac{\widetilde{\lambda }_{i}}{\mu}f_{i}\left(x\right)+\sum_{i=1}^{p}\frac{\widetilde{\nu }_{i}}{\mu}h_{i}\left(x\right)+f_{0}\left(x\right) \geq p^{*}\\ 令L\left(x,\frac{\widetilde{\lambda }_{i}}{\mu},\frac{\widetilde{\nu }_{i}}{\mu}\right)=L\left(x,\lambda,\nu\right)&\Rightarrow L\left(x,\lambda,\nu\right) \geq p^{*}\\ \end{split} \end{equation} \]

因为 \(g \subset A\)，在原问题定义域 \(g\) 上的拉格朗日函数 \(L\left(x,\lambda,\nu\right)=L\left(x,\frac{\widetilde{\lambda }_{i}}{\mu},\frac{\widetilde{\nu }_{i}}{\mu}\right)\geq p^{*}\)，对 \(x\) 取极小值，我们有 \(g\left(\lambda,\nu\right)=\mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu\right)\geq p^{*}\)

第三步证明强对偶性成立

由弱对偶性，

\[g\left(\lambda,\nu\right) \leq p^{*} \]

所以

\[g\left(\lambda,\nu\right) = p^{*} \]

第四步证明 \(\mu > 0\)，这里运用到slater 条件

若 \(\mu = 0\)，假设 \(\widetilde{x}_{0}\in D\) 为满足 slater 条件的一点，所以

\[\begin{equation} \begin{split} {\color{red}\sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(\widetilde{x}_{0}\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(\widetilde{x}_{0}\right)+\mu f_{0}\left(\widetilde{x}_{0}\right) }&\geq 0\\ (\mu=0) \Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(\widetilde{x}_{0}\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(\widetilde{x}_{0}\right)&\geq 0\\ (\widetilde{x}_{0}\in D 为满足 slater 条件的一点,h_{i}\left(\widetilde{x}_{0}\right)=0) \Rightarrow \sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(\widetilde{x}_{0}\right)&\geq 0\\ (\widetilde{x}_{0}\in D 为满足 slater 条件的一点,f_{i}\left(\widetilde{x}_{0}\right)<0,\widetilde{\lambda }_{i}\geq 0) \Rightarrow \widetilde{\lambda }_{i}&= 0 \end{split} \end{equation} \]

由于 \(\left( \widetilde{\lambda },\widetilde{\nu },\mu \right)\ne 0\)，所以 \(\widetilde{\nu }\ne 0\)。对于 \(x\in D\)，有

\[\begin{equation} \begin{split} {\color{red}\sum_{i=1}^{m}\widetilde{\lambda }_{i}f_{i}\left(x\right)+\sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)+\mu f_{0}\left(x\right) }&\geq 0\\ \sum_{i=1}^{p}\widetilde{\nu }_{i}h_{i}\left(x\right)&\geq 0\\ \widetilde{\nu }^{T}\left(Ax-b\right)&\geq 0 \end{split} \end{equation} \]

又因为 \(\widetilde{x}_{0}\in D\) 为满足 slater 条件的一点，且 \(\widetilde{x}_{0}\in int \text{ }D\)，所以

\[\exists \varepsilon ,x=\widetilde{x}_{0}-\varepsilon A^T\widetilde{\nu }\in D,s.t.\widetilde{\nu }^T(A(\widetilde{x}_{0}-\varepsilon A^T\widetilde{\nu })-b)＝-\varepsilon \widetilde{\nu }^TAA^T\widetilde{\nu }\leq0 \]

除非 \(A^{T}\widetilde{\nu } =0\) ，不然总存在 \(D\) 中的点使得 \({\widetilde{\nu }^{T}}\left( Ax-b \right)<0\)。而 \(A^{T}\widetilde{\nu }=0\left(\widetilde{\nu } \ne 0\right)\) 显然与假设 \(rank \text{ }A = p\) 矛盾。

Reference：

证明四 强对偶定理（Strong Duality Theorem） - 知乎 (zhihu.com)

最优性条件

次优解认证和终止准则

回顾以下对偶间隙的定义，我们把原问题的可行解 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)\) 与对偶问题的对偶可行解 \(g\left(\lambda,\nu\right)\)之间的差值 \(f_{0}\left(\overset{\sim }{\mathop{x}}\right)-g\left(\lambda,\nu\right)\) 定义为对偶间隙，而差值 \(p^{*}-d^{*}\) 定义为最优对偶间隙。但我们并不知道为什么引入对偶间隙这个概念。实则对偶间隙提供了我们估计可行解 $ f_{0}\left(\overset{\sim }{\mathop{x}}\right)$ 与最优值 \(p^{*}\) 差值的一个有效手段，这是因为

\[\begin{equation} \begin{split} p^{*}&\geq L\left(x,\lambda,\nu \right)\\ &\geq \mathop {\inf }\limits_{x \in D}L\left(x,\lambda,\nu \right)\\ &= g\left(\lambda,\nu\right)\\ \\ \Rightarrow f_{0}\left(\overset{\sim }{\mathop{x}}\right)-p^{*}&\leq f_{0}\left(\overset{\sim }{\mathop{x}}\right)- g\left(\lambda,\nu\right) \end{split} \end{equation} \]

可以看到，不等式右边为对偶间隙。一对原对偶问题的可行点 \(x\)，\(\left(\lambda,\nu\right)\) 将原问题（对偶问题）的最优值限制在一个区间上：

\[p^{*}\in\left [ g\left(\lambda,\nu\right), f_{0}\left(x\right)\right],d^{*}\in\left [ g\left(\lambda,\nu\right), f_{0}\left(x\right)\right] \]

因此，这一特性可用于迭代求解的终止条件。

设 \(x_{k}\) 为第 \(k\) 轮迭代的原问题可行解，\(\left(\lambda_{k},\nu_{k}\right)\) 为第 \(k\) 轮迭代的对偶可行解，\(k=1,2,...\)，给定要求的绝对精度 \(\varepsilon_{abs}>0\)，那么终止条件为：

\[f_{0}\left(x_{k}\right)- g\left(\lambda_{k},\nu_{k}\right)\leq \varepsilon_{abs} \]

考虑到量纲问题，还可以定义相对误差：

\(if \text{ }g\left(\lambda_{k},\nu_{k}\right)>0:\)

\[\frac{f_{0}\left(x_{k}\right)- p^{*}}{\left |p^{*} \right |}\leq \frac{f_{0}\left(x_{k}\right)- g\left(\lambda_{k},\nu_{k}\right)}{g\left(\lambda_{k},\nu_{k}\right)}\leq \varepsilon_{abs}\\ \]

\(if \text{ } f_{0}\left(x_{k}\right)<0:\)

\[\frac{f_{0}\left(x_{k}\right)- p^{*}}{\left |p^{*} \right |}\leq \frac{f_{0}\left(x_{k}\right)- g\left(\lambda_{k},\nu_{k}\right)}{-f_{0}\left(x_{k}\right)}\leq \varepsilon_{abs}\\ \]

如果原对偶可行对 \(x\)，\(\left(\lambda,\nu\right)\) 的对偶间隙为零，即 \(f_{0}\left(x\right)= g\left(\lambda,\nu\right)\) ，那么 \(x\) 是原问题最优解且\(\left(\lambda,\nu\right)\) 是对偶问题最优解。

可能会有一点疑惑，为什么对偶间隙为零，就是 \(x\)，\(\left(\lambda,\nu\right)\) 就是各自问题的最优解？

我们用反证法，假设 \(x\) 不是原问题最优解，即存在 \(x^{*}\)，使得 \(g\left(\lambda,\nu\right) = f_{0}\left(x\right) > f_{0}\left(x^{*}\right)\)，但由弱对偶性，显然矛盾。同理假设 \(\left(\lambda,\nu\right)\) 不是对偶问题最优解也同样成立。

互补松驰性

由弱对偶性可以得到原问题最优值的一个下界，那我们研究强对偶性，它能得到什么结论或信息？这就是互补松驰性的来源。

\[\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0,i=1,...,m \]

证明思路：

有强对偶性 \(p^{*}=d^{*}\) 可得 \(f_{0}\left(x^{*}\right)=g\left(\lambda^{*},\nu^{*}\right)=L\left(x^{*},\lambda^{*},\nu^{*}\right)\)。这是因为

\[\begin{align*} & g\left( {{\lambda }^{*}},{{\nu }^{*}} \right)=f_{0}^{*}\left( {{x}^{*}} \right) \\ & \ge \underset{\lambda ,\nu }{\mathop{\max }}\,\left( {{f}_{0}}\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{m}{{{\lambda }_{i}}}{{f}_{i}}\left( {{x}^{*}} \right)\left( \le 0 \right)+\sum\limits_{i=1}^{p}{{{\nu }_{i}}}{{h}_{i}}\left( {{x}^{*}} \right) \right) \\ & =\underset{\lambda ,\nu }{\mathop{\max }}\,L\left( {{x}^{*}},\lambda ,\nu \right) \\ & \ge {{f}_{0}}\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{m}{\lambda _{i}^{*}}{{f}_{i}}\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{p}{\nu _{i}^{*}}{{h}_{i}}\left( {{x}^{*}} \right) \\ & \ge inf\text{ }L\left( x,{{\lambda }^{*}},{{\nu }^{*}} \right) \\ & \ge g\left( {{\lambda }^{*}},{{\nu }^{*}} \right) \end{align*} \]

由不等式两边，可以得到

\[\begin{equation} \begin{split} \color{red}{g\left(\lambda^{*},\nu^{*}\right)} &= f_{0}\left(x^{*}\right)\\ &= \mathop {\max }\limits_{\lambda,\nu}\left(f_{0}\left(x^{*}\right)+\sum_{i=1}^{m}\lambda_{i}f_{i}\left(x^{*}\right)+\sum_{i=1}^{p}\nu_{i}h_{i}\left(x^{*}\right)\right)\\ &= \mathop {\max }\limits_{\lambda,\nu}L\left(x^{*},\lambda,\nu \right)\\ &= \color{red}{f_{0}\left(x^{*}\right)+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}\left(x^{*}\right)+\sum_{i=1}^{p}\nu_{i}^{*}h_{i}\left(x^{*}\right)}\\ &= inf \text{ }L\left(x,\lambda^{*},\nu^{*}\right)\\ &= g\left(\lambda^{*},\nu^{*}\right) \end{split} \end{equation} \]

即

\[f_{0}\left(x^{*}\right)=g\left(\lambda^{*},\nu^{*}\right)=L\left(x^{*},\lambda^{*},\nu^{*}\right)=f_{0}\left(x^{*}\right)+{\color{red}\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}\left(x^{*}\right)}+\sum_{i=1}^{p}\nu_{i}^{*}h_{i}\left(x^{*}\right) \]

所以

\[\sum_{i}^{m}\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0\\ \Rightarrow\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0,i=1,...,m \]

KKT 最优性条件

KKT 最优性条件如下

\[\begin{equation} \begin{split} f_{i}^{*}\left(x\right)&\leq0,i=1,...,m\\ h_{i}^{*}\left(x\right)&\leq0,i=1,...,p\\ \lambda_{i}^{*}&\geq0,i=1,...,m\\ \lambda_{i}^{*}f_{i}^{*}\left(x\right)&=0,i=1,...,m\\ \bigtriangledown f_{0}\left ( x^{*} \right )+\sum_{i}^{m}\lambda_{i}^{*}\bigtriangledown f_{i}\left(x^{*}\right)+\sum_{i}^{p}\nu_{i}^{*}\bigtriangledown h_{i}\left(x^{*}\right)&=0\\ \end{split} \end{equation} \]

• 强对偶条件 \(p^{*}=d^{*}\)，\(f_{i}\)，\(h_{i}\) 可微 \(\Rightarrow\) KKT 条件

证明思路

由强对偶条件，显然得到

\[\begin{equation} \begin{split} f_{i}^{*}\left(x\right)&\leq0,i=1,...,m\\ h_{i}^{*}\left(x\right)&\leq0,i=1,...,p\\ \lambda_{i}^{*}&\geq0,i=1,...,m\\ \lambda_{i}^{*}f_{i}^{*}\left(x\right)&=0,i=1,...,m \end{split} \end{equation} \]

又因为

\[\begin{equation} \begin{split} g\left(\lambda^{*},\nu^{*}\right)&=L\left(x^{*},\lambda^{*},\nu^{*}\right)\\ &=inf \text{ }L\left(x,\lambda^{*},\nu^{*}\right) \end{split} \end{equation} \]

若满足 \(g\left(\lambda^{*},\nu^{*}\right)=inf \text{ }L\left(x,\lambda^{*},\nu^{*}\right)\)，需要满足 \(L^{'}\left(x^{*}\right) = 0\)，即

\[\bigtriangledown _{x^{*}} L = \bigtriangledown f_{0}\left ( x^{*} \right )+\sum_{i}^{m}\lambda_{i}^{*}\bigtriangledown f_{i}\left(x^{*}\right)+\sum_{i}^{p}\nu_{i}^{*}\bigtriangledown h_{i}\left(x^{*}\right)=0 \]

• KKT 条件， \(f_{i}\)，\(h_{i}\) 可微 + 凸问题 \(\Rightarrow\) 强对偶条件 \(p^{*}=d^{*}\)

从 KKT 条件可知，\(x^{*}\) 是原问题的可行解，现证明为最优解：

由KKT 条件中 \(\bigtriangledown _{x^{*}} L = \bigtriangledown f_{0}\left ( x^{*} \right )+\sum_{i}^{m}\lambda_{i}^{*}\bigtriangledown f_{i}\left(x^{*}\right)+\sum_{i}^{p}\nu_{i}^{*}\bigtriangledown h_{i}\left(x^{*}\right)=0\) 以及凸问题，可以得到 \(x^{*}\) 是最小值。

又因为 KKT 条件 \(\lambda_{i}^{*}f_{i}^{*}\left(x\right)=0,i=1,...,m\) 可以得到

\[\begin{equation}\begin{split} g\left(\lambda^{*},\nu^{*}\right)&=L\left(x^{*},\lambda^{*},\nu^{*}\right)\\ &=f_{0}\left(x^{*}\right)+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}\left(x^{*}\right)+\sum_{i=1}^{p}\nu_{i}^{*}h_{i}\left(x^{*}\right)\\ &=f_{0}\left(x^{*}\right) \end{split} \end{equation} \]

综上所述，强对偶条件 \(p^{*}=d^{*}\)

度量拓扑

内点

定义

设 \(\left(X,d\right)\) 是度量空间，\(G\) 是 \(X\) 的子集，若存在某个开球 \(U\left(x_{0},r\right)\)，使得 \(U\left(x_{0},r\right)\subset G\)，那么称 \(x_{0} \in G\) 称为 \(G\) 的内点。

开集

定义

若 \(G\) 的每一个点都是 \(G\) 的内点，称 \(G\) 为开集。

性质

• 任意个开集的并集是开集
• 有限个开集的交集是开集

闭集

定义

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，若 \(F\) 的余集 \(F^{c}\) 是开集，称 \(F\) 为闭集。

性质

• \(\varnothing\) 和 \(X\) 是闭集
• 任意个闭集的交集是闭集
• 有限个闭集的并集是闭集

证明思路——利用De Morgen 公式

若 \(\left\{A_{\alpha}:\alpha\in\Lambda\right\}\) 是一族集合，则

（1）\(\left(\cup_{\alpha\in\Lambda}A_{\alpha}\right)^{c}=\cap_{\alpha\in\Lambda}A_{\alpha}^{c}\)

（2）\(\left(\cap_{\alpha\in\Lambda}A_{\alpha}\right)^{c}=\cup_{\alpha\in\Lambda}A_{\alpha}^{c}\)

极限点

定义

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，\(x \in X\) ，若包含 \(x\) 的任意开集都含有不同于 \(x\) 的 \(F\) 的点，则称 \(x\) 为 \(F\) 的极限点。

性质

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，\(x_{0} \in X\) ，则下列条件等价：

• \(x_{0}\) 为 \(F\) 的极限点
• 包含 \(x_{0}\) 任何一个开集都含有 \(F\) 异于 \(x_{0}\) 的无穷多个点（若有限，则在有限个点中取半径 \(min \text{ }d\) 的开球，不满足极限点定义）
• 在 \(F\) 中存在序列 \(x_{n}\)， \(x_{n}\neq x_{0}\)，且 \(\lim_{n\rightarrow \infty }x_{n} = x_{0}\)（注意，一定是 \(x_{n}\neq x_{0}\)，因为极限点要求任意开集都含有不同于 \(x_{0}\) 的点）

导集与闭包

定义

设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，称 \(F\) 的极限点全体为 \(F\) 的导集，记为 \(F^{’}\) 。\(\bar{F}=F\cup F^{'}\) 称为 \(F\) 的闭包。

性质

1. 下列条件等价：

• \(F\) 是闭集
• \(F^{’} \subset F\)
• \(\bar{F} = F\)

2. 设 \(\left(X,d\right)\) 是度量空间，\(F\) 是 \(X\) 的子集，\(x \in X\) ，则下列条件等价：

• \(x \in \bar{F}\)

• \(x\) 的每个开球都包含有 \(F\) 的点

• 存在序列 \(\left\{x_{n}\right\}\)，使得 \(\lim_{n\rightarrow \infty }x_{n} = x_{0}\)（注意，这时不一定是 \(x_{n}\neq x_{0}\)，因为闭包包括\(F\) 本身的点）

内部

定义

设 \(\left(X,d\right)\) 是度量空间，\(G\) 是 \(X\) 的子集，称 \(G\) 的内点全体为 \(G\) 的内部，记为 \(G^{0}\) 。

性质

下列条件等价：

• \(G\) 是开集当且仅当 \(G^{0}=G\)
• \(G^{0}\subseteq G \subseteq \bar G\)（第一个关系 \(G^{0}\subseteq G\)，是因为 \(G\) 可能包含孤立点；第一个关系 \(G \subseteq \bar G\)，是因为 \(\bar G\) 包含了极限点（更形象去理解为边界点，因为内点也是极限点）
• 当 \(G \subset F\) 时，一定有 \(G^{0} \subset F^{0}\)，\(\bar G\ \subset \bar F\)

Reference

黎永锦.泛函分析讲义[M].北京：科学出版社，2011：6-10

标签：right,Duality,Optimization,widetilde,Convex,theta,lambda,nu,left
来源： https://www.cnblogs.com/guanyang/p/16287060.html

本站声明： 1. iCode9 技术分享网（下文简称本站）提供的所有内容，仅供技术学习、探讨和分享；
2. 关于本站的所有留言、评论、转载及引用，纯属内容发起人的个人观点，与本站观点和立场无关；
3. 关于本站的所有言论和文字，纯属内容发起人的个人观点，与本站观点和立场无关；
4. 本站文章均是网友提供，不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属；如您发现该文章侵犯了您的权益，可联系我们第一时间进行删除；
5. 本站为非盈利性的个人网站，所有内容不会用来进行牟利，也不会利用任何形式的广告来间接获益，纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。