[学习笔记]第二次线代战争

2022-01-26 23:05:34 阅读：152 来源： 互联网

\[\color{red}{\text{校长者，真神人也，左马桶，右永神，会执利笔破邪炁，何人当之？}} \\ \begin{array}{|} \hline \color{pink}{\text{The principal is really a god}} \\ \color{pink}{\text{with a closestool on the left and Yongshen on the right}} \\ \color{pink}{\text{holding a sharp pen to pierce the truth}} \\ \color{pink}{\text{Who can resist him? }} \\ \hline \end{array} \\ \begin{array}{|} \hline \color{green}{\text{校長は本当に神であり、左側にトイレ、右側にヨンシェンがあり}} \\ \color{green}{\text{鋭いペンを持って真実を突き刺している。誰が彼に抵抗できるだろうか？ }} \\ \hline \end{array} \\ \begin{array}{|} \hline \color{lightblue}{\text{Le principal est vraiment un dieu}} \\ \color{lightblue}{\text{avec des toilettes à gauche et Yongshen à droite}} \\ \color{lightblue}{\text{tenant un stylo pointu pour percer la vérité}} \\ \color{lightblue}{\text{Qui peut lui résister ? }} \\ \hline \end{array} \\ \begin{array}{|} \hline \color{purple}{\text{Der Direktor ist wirklich ein Gott}} \\ \color{purple}{\text{mit einer Toilette links und Yongshen rechts}} \\ \color{purple}{\text{der einen spitzen Stift hält}} \\ \color{purple}{\text{um die Wahrheit zu durchdringen.}} \\ \color{purple}{\text{Wer kann ihm widerstehen? }} \\ \hline \end{array} \\ \begin{array}{|} \hline \color{cyan}{\text{Principalis deus est, Yongshen a dextris cum latrina}} \\ \color{cyan}{\text{acuto stylo ad perforandum veritatem: quis resistet ei? }} \\ \hline \end{array} \\ \color{red}{\text{对曰：“无人，狗欲当之，还请赐教！”}} \\ \newcommand\brak[1]{\left({#1}\right)} \newcommand\Brak[1]{\left\{{#1}\right\}} \newcommand\d[0]{\text{d}} \newcommand\string[2]{\genfrac{\{}{\}}{0pt}{}{#1}{#2}} \newcommand\down[2]{{#1}^{\underline{#2}}} \newcommand\ddiv[2]{\left\lfloor\frac{#1}{#2}\right\rfloor} \newcommand\udiv[2]{\left\lceil\frac{#1}{#2}\right\rceil} \newcommand\lcm[0]{\operatorname{lcm}} \newcommand\set[1]{\left\{{#1}\right\}} \newcommand\ceil[1]{\left\lceil{#1}\right\rceil} \newcommand\floor[1]{\left\lfloor{#1}\right\rfloor} \newcommand\Vec[1]{\vec{\mathbf{#1}}} \newcommand\rank[0]{\text{rank}} \]

曾经写过一篇关于线代的博客，但是感觉问题很大，一是排版，二是专业术语不严谨，三是有许多错误，四是不是特别形象，于是就没管那篇了，重新写一篇，可能有采纳原来那一篇的部分内容，但同时，有一些是我在看完 \(\textsf{3B1B}\) 之后的一些笔记，可能后面还有会更新，不过现在就这么多了。总而言之，这篇博客是为了能够更形象地解释线代而作，同时方便自己的复习。可以两篇结合一起看。

注意，本篇文章的重点在与矩阵相关的理解上，类似 “向量是什么”“矩阵乘法是怎么运算的” 将会比较省略。另外，除了一章比较特别，其他章节除特殊交代外，都在分析方阵。

壹、矩阵、矩乘的本质

矩阵，可以看做是多个列向量拼起来，即对于方阵 \(A\)，它可以看成是

\[A=(\Vec {v_1}|\Vec{v_2}|\Vec{v_3}|\cdots|\Vec{v_n}) \]

其中 \(\Vec{v_i}\in \Bbb R^n\)，这就是一个 \(n\times n\) 的方阵。那么这一堆向量拼起来的这个矩阵有什么意义呢？我们不妨将每一个向量都看作是某一维的基底，也就是说，对于一个 \(n\) 维空间，它原本的基底拼起来的方阵是 \(I_n\)，即 \(n\) 维意义下的单位阵，因为第 \(i\) 维的基底就是该维的长度为 \(1\) 且指向正方向的向量。那么，对于 \(I_n\)，我们乘上一个 \(A\) 会发生什么？\(A\times I_n=A\)，即在 \(A\) 的作用之后，\(I_n\) 变成了 \(A\). 这个过程可以形象地理解为基底的变换，而其他的地方，因为他们的坐标没有变，但是由于基底变了，所以它们也有对应的变化。

也就是说，左乘一个方阵，实际上就是一个线性变换的作用，或者在空间上对基底的变换。

举个例子，就用上面的 \(A=(\Vec {v_1}|\Vec{v_2}|\Vec{v_3}|\cdots|\Vec{v_n})\)，我们考虑 \(\Vec w=(x_1,x_2,\cdots,x_n)\) 在经过 \(A\) 变换的结果：

\[A\Vec w=x_1\Vec {v_1}+x_2\Vec {v_2}+\cdots+x_n\Vec{v_n} \]
让我们继续吧！

现在考虑另外的问题，两个矩阵乘起来会得到什么？举个例子，假设我们有 \(A,B\) 两个 \(n\) 阶方阵，那么 \(A\times B\) 对的结果是什么？这太抽象了，我们不妨举个例子：现在有一个 \(\Vec v\in \Bbb R^n\)，结合前面所说，\(B\times \Vec v\) 将会得到 \(\Vec v\) 经过 \(B\) 变换之后的 \(n\) 阶向量，那么 \(A\times (B\times \Vec v)\) 就会得到 “\(\Vec v\) 先经过 \(B\) 变换再经过 \(A\) 变换” 的向量，根据矩阵的运算，\(A\times (B\times \Vec v)=(A\times B)\times \Vec v\)，那么我们可以很形象地理解矩阵乘法了：不同变换叠加的结果。为了更好地说明这个东西，下面再举一个例子：

试计算

\[\begin{bmatrix} 0 & -2 & 2 \\ 5 & 1 & 5 \\ 1 & 4 & -1 \end{bmatrix} \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} =\;? \]

当然你可以直接进行计算得到 \(3\times 3\) 的方阵，但是这里并不会说这种方法肯定不是我懒，我们介绍另一种方法。

我们已经知道了矩阵的乘法是变换的叠加，我们不妨将左边的矩阵看作 \(A\)，右边的矩阵看作 \(B\)，同时，设 \(B=(\Vec{v_1}|\Vec{v_2}|\Vec{v_3})\)，当经过 \(B\) 变换之后，原来 \(I_3\) 的基底将会变成 \(\hat i=\Vec{v_1},\hat j=\Vec{v_2},\hat k=\Vec{v_3}\)，再经过 \(A\) 变换，就是 \(\hat i,\hat j,\hat k\) 分别经过 \(A\) 变换之后再组成空间的基底，于是，上述矩乘得到的矩阵实际上就是：

\[(A\Vec{v_1}|A\Vec{v_2}|A\Vec{v_3}) \]

即三个基底分别变换之后再拼起来得到组合的效果。这样，我们不难得到最后的答案：（建议自己先算一算再看答案）

\[\begin{bmatrix} 6 & 6 & 6\\ 33 & 44 & 55\\ 6 & 10 & 14 \\ \end{bmatrix} \]

我绝对是用手算的！！！

贰、矩阵的行列式

我们已经知道矩阵实际上是对基底的变换了，而这种变换既有对于空间的拉伸，又有压缩，当然也存在不拉伸也不压缩的情况，仅仅只是旋转、剪切之类的操作。不过，为了描述一个变换对于空间的放缩情况，我们引入行列式这个概念。形象地，行列式形容的是原来一个单位(原来的大小为 \(1\))，经过矩阵变换之后的大小。举个例子（假设他们都是满秩的），一阶方阵，就是一个长度为 \(1\) 的线段经过拉伸或压缩之后的长度；二阶方阵，就是一个面积为 \(1\) 的正方形经过变换之后的面积；三阶方阵，就是一个体积为 \(1\) 的小立方体，在基底经过变换之后它的体积。我们将其记为一个方阵的行列式，即 \(\det A\).

不过，上述说的并不完全正确 —— 显然，大家一定也见过行列式为负的情况，这种情况的出现，是源于该变换对于基底的空间位置关系进行了颠覆，举个例子，一维矩阵，\(\det([4])=4\) 而 \(\det([-3])=-3\)，后者为负是因为它将 \(\hat i=[1]\) 变换为了 \(\hat i'=[-3]\)，它原来指向 \(x\) 正方向，但是变换之后的 \(\hat i'\) 竟然指向了负方向！这对于原来的数轴来说，就好像是将该数轴 “翻了一翻”；二维矩阵，本来的二维空间，\(\hat j\) 应该在 \(\hat i\) 的左边（用叉积说明方向），但是，对于某些变换来说，经过该变换之后 \(\hat j\) 在 \(\hat i\) 右边，这也是一种空间位置关系的颠覆，就好像是将这个平面翻转了一下；三维空间也是类似，本来 \(\hat i,\hat j,\hat k\) 应该满足叉积的右手定则，但是变换之后，你只能用左手来做 “右手”定则，这也说明该变换行列式为负。

另外还有一些情况 —— 行列式为 \(0\)，这显然不仅仅是一个变换了，因为，一个正常的变换，是不会将单位的大小变为 \(0\) 的，考虑什么时候一个单位的大小会变成 \(0\)：三维空间中，一个立方体体积变成 \(0\)，就相当于它变成了一个平面，一条线或一个点，也就是说，原本三维的概念，经过该变换之后变成了更低维度的东西。也就是说，虽然这个变换是三阶的，但是它的实质却只有二阶、一阶或零阶，可以形象地称其为维度的坍缩，这个时候我们称其为不满秩，这在下一章还会提到。

接下来，我们考虑说明一个东西：

\[\det(AB)=\det(A)\det(B) \]

两个变换叠加起来的放缩比率就相当于它们各自放缩比率之积。

如果真的想要求行列式，可以通过高斯消元法在 \(\mathcal O(n^3)\) 内求出，而不用按照定义在 \(\mathcal O(n!)\) 内求解它。

叁、矩阵的逆、列空间与核(零空间)

一般面对一个方程：

\[\begin{cases} 2x+5y+3z=-3 \\[2ex] 4x+8z=0 \\[2ex] 1x+3y=2 \end{cases} \]

我们当然可以将其看做三个涉及 \(x,y,z\) 的方程，当然，我们也可以看做是矩阵与向量作用的结果：

\[\begin{bmatrix} 2 & 5 & 3 \\ 4 & 0 & 8 \\ 1 & 3 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{bmatrix} -3 \\ 0 \\ 2 \end{bmatrix} \]

为了看做是方阵和向量之积，我们不得不添上几个 \(0\). 而它实际上就是：

\[A\Vec x=\Vec v \]

我们已知 \(A,\Vec v\)，想要求 \(\Vec x\).

形象上来说，我们想要求的 \(\Vec x\) 经过 \(A\) 变换之后得到了 \(\Vec v\)，反过来说，我们想要求一个 \(\Vec x\)，让它经过 \(A\) 变换之后能够得到 \(\Vec v\).

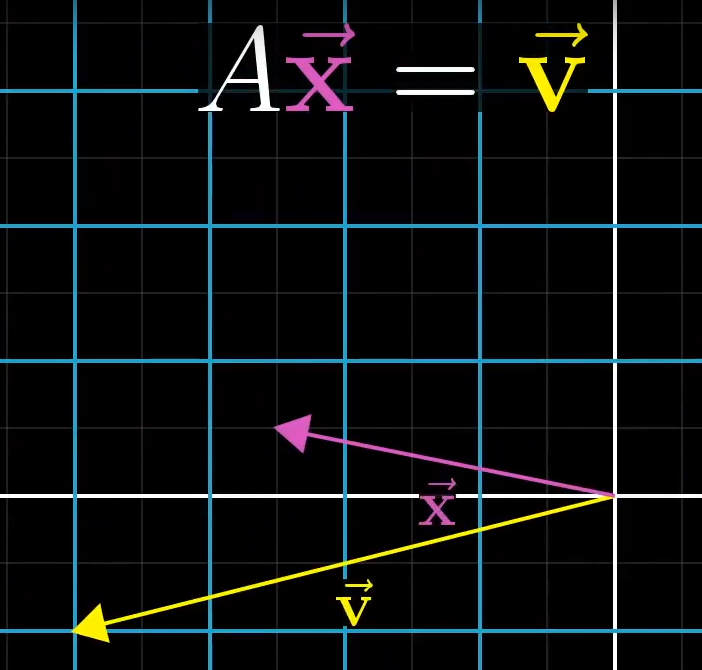
一个容易想到的思路是，我们找到一个 \(A^{-1}\)，它是 \(A\) 的逆矩阵（形象的理解，逆变换？），经过这个逆矩阵的变换，我们就可以求得 \(\Vec x=A^{-1}\Vec v\). 显然，这个逆变换 \(A^{-1}\) 一定满足 \(A^{-1}A=I\). 这个思路简洁明了，一步到位！

如果想要求 \(A^{-1}\)，可以通过高斯消元法将 \((A|I)\rightarrow (I|A^{-1})\)，这里不赘述。

不过这个方法要有一个前提 —— 我们一定可以找到 \(A\) 的逆矩阵，不过，也不是所有的 \(A\) 都有对应的逆矩阵的，对于某些 \(\det=0\) 的矩阵，我们无法找到这样一个矩阵，为什么？由前面所说，当 \(\det A=0\) 也就是它不满秩的时候，它的本质并非是将空间变换成以另一组向量为基底的空间，而是将该空间坍缩为一个更低维度的东西，举个例子：

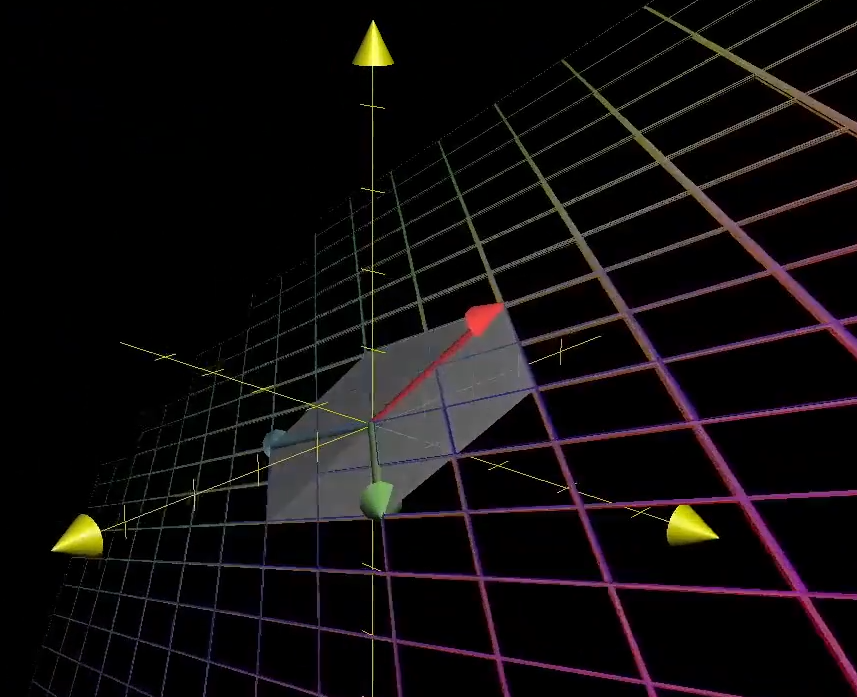
这个时候，三维的空间变成了二维的平面，由于逆变换实际上是将 \(\Vec v\) 变成我们想求的 \(\Vec x\)，但是现在，显然，可能存在多个 \(\Vec x\) 都可以经过该变换得到 \(\Vec v\)，做个类比：

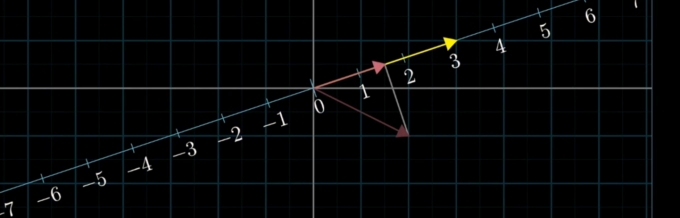
如果我们将向量沿一条直线作投影，显然会有多个向量在这条线上的投影都是一样的，而我们的变换只支持 “输入一个向量，输出一个向量”，它显然不可能做到 “解压缩”。不过，这也不意味着解一定不存在，下面这张截图很形象地说明了这个问题：

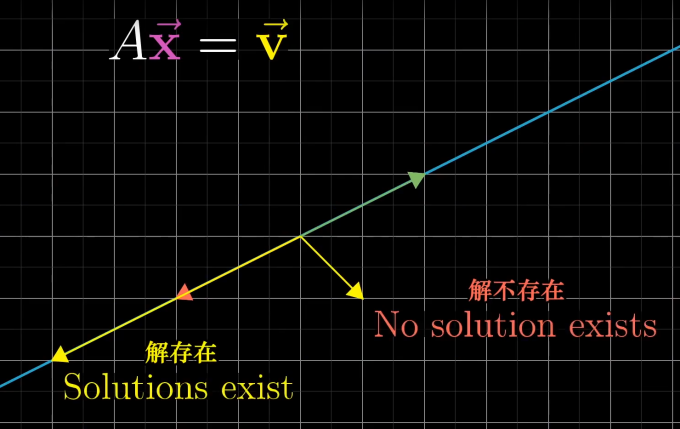
另外，同样 \(\det=0\)，有些情况下解存在的条件更加苛刻，比如，在上图中，最后空间被压缩成了一个点，而非一条直线，这个时候存在解当且仅当 \(\Vec v=(0,0)\)，而前者只要 \(\Vec v\) 在直线上即可。

那么我们如何区分这两种 \(\det=0\) 的情况？引入新的概念：秩（\(\rank\)），秩即形容了一个变换实质是几阶的，比如，上图中，将一个二维平面压缩成一维的直线，我们则说其秩为 \(1\). 秩其实代表着变换之后的空间维数，比如，一个二阶方阵，其秩最大为 \(2\)，这意味着基向量仍然能够张成二维的平面，不过，对于三阶方阵来说，秩为 \(2\) 意为着原本的空间经过变换之后坍缩为一个二维平面，但是相比于秩为 \(1\)，坍缩并非这么严重。

经过 \(A\) 变换之后的所有可能的输出向量组成的集合我们称其为该矩阵的 “列空间”，它其实就是方阵所有列向量所张成的空间，这样，更严谨地，矩阵的秩实际上就是该矩阵列空间的维数，当秩与列向量数量相同时，此时秩达到最大值，同时，我们称这种情况为 “满秩”。

对于一个满秩的矩阵 \(A\) 来说，唯一能够在变换之后还落在原点的，只有 \(\Vec 0\) 自身，而如果 \(A\) 不是满秩的，由于它将一个空间压缩到更低的维度，可能会有很多向量都落在原点，我们将这些向量构成的集合成为该矩阵的 “零空间” 或者 “核”，即 \(\ker(\mathscr A)=\set{\Vec x|\mathscr A\Vec x=\Vec 0}\).

肆、对于非方阵的特殊说明

非方阵其实很有意思，它可以将一个维度的一堆向量处理成为另外一个维度。直接说可能有点抽象，我们举个例子：

\[\begin{bmatrix} 2 & 0 \\ -1 & 1 \\ -2 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 3 & 3 \\ 2 & 4 & -1 \end{bmatrix} = \begin{bmatrix} 2 & 6 & 6 \\ 1 & 1 & -4 \\ 0 & -2 & -7 \end{bmatrix} \]

这就很有意思了，因为变换矩阵 \(A_{3\times 2}\) 将一堆二维向量变成了三维然后深藏功与名，这看上去是升维了，但是他们实际上还是拘泥于三维空间中由 \(\Vec {v_1}=(2,-1,-2)\) 与 \(\Vec {v_2}=(0,1,1)\) 张成的二维平面，所谓让你看到了高级的东西，但是却不给你，让你更绝望。

由上面这个例子，实际上我们已经可以总结出非方阵乘法各个参数的含义了：

对于变换矩阵：其行数为输出向量的维数，列数为接受向量的维数（原本空间的维数）；
对于被变换的向量矩阵：其行数为其原本所处空间的维数，列数为被变换的向量的数量；

值得注意的是，向量被变换之后已经不再处于原来的空间，因为空间的维数都不一样。我们另外举个例子，对于变换矩阵 \(A_{2\times 3}\) 来说，它接受原本维数为 \(3\) 的向量组，将他们映射为维数为 \(2\) 的向量组，或者将三维空间映射到二维空间；对于 \(A_{3\times 2}\) 来说，它接受 \(2\) 阶向量，将其映射到 \(3\) 阶向量，或者将二维空间映射到三维空间。

伍、To be continue......

标签：变换,text,矩阵,笔记,color,Vec,第二次,线代,向量
来源： https://www.cnblogs.com/Arextre/p/15848376.html