标签:NOI2012 int 题解 up son down facnt 环点 P2081
题目传送门 P2081
一些定义:
定义 \(fa_u\) 表示 \(u\) 的父亲,\(facnt_u\) 表示 \(u\) 的父节点个数(取值 \(1\) 或 \(2\)),\(son_u\) 表示 \(u\) 的儿子个数,\(ch_u\) 表示 \(u\) 的子节点,\(down_u\) 表示在以 \(1\) 为根的树中,从 \(u\) 出发第一步向下走的期望路径长度。\(up_u\) 表示从 \(u\) 出发第一步向上走的期望路径长度,\(w_{i,j}\) 表示 \(i\) 到 \(j\) 的边权。
那么对于每个点,其答案为 \(ans_u = \dfrac{1}{son_u + facnt_u} \times (son_u \times down_u + up_u \times facnt_u)\)。
最终答案即为 \(\dfrac{1}{n} \sum \limits_{i=1}^{n} ans_i\)。
50pts 部分分(图为一棵树):
此时 \(facnt_u = 1\)。因此 \(down\) 值不依赖 \(up\) 值。其推导较为简单:
\[down_u = \dfrac{1}{son_u} \sum \limits_{v \in ch_u} (down_v + w_{u,v}) \]而对于 \(up\) 值,需要依赖 \(down_{fa_u}\) 和 \(up_{fa_u}\)。此时我们第一步必须走到 \(fa_u\),并且再下一步不能走回 \(u\)。那么式子就推出来了:
\[up_u = w_{u,fa_u} + \dfrac{facnt_{fa_u} \times up_{fa_u} + son_{fa_u} \times down_{fa_u} - down_u - w_{u, fa_u}}{facnt_{fa_u} + son_{fa_u} - 1} \]这样我们就能得到 \(50 \tt pts\) 的好成绩了。
另外 50pts(图为一棵基环树):
我们将基环树看成一些树将跟连成环的结果。以下简称环上节点为 “环点”,其余为 “树点”。如图所示是一棵基环树,其中每个节点连向其父节点。
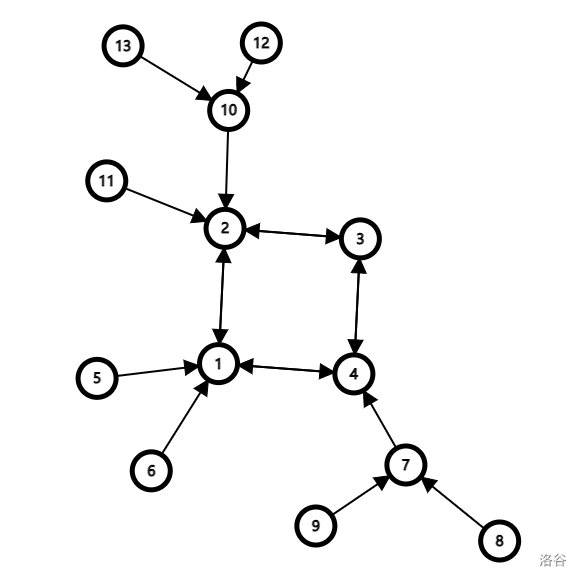
所有环点的 \(facnt=2\),树点的 \(facnt=1\)。
首先,根据定义,每个点的 \(down\) 值不变。而 \(up\) 值的求得就较为麻烦。
其次,考虑推导过程,每个树点的 \(up\) 值仍可以通过上述公式求得。而对于环点就比较麻烦,因为每一步我们可以选择走到一个环点,或走进当前环点的子树。
我们先通过遍历求出一些值(因为要进行后面的计算,同时我们需要按保证搜到环点的顺序,将这些环点顺序相连,正好是原图中的环):
- \(t\),表示环点的数量。
- \(dfn_u\),表示这个点是第几个被搜到的环点。
- \(id_i\),表示搜到的第 \(i\) 个环点的标号。
- \(disl_i, \, disr_i\),表示在环上,第 \(i\) 个被搜到的环点在环上的左右边权。
对于一个环点 \(u\),我们强制它逆时针在环上走,那么其 \(up\) 值公式为:
\[up_u = \sum _{i, v=id_i} p_i \times (\dfrac{son_v \times down_v}{son_v + 1} + w) \]其中 \(i\) 的取值分别为 \(dfn_u + 1, \, dfn_u + 2, \, \ldots t , \, 1, \, \ldots dfn_u - 1\)。虽然它看起来很奇怪,但确实是这个式子。
其中 \(p_i\) 表示走到这个环点的概率,由于我们限定第一步不进入子树,所以 \(p_{dfn_u \bmod t + 1}=1\)。对于每个环点,我们有几率进入它的子树,或者继续在环上走,所以 \(p_{i \bmod t + 1} = p_i \times \dfrac{1}{son_{id_i} + 1}\)。\(w\) 表示从上个环点走过来的边权。需要注意,如果按逆时针下一个环点已经走过了(即走了一圈),我们只能进入该点的子树。
上面规定的是第一步逆时针走的情况,顺时针的情况同理,两者的 \(up\) 值加起来 \(/2\) 即为最终的 \(up\) 值。或者直接将 \(p_{dfn_u \bmod t + 1}\) 设成 \(\dfrac12\) 也可以。
最后将每个树点的 \(up\) 值更新一遍即可。总复杂度为 \(O(n + k^2)\),\(k\) 为环点个数。
#define pii pair<int, int>
#define Ld double
#define pb push_back
#define mp make_pair
int n, m;
vector<pii > e[N];
namespace Tree {
Ld f[N], g[N];
void dfs(int u, int Fa) {
int nw = 0;
for(pii x : e[u]) {
int v = x.fi, w = x.se;
if(v == Fa) continue;
++nw;
dfs(v, u);
f[u] += f[v] + w;
}
if(nw) f[u] /= nw;
}
void dfs2(int u, int Fa) {
for(pii x : e[u]) {
int v = x.fi, w = x.se;
if(v == Fa) continue;
if(e[u].size() == 1) g[v] = w;
else g[v] = w + (g[u] + f[u] * (e[u].size() - (u != 1)) - f[v] - w) / (e[u].size() - 1);
dfs2(v, u);
}
}
void solve() {
dfs(1, 0);
dfs2(1, 0);
Ld ans = 0.0;
rep(i, 1, n) {
ans += (f[i] * (e[i].size() - (i != 1)) + g[i]) / e[i].size();
}
printf("%.5f\n", ans / n);
}
}
int t, pos, fl;
int facnt[N], son[N];
int id[N], dfn[N];
int disl[N], disr[N];
bool vis[N];
Ld f[N], g[N];
void dfs(int u, int Fa) {
vis[u] = 1;
for(pii x : e[u]) {
int v = x.fi;
if(v == Fa) continue;
if(vis[v]) {
pos = v;
return ;
}
dfs(v, u);
if(!fl && pos) {
if(pos == u) fl = 1;
return ;
}
if(fl) break;
}
vis[u] = 0;
}
void dfs2(int u, int Fa) {
id[++t] = u; dfn[u] = t;
for(pii x : e[u]) {
int v = x.fi, w = x.se;
if(dfn[v] || !vis[v] || v == Fa) continue;
disr[t] = disl[t + 1] = w;
dfs2(v, u);
}
}
void down(int u, int Fa) {
int cnt = 0;
for(pii x : e[u]) {
int v = x.fi, w = x.se;
if(vis[v] || v == Fa) continue;
++cnt;
down(v, u);
f[u] += f[v] + w;
}
if(son[u] = cnt) f[u] /= cnt;
}
void up(int u, int Fa) {
for(pii x : e[u]) {
int v = x.fi, w = x.se;
if(vis[v] || v == Fa) continue;
g[v] = w;
if(facnt[u] + son[u] - 1) g[v] += (g[u] * facnt[u] + f[u] * son[u] - f[v] - w) / (facnt[u] + son[u] - 1);
up(v, u);
}
}
int pre(int x) { return x == 1 ? t : x - 1; }
int nxt(int x) { return x == t ? 1 : x + 1; }
void solve() {
dfs(1, 0); // 将所有环点的 vis 标成 1
rep(i, 1, n) if(vis[i]) facnt[i] = 2; else facnt[i] = 1;
dfs2(pos, 0);
for(pii x : e[id[1]]) if(x.fi == id[t]) {
disl[1] = disr[t] = x.se;
break;
}
rep(i, 1, t) down(id[i], 0);
rep(i, 1, t) {
int u = id[i];
Ld p = 0.5;
int j = nxt(i); while(j != i) {
int v = id[j], w = disl[j];
if(nxt(j) == i) g[u] += p * (f[v] + w);
else g[u] += p * (f[v] * son[v] / (son[v] + 1) + w);
p /= son[v] + 1;
j = nxt(j);
}
p = 0.5;
j = pre(i); while(j != i) {
int v = id[j], w = disr[j];
if(pre(j) == i) g[u] += p * (f[v] + w);
else g[u] += p * (f[v] * son[v] / (son[v] + 1) + w);
p /= son[v] + 1;
j = pre(j);
}
}
rep(i, 1, t) up(id[i], 0);
Ld ans = 0.0;
rep(i, 1, n) ans += (facnt[i] * g[i] + son[i] * f[i]) / (son[i] + facnt[i]);
printf("%.5f\n", ans / n);
}
int main() {
qread(n, m);
rep(i, 1, m) {
int u, v, w;
qread(u, v, w);
e[u].pb(mp(v, w));
e[v].pb(mp(u, w));
}
if(m == n - 1) Tree::solve();
else solve(); // 基环树
return 0;
}
标签:NOI2012,int,题解,up,son,down,facnt,环点,P2081 来源: https://www.cnblogs.com/BreezeEnder/p/15803296.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
