标签:后效 include int dfrac ne cdot cases 动态 DP
\(\text{Description}\)
给定一个 \(n\) 个点 \(m\) 条边的无向连通图。从 \(1\) 号节点出发,每一步以相等的概率 随机 选择当前节点连出去的某条边,经过这条边走到下一个节点,获得等于这条边的编号的分数。到达 \(n\) 号顶点时结束。请对这 \(m\) 条边进行编号,使得获得的总分的期望值 最小。
\(\text{Solution}\)
考虑 \(\rm dp\),设 \(f_u\) 表示到达节点 \(u\) 的期望次数,\(g_i\) 表示经过边 \(i\) 的期望次数,\(d_u\) 表示节点 \(u\) 的度数。
对于图中的一条边 \((u,v)\),\(v\) 连出去 \(d_v\) 条边,只有一种情况会经过 \((u,v)\),所以有 \(\dfrac{f_v}{d_v}\) 种。
还要注意:
- 由于到 \(n\) 号点就停了,因此 \(n\) 号点对答案没有贡献,因此 \(u,v\) 都不能为 \(n\)。
- 一开始就在一号点,所以 \(f_1\) 初始值为 \(1\)。
所以有
\[f_u= \begin{cases} \sum\limits_{(u,v)\in E,v\ne n}\dfrac{f_v}{d_v}+1&u=1\\ \sum\limits_{(u,v)\in E,v\ne n}\dfrac{f_v}{d_v}&u\ne1,u\ne n \end{cases} \]对于边 \((u,v)\),有可能是从 \(u\) 过来的,也有可能是从 \(v\) 过来的。
即
\[g_{(u,v)}=\dfrac{f_u}{d_u}+\dfrac{f_v}{d_v}\quad u\ne n,v\ne n \]然后将 \(g\) 进行排序,贪心地选择即可。
但是我们发现一个问题,\(f_v\) 可以推到 \(f_u\),而更新后的 \(f_u\) 又能推到 \(f_v\),这样就没法处理了。我们把这种问题称为 有后效性 \(\rm dp\)。
怎么处理呢?
我们举个例子,假设是这样一张图:
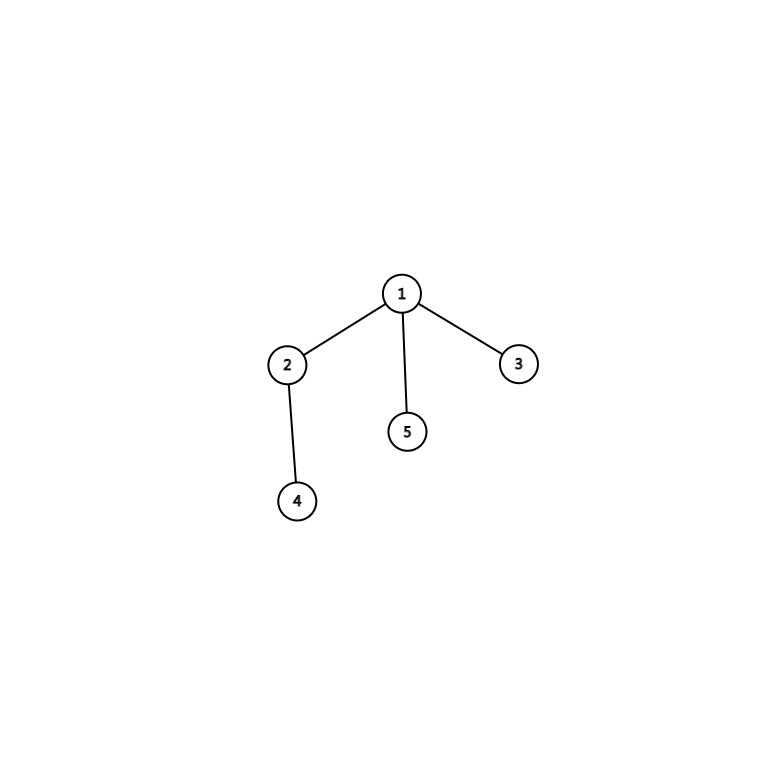
除 \(5\) 号点之外:
\[\begin{cases} f_1=\dfrac{f_2}{d_2}+\dfrac{f_3}{d_3}+1\\ f_2=\dfrac{f_1}{d_1}+\dfrac{f_4}{d_4}\\ f_3=\dfrac{f_1}{d_1}\\ f_4=\dfrac{f_2}{d_2} \end{cases} \]我们整理一下这个方程组:
\[\begin{cases} 1\cdot f_1-\dfrac{1}{d_2}\cdot f_2-\dfrac{1}{d_3}\cdot f_3+0\cdot f_4=1\\ -\dfrac{1}{d_1}\cdot f_1+1\cdot f_2+0\cdot f_3-\dfrac{1}{d_4}\cdot f_4=0\\ -\dfrac{1}{d_1}\cdot f_1+0\cdot f_2+1\cdot f_3+0\cdot f_4=0\\ 0\cdot f_1-\dfrac{1}{d_2}\cdot f_2+0\cdot f_3+1\cdot f_4=0 \end{cases} \]这就是一个 \((n-1)\) 元一次方程组,高斯(-约旦)消元即可。
时间复杂度 \(\mathcal{O}(n^3)\)。
\(\text{Code}\)
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
typedef double db;
using namespace std;
const int MAXN = 505;
const int MAXM = 125005;
int cnt;
int head[MAXN], st[MAXM], ed[MAXM], d[MAXN];
struct edge
{
int to, nxt;
}e[MAXM << 1];
void add(int u, int v)
{
e[++cnt] = edge{v, head[u]};
head[u] = cnt;
d[u]++;
}
int n, m;
db a[MAXN][MAXN];
db f[MAXN], g[MAXM];
void Gauss_Jordan()
{
for (int i = 1; i <= n; i++)
{
int mx = i;
for (int j = i + 1; j <= n; j++)
{
if (fabs(a[j][i]) > fabs(a[mx][i]))
{
mx = j;
}
}
if (mx != i)
{
swap(a[i], a[mx]);
}
for (int j = 1; j <= n; j++)
{
if (j != i)
{
db val = a[j][i] / a[i][i];
for (int k = i + 1; k <= n + 1; k++)
{
a[j][k] -= a[i][k] * val;
}
}
}
}
for (int i = 1; i <= n; i++)
{
f[i] = a[i][n + 1] / a[i][i];
}
}
bool cmp(double x, double y)
{
return x > y;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
{
scanf("%d%d", st + i, ed + i);
add(st[i], ed[i]);
add(ed[i], st[i]);
}
n--;
for (int u = 1; u <= n; u++)
{
a[u][u] = 1;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v != n + 1)
{
a[u][v] = -1.0 / d[v];
}
}
if (u == 1)
{
a[u][n + 1] = 1;
}
}
Gauss_Jordan();
for (int i = 1; i <= m; i++)
{
g[i] = f[st[i]] / d[st[i]] + f[ed[i]] / d[ed[i]];
}
sort(g + 1, g + m + 1, cmp);
db ans = 0;
for (int i = 1; i <= m; i++)
{
ans += i * g[i];
}
printf("%.3lf\n", ans);
return 0;
}
标签:后效,include,int,dfrac,ne,cdot,cases,动态,DP 来源: https://www.cnblogs.com/mangoworld/p/DP-with-Aftereffect.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
