标签:h2 题解 sum h1 NOI2016 h3 Longrightarrow 我们 P1721
蒟蒻的第一篇黑题题解,求过。
题意描述
这道题用简洁的话来说,就是:
给你 \(n\) 个数字,你可以让取其中任意若干个数字,每次操作,都会使所有取的数字变为取的数字的平均数,并且你最多只能进行 \(k\) 次操作,你要在这经过最多 \(k\) 次操作后使得给你的第一个数字变得最大。输出保留 \(p\) 位的第一个数字的最后状态。
贪心策略(非正解,有助后面做题)
我们暂且不研究这道题的正解是什么,我们先看看怎么样贪心能够使得第一个数字变得最大。
-
首先,比第一个数字小的我们一定不需要,它们会使第一个数字变得更低
-
第二,我们需要知道求平均数的顺序,我们设三个水量, \(h1,h2,h3(h1 <h2<h3)\) 。现在我们通过比较不同的顺序,看如何让 \(h1\) 变得最大。
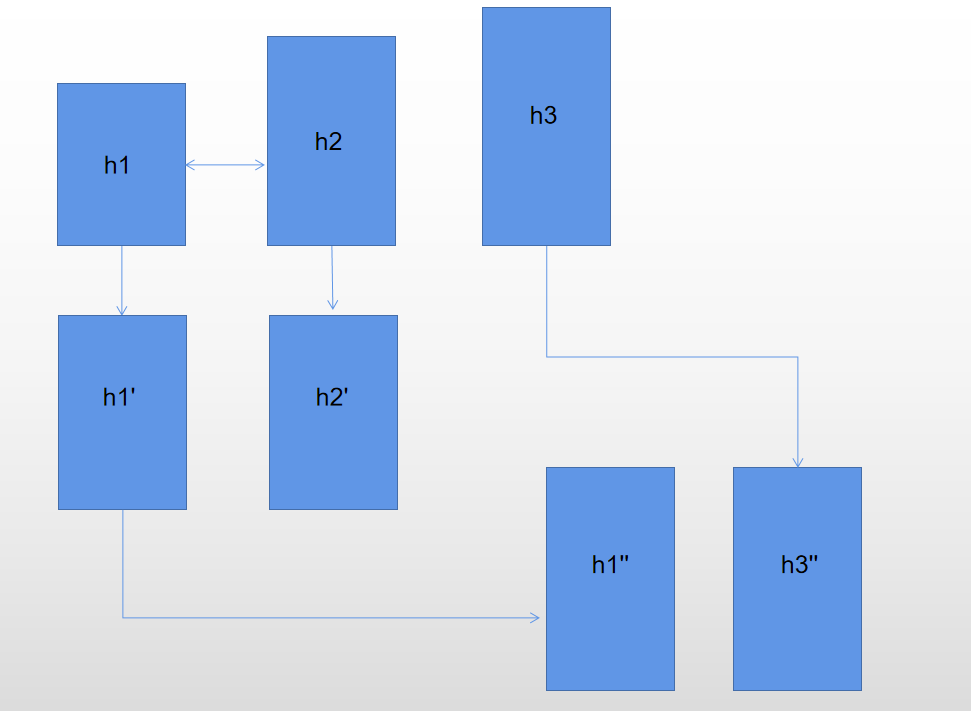
如图所示,已经是所有的顺序了:
- \(h1,h2,h3\) 同时求平均数。
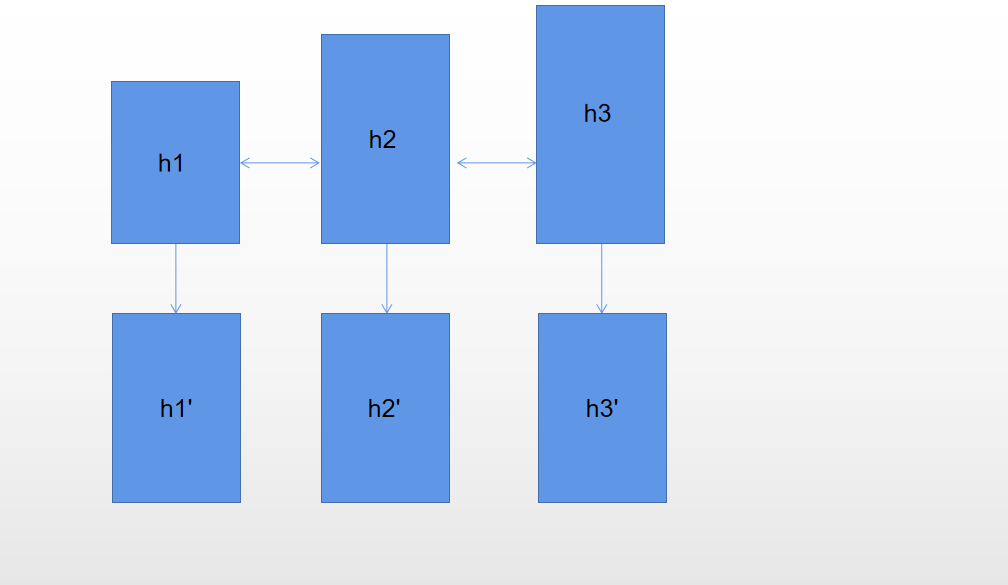
- \(h1\) 先和 \(h3\) 求平均数,然后和 \(h2\) 求平均数。
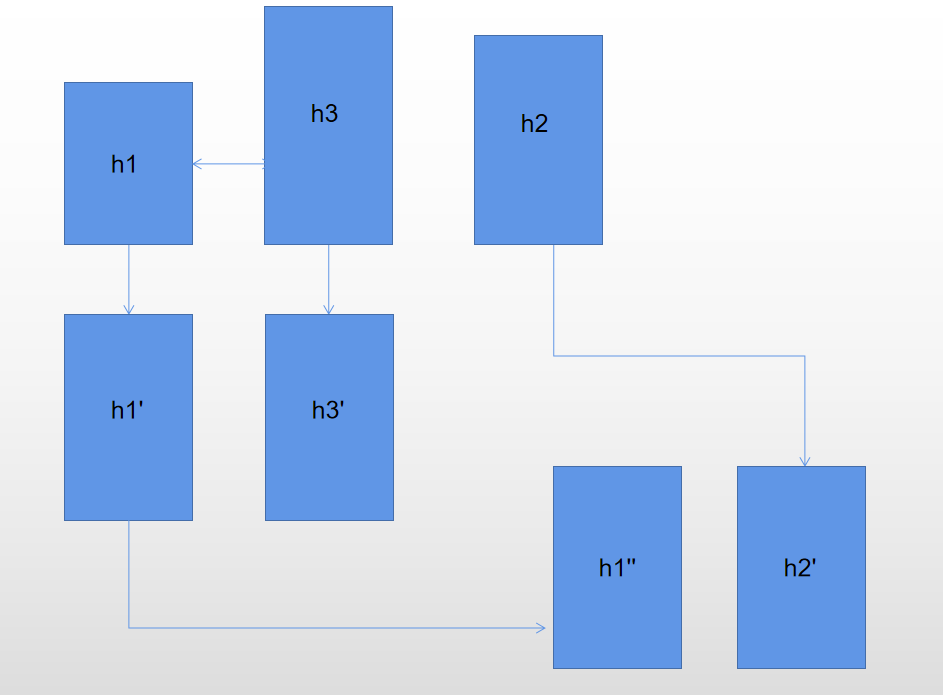
- \(h1\) 先和 \(h2\) 求平均数,然后和 \(h3\) 求平均数。
其实从图中就可以看出来,第三种方案最优。
我们再用数学的方法来比较这三个方案的优劣性。
-
第一种方案: \(h1=(h1+h2+h3)/3\)。
-
第二种方案: \(h1=((h1+h3)/2+h2)/2=(h1+h3)/4+h2/2\)。
-
第三种方案: \(h1=((h1+h2)/2+h3)/2=(h1+h2)/4+h3/2\)。
我们通过相减比较 \(h1\) 最后的大小:
- 第一种方案减去第三种方案:
第三种方案晋级。
- 第二种方案减去第三种方案:
第三种方案胜出。
总结策略
-
只考虑比第一个数大的数。
-
在一般情况下,一个一个操作(可能会超过 \(k\) 次,所以是在一般情况下)。
-
在一个一个操作时,从小到大操作。
斜率优化dp(正解)
由于可进行的操作次数是一定的,所以我们最后要解决的就是该在那一段区间进行操作。
首先将大于第一个数的数记录下来,排序并求出前缀和。
然后设计dp转移方程:
\(sum_i\) 为前 \(i\) 个数的前缀和(操作是赋值为平均数,并不会改变总数值,所以 \(sum_i\) 一直适用) 。
\(f_{i,j}\) 表示前面 \(i\) 个数操作了 \(j\) 次时第一个数的最大值。
得转移方程:
\[f_{i,j}=\max((f_{p,j-1}+sum_i-sum_{p-1})/(i-p+1)) \]code
for(int j=1;j<=k;j++)
for(int i=1;i<=n;i++)
for(int p=1;p<i;p++)
f[i][j]=max(f[i][j],(f[p][j-1]+sum[i]-sum[p-1])/(i-p+1));
但是这样的话,转移的时间复杂度为 \(O(n^2kp)\) ,(\(n\) 是数字个数, \(k\) 是操作次数,p为保留的精度)。
所以光是dp是不行的,我们要考虑优化dp。
我们观察这个状态转移方程:
\[(f_{p,j-1}+sum_i-sum_{p-1})/(i-p+1) \]\[\Longrightarrow (sum_i-(sum_{p-1}+f_{p,j-1}))/(i-(p-1)) \]由于 \(i\) 和 \(j\) 是循环中给出的,所以我们将 \(i\) 和 \(j\) 提出:
\[\Longrightarrow (sum_{p-1}-f_p)/(p-1) \]经过前后对比,我们发现,设当前点为 \((i,sum_i)\) ,转移点为 \((p-1,sum_{p-1}-f_p)\) ,其实就是斜率公式。
用斜率优化dp,还有很重要的条件是要有单调性。如图,这道题目的单调性也十分的明显,由于 \(1\le h_i \le 10^5\) ,也就意味着前缀和是单调上升的。
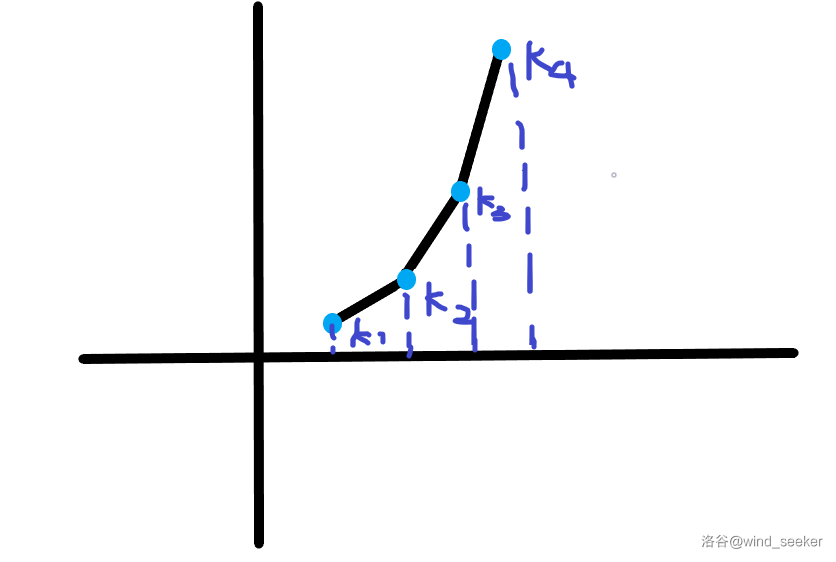
图画的不好,谅解。
那么我们要维护的就是图中的这一个凸包。
接下来我们考虑弹出队列的数会不会对后面的操作有影响:
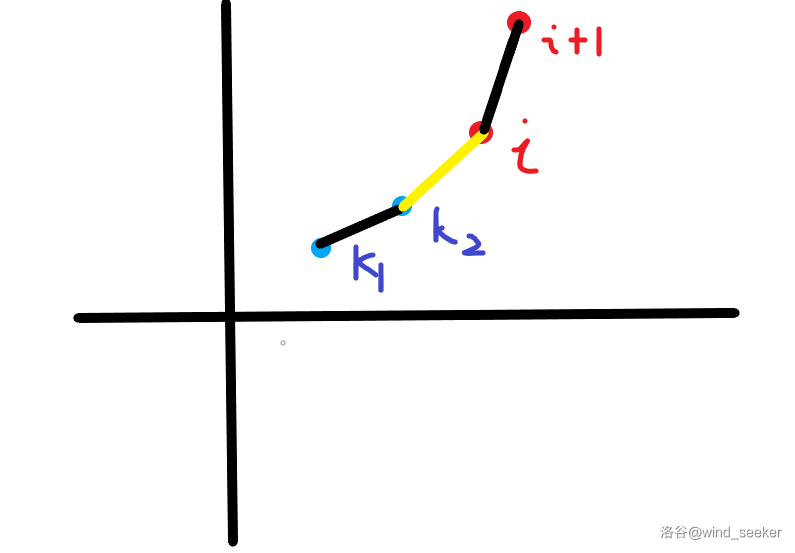
设当前位置为 \(i\) ,对于 \(i\) ,我们设 \(k_2\) 优于 \(k_1\) , 在这个情况下,我们可以得出:
\[(f_{k_1,j-1}+sum_i-sum_{k_1-1})/(i-k_1+1)<(f_{k_2,j-1}+sum_i-sum_{k_2-1})/(i-k_2+1) \]如果将 \(i+1\) 带入,结果为:
\[(f_{k_1,j-1}+sum_{i+1}-sum_{k_1-1})/(i+1-k_1+1)<(f_{k_2,j-1}+sum_{i+1}-sum_{k_2-1})/(i+1-k_2+1) \]比较两个式子,我们会发现,在 \(i+1\) 的情况下,如同 \(i\) 的情况相同, 原本优于 \(k_1\) 的 \(k_2\) 依然会比 \(k_2\) 更优,所以弹掉 \(k_1\) 并不会影响后面的操作。
code
for(int j=1;j<=k;j++)
{
int head=tail=1;
q[tail]=(node){1,sum[1]};
for(int i=2;i<=n;i++)
{
node x=(node){i,sum[i]};
while(head<tail&&slope(x,q[head])<slope(x,q[head+1]))head++;
f[i][j]=(f[q[head]][j-1]+sum[i]-sum[q[head]-1])/(i-q[head]+1);
while(head<tail&&slope(q[tail],q[tail-1])>slope(q[tail],i)) tail--;
q[++tail]=i;
}
}
此时我们已经将时间复杂度调小至 \(O(nkp)\) 。
\(n\le 8000\ \ k\le10^9\ \ p\le 3000\) 。
显然,我们还是不能过这道题目。
于是我们再次重审题目,看一下还有什么条件我们并没有用到。
Two thousands years later......
哦,我发,发现就怪了。
于是我参考了巨佬ljh2000的博客,终于发现了:\(h_i\) 互不相同。 那么那么就意味着......
好吧......
于是我又一次参考了巨佬ljh2000的博客,里面有两条十分重要的性质:
-
每一次操作的区间长度一定不比上一次操作的区间长度长!
-
在所有水量高度互不相同的情况下,长度大于1的区间仅有 \(O(\log{ \frac{nh}{H}})\) 个,其中 \(H=\min(h_i-h_{i-1})\) 。
首先我们证明第一个,十分简单。我们的目标是将 \(h_1\) 变得最大,而我们在一开始的时候对 \(h_i\) 进行了排序,所以越往后面, \(h_i\) 越大,越大的饼自然越要少与人分享,所以我们就会得出第一个结论。
至于第二个结论,我们只好根据众多大佬的指引,来到这里,深造一番。
Three thousands years later......
很好,没有任何的作用,看来只能等待某位大佬的指点,或者等本蒟蒻再深造几年再回答这个问题吧。
蒟蒻拙见,大佬勿喷。
标签:h2,题解,sum,h1,NOI2016,h3,Longrightarrow,我们,P1721 来源: https://www.cnblogs.com/windseekerblog/p/15255397.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。