在之前的内容中,我们完成了参数估计的步骤,今天起我们将进入假设检验部分,这部分内容可参照《数理统计学教程》(陈希孺、倪国熙)。由于本系列为我独自完成的,缺少审阅,如果有任何错误,欢迎在评论区中指出,谢谢!
目录Part 1:什么是假设检验
假设检验是一种统计推断方法,用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的。其步骤,其实就是提出一个假设,然后用抽样作为证据,判断这个假设是正确的或是错误的,这里判断的依据就称为该假设的一个检验。
假设检验在数理统计中有重要的用途,比如:橙子的平均重量是80斤,这就是一个假设。我们怎么才能知道它是对的还是错的?这需要我们对橙子总体进行抽样,然后对样本进行一定的处理,比如计算总体均值的区间估计,如果区间估计不包含80斤,就认为原假设不成立,便拒绝原假设。
当然,由于样本具有随机性,因此我们只是对该假设进行检验而不是证明,也就是说不论假设检验的结果是接受假设还是拒绝假设,都不能认为假设本身是正确的或是错误的。同时,假设的检验也不是唯一确定的,对任何假设都可以有无数种方案进行检验,比如上面的例子,\(95\%\)的区间估计是一种检验,\(99\%\)的区间估计也可以作为检验,\(90\%\)的当然也可以,只要事先确定了即可。
总之,要将实用问题转化为统计假设检验问题处理,一般需要经历以下几个步骤:
- 明确所要处理的问题,将其转化为二元问题,只能用“是”和“否”来回答。
- 设计适当的检验,规定假设的拒绝域,即拒绝假设时样本\(\boldsymbol{X}\)会落入的区域范围(当然也可以是统计量会落入的范围,这两个意思是一致的)。
- 抽取样本\(\boldsymbol{X}\)进行观测,计算需要的统计量的值。
- 根据样本的具体值作出接受假设或者否定假设的决定。
以下是假设检验问题的一些常用概念:
- 零假设即原假设,指的是进行统计检验时预先建立的假设,一般是希望证明其错误的假设,用字母\(H_0\)表示。这种区分方式比较玄乎。
- 备择假设指的是与原假设所相对立的假设,如果我们拒绝了原假设,就意味着需要接受备择假设。
- 拒绝域指的是我们会在什么时候拒绝原假设,也就是拒绝原假设时样本所属的集合,它是样本空间的一个子集。
在实际生活中,可以作出的假设是多种多样的,对不同的检验问题有不同的方法,我们接下来对其分别进行讨论。
Part 2:拟合优度检验
拟合优度检验指的是如下的检验问题——对于总体\(X\)和已知的分布\(F\),\(H_0\):\(X\)的分布为\(F\)。即用\(F(x)\)这个分布函数来拟合样本\(X_1,\cdots,X_n\),拟合的优良程度如何。
对于拟合优度检验,其检验思想是构造一个统计量\(D\),这个统计量刻画样本\(\boldsymbol{X}=(X_1,\cdots,X_n)\)与理论分布\(F\)的偏离程度,\(D\)越大代表理论分布\(F\)与样本表现出来的分布越不相符。由于在\(H_0\)成立也就是\(X\)的分布为\(F\)的条件下,\(D\)作为一个统计量具有确定的抽样分布,且这个统计量描述的是拟合的优良程度,自然\(D\)越小说明拟合得越好。因此,我们这样定义拟合优度:在获得\(\boldsymbol{X}\)的情况下计算出\(D\)的观测值\(D_0\),则拟合优度为
\[p(D_0)=\mathbb{P}(D\ge D_0|H_0). \]直观地想象拟合优度,由于作为偏离量\(D\)肯定是非负的,所以如果\(D_0\)越小,拟合优度就越大,同时这也代表着样本与理论程度的偏离小,所以拟合优度可以作为理论分布\(F\)是\(X\)的分布的可靠性度量。有了拟合优度之后,如果拟合优度太小,我们就会否定\(H_0\),否则接受\(H_0\),这需要一个阈值\(\alpha\)。常常取\(\alpha=0.05\),如果拟合优度小于\(\alpha\)就否定零假设,不过阈值的设定多少是有些主观的,因此客观的拟合优度往往比接受和否定的二元回答更有价值。
不过,我们现在还没有讨论偏离量具体应该如何定义,并且偏离量的定义方式也可以多种多样,因此我们接下来将分情况讨论拟合优度检验中,偏离统计量\(D\)的定义。
Section 1:离散型(分布已知)
如果\(X\)是离散型随机变量,则可以进一步区分为如下的两种:有限与可列。我们先讨论有限且分布已知的情况。现在,原假设是\(H_0\):\(X\)服从如下的分布:
\[F:\begin{pmatrix} a_1 & a_2 & \cdots & a_r \\ p_1 & p_2 & \cdots & p_r \end{pmatrix},\quad \sum_{i=1}^r p_i=1. \]适用于这种情况的检验是Pearson的\(\chi^2\)检验,这是我们所接触的第一个重要检验。以\(\nu_i\)记所有样本中取值为\(a_i\)的个数,称为观察频数,即
\[\nu_i=\#\{j|X_j=a_i\}. \]如果样本容量为\(n\),则理论上,应当有以下关系式:
\[p_i\approx \frac{\nu_i}{n},\quad \nu_i\approx np_i. \]称\(np_i\)为理论频数,如果\(H_0\)成立,则\(|np_i-\nu_i|\)对所有\(i\)都不应该过大,但又不能简单地取\((np_i-\nu_i)^2\),需要考虑权重问题。Pearson引进如下的统计量,常称为Pearson \(\chi^2\)统计量,为
\[K_n=\sum_{i=1}^r\frac{(np_i-\nu_i)^2}{np_i} \]这里,使用\(1/np_i\)作为权重的调整值,构造出检验统计量。使用这个权重的原因是Pearson证明的定理:在\(H_0\)成立的条件下,有\(K_n\stackrel{d}{\to }\chi^2_{r-1}\)。由此,如果由样本计算出\(K_n\)的观测值是\(k_0\),则拟合优度为
\[p(k_0)=\mathbb{P}(K_n\ge k_0|H_0)\approx\mathbb{P}(\tilde\chi^2_{r-1}\ge k_0), \]这里\(\tilde\chi^2_{r-1}\)指的是服从\(\chi^2_{r-1}\)分布的随机变量,这样拟合优度就可以用\(\chi^2\)分布的分位数表近似地计算。实际应用时,我们不一定需要这么精确的拟合优度,故只要查询阈值\(\alpha\)对应的分位数值\(\chi^2_{\alpha}(r-1)\),并比较它与\(k_0\)的大小即可,当\(\chi^2_{\alpha}(r-1)\le k_0\)时拒绝\(H_0\)。
这里,我们以书上的例题为例,介绍如何用R语言计算拟合优度。现在\(n=556\),
\[\begin{matrix} \nu_i \\ p_i \\ np_i \end{matrix}\begin{pmatrix} 315 & 108 & 101 & 32 \\ 9/16 & 3/16 & 3/16 & 1/16 \\ 312.75 & 104.25 & 104.25 & 34.75 \end{pmatrix} \]调用自定义函数
pearson.chi2(obersved, prob),代码见附录。这个函数将返回一个列表,其中我们所需要的是\(\chi^2\)统计量的值和拟合优度,故进行如下调用:> observed <- c(315, 108, 101, 32) > prob <- c(9, 3, 3, 1) > pearson.chi2(observed, prob) Pearson chi2 test The value of K: 0.470024 p-value: 0.9254259 Accept.这里,
The value of K是卡方统计量的值,p-value是拟合优度。如果需要进一步使用返回值的其他信息,这个函数会返回一个列表。
如果\(X\)是可列的离散随机变量,则需要对观测进行分组,将其划分为\(r\)个区间,这样就将其转化为有限的情形。具体地,分组需要让每一个组内的理论频数和观察频数都不小于5为宜。
Section 2:连续型(分布已知)
如果理论分布是一个已知的连续型分布,虽然分组法依然可以解决(具体可以参考书本内容),但是不论如何取分组间隔,都多少遗漏了信息。对于连续型分布的验证,使用柯尔莫哥洛夫检验(柯氏检验)更为合适。为此,我们需要先介绍经验分布函数。
经验分布函数是一个结合了分布函数的单调、非降、左连续特色的函数,不同的是它可以由样本计算得出。简而言之,经验分布函数就是将经验分布函数中,\(F(x)=\mathbb{P}(X< x)\)的概率变成频率。
注意,苏中根《概率论》中,分布函数的定义是右连续的即\(F(x)=\mathbb{P}(X\le x)\),而这里经验分布函数的定义却是左连续的。不过,将分布函数定义成左连续或是右连续并不影响使用,我们不妨就遵照左连续的定义。
设\(X_1,\cdots,X_n\)是\(X\sim F\)中抽取的简单随机样本,次序统计量为\((X_{(1)},\cdots,X_{(n)})\),则\(\forall x\),定义以下函数为经验分布函数:
\[F_n(x)=\left\{\begin{array}l 0,& x\le X_{(1)};\\ \frac{k}{n},& X_{(k)}<x\le X_{(k+1)},k=1,\cdots,n-1;\\ 1,& X_{(n)}<x. \end{array} \right. \]R语言的plot.ecdf函数可以绘制经验分布函数。下面给出一个指数分布的经验分布函数与实际分布函数的示意图:
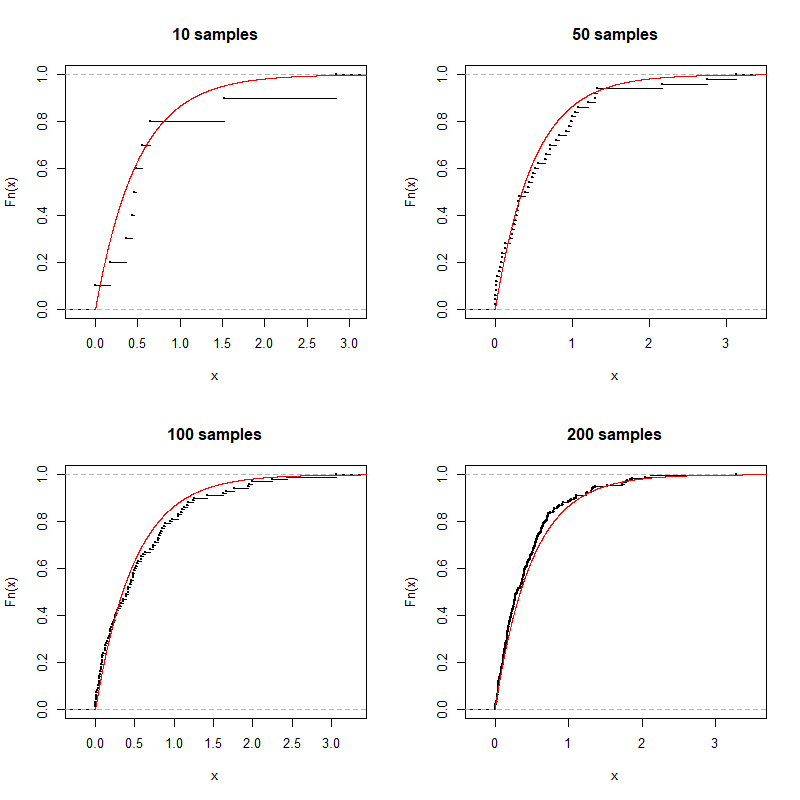
对于每一个确定的\(x\),易知
\[F_n(x)=\frac{1}{n}\sum_{i=1}^n I_{-\infty<X_{i}<x}, \]而
\[\mathbb{P}(I_{-\infty<X_i<x}=1)=\mathbb{P}(X_i<x)=F(x), \]所以\(F_n(x)\)是一个有限取值的离散型随机变量,有
\[nF_n(x)\sim B(n,F(x)). \]这样,有\(\mathbb{E}[F_n(x)]=F(x)\),由强大数定律,\(\forall x\in \mathbb{R}\),\(F_n(x)\stackrel{\mathrm{a.s.}}\to F(x)\),即经验分布函数逐点收敛于分布函数。更进一步,如果记\(D_n\)为\(F_n(x)\)与\(F(x)\)的最大偏离,即
\[D_n=\sup_{x\in\mathbb{R}}|F_n(x)-F(x)|, \]则格里汶科定理保证了
\[\mathbb{P}\left(\lim_{n\to \infty}D_n=0 \right)=1. \]柯尔莫哥洛夫进一步地证明了以下的结论:
\[\lim_{n\to \infty}\mathbb{P}\left(D_n\le \frac{\lambda}{\sqrt{n}} \right)=K(\lambda),\\ K(\lambda)=\sum_{k=-\infty}^\infty (-1)^ke^{-2k^2\lambda^2},\lambda>0. \]注意这个\(D_n\),它显然可以用来描述经验分布与理论分布的偏离程度,因此我们显然可以用它入手来完善拟合优度检验理论。柯氏检验就是建立在经验分布函数基础上的,此时我们取理论分布为\(F\)计算\(D_n=\sup\limits_{x\in\mathbb{R}}|F_n(x)-F(x)|\),再根据确定的阈值\(\alpha\),让\(K(\lambda)=\alpha\)找到合适的\(\lambda\),则检验的临界值就是
\[D_{n,\alpha}=\frac{\lambda}{\sqrt{n}}=\frac{K^{-1}(1-\alpha)}{\sqrt{n}}. \]由于经验分布函数是阶梯型的,真实的分布函数又是单调的,所以\(D_n\)必定出在各个\(X_i\)的观测值处,具体地有
\[D_n=\max\left\{\left|F_0(x_{(i)})-\frac{i-1}{n} \right|,\left|F_0(x_{(i)})-\frac{i}{n} \right|,\quad \forall i=1,2,\cdots,n \right\}. \]R语言提供了Kolmogorov-Smirnov检验函数
ks.test(x, y),其中斯米尔诺夫检验适用于检验两组样本是否同分布的。以书上例题为例,可以如下调用:> num <- c(0.034, 0.437, 0.863, 0.964, 0.366, 0.469, 0.637, 0.632, 0.804, 0.261) # 书本误将0.437打成了0.0437,可以在底下的计算表中看出 > ks.test(num, qunif) One-sample Kolmogorov-Smirnov test data: num D = 0.166, p-value = 0.9052 alternative hypothesis: two-sided如果我们需要验证的已知分布,则
ks.test的第二个参数直接用分布的名称即可(采用默认参数,如果不是默认的\(U(0,1)\)或者\(N(0,1)\)则对样本数据作变换)。
今天,我们介绍了拟合优度检验的部分内容,由于篇幅所限,拟合优度检验的剩余部分将放到下一篇文章中介绍。关于Pearson \(\chi^2\)独立性检验的函数,我将其放到附录中,在使用时可以用source()函数访问,也可以直接将函数复制运行。
附录:
1、经验分布函数绘制
rm(list=ls())
dev.off()
opar <- par(no.readonly = T)
x <- seq(0,6,0.001)
y <- pexp(x, rate = 2)
par(mfrow = c(2,2))
plot.ecdf(rexp(10, 2), cex=0.1, main = "10 samples")
lines(x, y, col='red')
plot.ecdf(rexp(50, 2), cex=0.1, main = "50 samples")
lines(x, y, col='red')
plot.ecdf(rexp(100, 2), cex=0.1, main = "100 samples")
lines(x, y, col='red')
plot.ecdf(rexp(200, 2), cex=0.1, main = "200 samples")
lines(x, y, col='red')
2、自定义函数pearson.chi2()
pearson.chi2 <- function(x, p, alpha=0.05){
# x是实际频数,p是概率列表,alpha是阈值
rt <- list()
r <- length(x) # 可能出现的情况
p <- p / sum(p) # 归一化概率列表
n <- sum(x) # 总数
np <- n*p # 理论频数
rt$observed <- x
rt$dim <- r
rt$total.observed <- n
rt$prob <- p
rt$expect <- np
K <- 0
for (i in 1:r){
K = K + (np[i]-x[i])^2/np[i]
}
rt$pearson.chi2 <- K
p.value <- 1 - pchisq(K, df=r-1)
rt$p.value <- p.value
cat("\n\tPearson chi2 test\n\n")
cat("The value of K: ", K, "\n")
cat("p-value: ", p.value, "\n")
if (p.value > alpha){
cat("Accept.\n")
}
else{
cat("Reject.\n")
}
lst <- rt
}
标签:函数,假设,假设检验,优度,检验,分布,拟合,14 来源: https://www.cnblogs.com/jy333/p/statistical_14.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
