标签:mathbb frac 分布 样本 Beta 数理统计 beta 参数估计 Delta
接下来我们就对除了正态分布以外的常用参数分布族进行参数估计,具体对连续型分布有指数分布、均匀分布,对离散型分布有二项分布、泊松分布几何分布。
今天的主要内容是均匀分布的参数估计,内容比较简单,读者应尝试一边阅读,一边独立推导出本文的结论。由于本系列为我独自完成的,缺少审阅,如果有任何错误,欢迎在评论区中指出,谢谢!
目录Part 1:均匀分布的参数估计
一般说来,离散分布似乎比连续分布好讨论一些,但是对于参数估计问题,由于我们此前接触的正态分布是连续的,具有样本联合密度函数,所以大家也许对具有联合密度的分布会更熟悉。
对于均匀分布\(U(a,b)\),它有两个参数:下界和上界。为找到其充分统计量,需写出其样本联合密度,不妨先写出总体密度:
\[f_1(x)=\frac{1}{b-a}I_{a<x<b}, \]注意,要讨论均匀分布的密度,示性函数是必不可少的(不过在讨论分布函数时倒往往不用示性函数,希望你在实践中能知道为什么),否则会给结论的得出造成障碍。接下来是联合密度函数:
\[\begin{aligned} f(\boldsymbol{x})&=\frac{1}{(b-a)^n}I_{a<x_1<b}\cdots I_{a<x_n<b}\\ &=\frac{1}{(b-a)^n}I_{a<x_{(1)}<x_{(n)}<b}. \end{aligned} \]这里的关键技巧在于,把\(n\)个条件\(I_{a<x_i<b}\)整合成
\[I_{a<x_{(1)}<x_{(n)}<b}, \]这样就将\(n\)个样本压缩成两个关键的统计量:\(X_{(1)},X_{(n)}\),从而由因子分解定理,\((X_{(1)},X_{(n)})\)是\((a,b)\)的充分统计量,因此对\(a,b\)的估计,就是对\((X_{(1)},X_{(n)})\)作调整,使之成为\(a,b\)的估计量。
对均匀分布的表示方法还有一种:\(U(a,a+r)\),\(r>0\)。这种表示往往不关心\(a\)的值,而只是关心均匀分布的区间有多广。这种形式下,样本的联合密度函数是
\[f(\boldsymbol{x})=\frac{1}{r^n}I_{x_{(n)}-x_{(1)}<r}\cdot I_{a<x_{(1)}}. \]由因子分解定理,此时样本极差:\(R=R(\boldsymbol{X})=X_{(n)}-X_{(1)}\)是\(r\)的充分统计量。
现在是无偏调整环节,为了使参数估计量是无偏的,就得求\(X_{(1)}\)和\(X_{(n)}\)的期望,因此不可避免地需要讨论它们的分布。对于一般的次序统计量我们还没有求过分布,但是样本最小、最大值的分布,在概率论里已经讨论过(不过当时可能大家都没记吧),只要用逻辑关系就可以得出。
不过,次序统计量终究是比较重要的,它的分布值得单独说一下。因此,我们先讨论一般情况下次序统计量的分布,再具体到均匀分布,得出\(a,b\)的无偏估计量。
Part 2:次序统计量
先给出次序统计量的定义,虽然大家可能都已经很明确了:如果\(X_1,\cdots,X_n\)是来自总体\(X\sim F\)的简单随机样本,按大小顺序排列为\(X_{(1)}\le \cdots \le X_{(n)}\)后,\((X_{(1)},\cdots,X_{(n)})\)为样本的次序统计量。
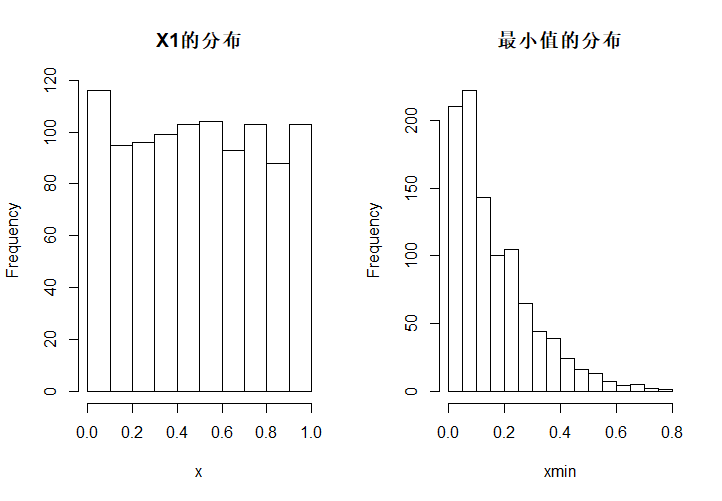
必须明白的是,次序统计量也是统计量,而且是一个\(n\)维随机向量,只是我们一般研究的是其中一两个向量的边际分布。并且,\(X_{(1)}\)和\(X_1\)的分布肯定是不同的,这是因为加上了次序性以后,随机向量内部出现了结构,从而改变了分布。下面是对\(U(0,1)\)中抽样的1000次模拟,每一次模拟样本容量为5,两图分别是\(X_1\)的分布与\(X_{(1)}\)的分布。
rm(list = ls())
x <- c()
xmin <- c()
for (i in 1:1000){
u01 <- runif(5)
x[i] <- u01[1]
xmin[i] <- sort(u01)[1]
}
split.screen(c(1, 2))
screen(1)
hist(x, main = "X1的分布")
screen(2)
hist(xmin, main = "最小值的分布")
现在,对一般的分布函数\(F\),\(X_1,\cdots,X_n\stackrel{\mathrm{i.i.d.}}\sim F\),我们来探讨次序统计量\(X_{(k)}\)的密度\((1\le k\le n)\),记此密度为\(p_{k}(x)\)。求次序统计量的密度函数,最好采用一种微元的处理方式,即
\[p_k(x)=F_k'(x)=\lim_{\Delta x\to 0}\frac{F_k(x+\Delta x)-F_k(x)}{\Delta x}, \]单独分析极限以内的部分,\(F_k(x+\Delta x)-F_k(x)\)意味着\(X_{(k)}\)落在\(x\)和\(x+\Delta x\)之间,这相当于\(n\)个样本中,有\(k-1\)个落在\(x\)之前,\(n-k\)个落在\(x+\Delta x\)之后,剩下一个刚好落在区间内。由于各个样本之间出现概率是均等的,所以考虑到轮换性,可以考虑\(X_1,\cdots,X_{k-1}<x\),\(X_{k+1},\cdots,X_n>x+\Delta x\),恰好有\(X_k\in[x,x+\Delta x]\),再乘上\(C_{n}^{k-1}C_{n-k+1}^{n-k}\)即可。所以
\[\quad F_k(x+\Delta x)-F_k(x)=C_{n}^{k-1}C_{n-k+1}^1[F(x)]^{k-1}[1-F(x+\Delta x)]^{n-k}[F(x+\Delta x)-F(x)], \]而恰好
\[\lim_{\Delta x\to 0}\frac{F(x+\Delta x)-F(x)}{\Delta x}=p(x), \]所以代回\(p_k(x)\),有
\[p_k(x)=n!p(x)\cdot\frac{[F(x)]^{k-1}}{(k-1)!}\frac{[1-F(x)]^{n-k}}{(n-k)!}. \]这就得到了\(X_{(k)}\)的密度。特别代入\(k=1\)和\(k=n\)时,有
\[p_1(x)=n[1-F(x)]^{n-1}p(x)\Rightarrow F_1(x)=1-[1-F(x)]^n;\\ p_n(x)=n[F(x)]^{n-1}p(x)\Rightarrow F_n(x)=[F(x)]^n. \]之前我们在讨论最小值、最大值的分布时,总是从逻辑关系先得出分布函数,再求导得出密度函数;这里的思路却刚好相反,先导出密度函数,再积分得到分布函数。
采用这种微元的思想,导出任意个次序统计量的联合分布也很简单。考虑两个次序统计量\((X_{(k)},X_{(l)})\)的分布且假定\(k\le l\),则同理有
\[p_{k,l}(x,y)=\lim_{\Delta x\to 0 \\ \Delta y\to 0}\frac{F(x+\Delta x,y+\Delta y)-F(x,y)}{\Delta x\Delta y}. \]分子也可以看成有\(k-1\)个位于\(x\)之前,\(l-k-1\)个位于\(x,y\)之间,\(n-l\)个位于\(y\)之后,但这里还要注意\(x<y\)。所以通过相似的计算,可以得出
\[p_{k,l}(x,y)=n!p(x)p(y)\cdot\frac{[F(x)]^{k-1}}{(k-1)!}\cdot\frac{[F(y)-F(x)]^{l-k-1}}{(l-k-1)!}\cdot \frac{[1-F(y)]^{n-k}}{(n-k)!}I_{x<y}. \]注意到次序统计量密度函数的规律性的话,应该很容易背出它的形式,而不需要每次都推导一遍。
应当注意到,将样本的取值范围通过\(x,y,\cdots\)分成若干截,按照次序统计量的特性将样本分配到每个点、每个区间上,每个区间的样本数量对应着当前段取值的概率,也对应着样本在区间内部的轮换可能性。
本段只是次序统计量记忆的一个技巧,具体细节可以由读者自己完善。
一般研究到两个样本的边际分布就完全够用了,具体的数字特征还有赖于具体的分布函数来计算,不过既然我们研究的是均匀分布,就用均匀分布来讨论一下好了。
Part 3:均匀分布次序统计量与\(\beta\)分布
我们不需要讨论任何均匀分布\(U(a,b)\),只需要讨论其中的代表:\(U(0,1)\),这是因为如果\(U\sim U(0,1)\),则\((b-a)U+a\sim U(a,b)\)(请读者自己尝试证明这一点,不要想得太复杂哦)。
\(U(0,1)\)的分布函数\(F(x)\)和密度函数\(p(x)\)分别是
\[p(x)=I_{0<x<1},\\ F(x)=x,\quad (0\le x\le 1). \]所以\(X_{(k)}\)的密度函数代入计算,是
\[p_k(x)=n!\frac{x^{k-1}}{(k-1)!}\frac{(1-x)^{n-k}}{(n-k)!}I_{0<x<1}=\frac{\Gamma(n+1)}{\Gamma(k)\Gamma(n-k+1)}x^{k-1}(1-x)^{n-k+1-1}I_{0<x<1}. \]前面那个分数,恰好是欧拉函数中的\(\beta\)函数的倒数:
\[\beta(k,n-k+1)=\frac{\Gamma(k)\Gamma(n-k+1)}{\Gamma(n+1)}, \]因此有
\[p_k(x)=\frac{1}{\beta(k,n-k+1)}x^{k-1}(1-x)^{n-k+1-1}I_{0<x<1}. \]暂时你可能不会对这个形式的密度函数有很大的触动,但是以后我们会经常跟这个密度函数打交道,我们称之为\(\beta\)分布。形式上,\(\beta\)分布的支撑集是\((0,1)\),即\(\beta\)分布只会在\((0,1)\)上取值,并且忽略其正则化常数后,剩下的部分呈现的形式是\(x^{a-1}(1-x)^{b-1}\),对这部分积分,可以得到
\[\int_{0}^{1}x^{a-1}(1-x)^{b-1}\mathrm{d}x=\beta(a,b). \]现在,我们可以给出\(\beta\)分布的定义了:称\(X\sim \beta(a,b)\),如果\(X\)具有如下的密度函数:
\[p(x)=\frac{1}{\beta(a,b)}x^{a-1}(1-x)^{b-1}. \]可以看到,\(\beta\)分布最重要的特征就是,其核(去掉正则化系数的剩余部分)是\(x\)和\((1-x)\)的任意次方。
同时,我们可以得出一个重要结论:若\(X_{(k)}\)是\(U(0,1)\)的第\(k\)个次序统计量,则
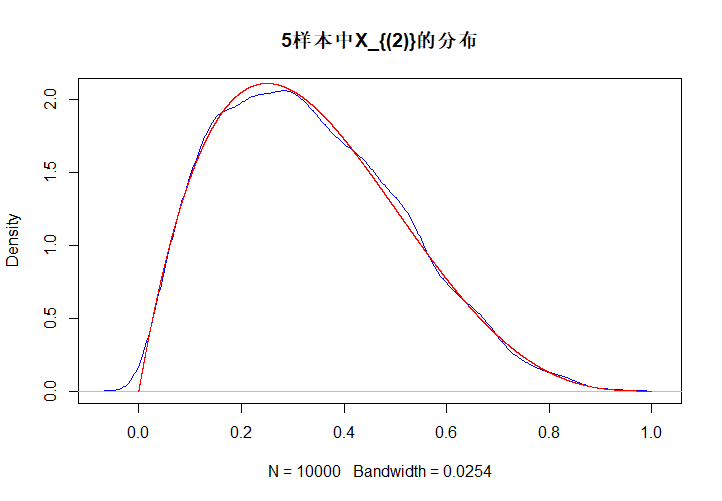
\[X_{(k)}\sim \beta(k, n-k+1). \]下面是对\(U(0,1)\)抽取5个样本时,\(X_{(2)}\)的分布模拟,蓝色的是样本分布,红色的是理论分布。
rm(list = ls())
xmin <- c()
for (i in 1:10000){
u01 <- runif(5)
xmin[i] <- sort(u01)[2]
}
plot(density(xmin), main = "5样本中X_{(2)}的分布", col = 'blue') # 绘制核密度函数
y <- seq(0, 1, 0.0001)
beta24 <- dbeta(y, 2, 4) # 绘制Beta(2, 4)的密度函数
lines(y, beta24, col = 'red')
现讨论\(\beta\)分布的数字特征,以便以后对\(X_{(1)},X_{(n)}\)作无偏调整。由于\(\beta\)分布核的特殊形式,其期望和方差都很好计算。设\(X\sim \beta(a,b)\),则
\[\begin{aligned} \mathbb{E}(X)&=\int_0^1 \frac{1}{\beta(a,b)}x^a(1-x)^{b-1}\mathrm{d}x\\ &=\frac{\beta(a+1,b)}{\beta(a,b)}\int_0^1\frac{1}{\beta(a+1,b)}x^{a+1-1}(1-x)^{b-1}\mathrm{d}x\\ &=\frac{\Gamma(a+1)\Gamma(b)/\Gamma(a+b+1)}{\Gamma(a)\Gamma(b)/\Gamma(a+b)}\\ &=\frac{a}{a+b}. \end{aligned} \]这里第三个等号成立是因为积分内部是\(\beta(a+1,b)\)的密度函数,其完全积分为1。同理方差为
\[\begin{aligned} \mathbb{E}(X^2)&=\int_0^1\frac{1}{\beta(a,b)}x^{a+1}(1-x)^{b-1}\mathrm{d}x\\ &=\frac{\beta(a+2,b)}{\beta(a,b)}\\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\frac{\Gamma(a+2)\Gamma(b)}{\Gamma(a+b+2)}\\ &=\frac{(a+1)a}{(a+b+1)(a+b)},\\ \mathbb{D}(X)&=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2\\ &=\frac{a(a+1)}{(a+b+1)(a+b)}-\frac{a^2}{(a+b)^2}\\ &=\frac{a(a+1)(a+b)-a^2(a+b+1)}{(a+b+1)(a+b)^2}\\ &=\frac{ab}{(a+b+1)(a+b)}. \end{aligned} \]具体到\(X_{(k)}\sim \beta(k,n-k+1)\),有
\[\mathbb{E}(X_{(k)})=\frac{k}{n+1},\quad \mathbb{D}(X_{(k)})=\frac{k(n-k+1)}{(n+1)(n+2)}\to 0. \]特别对\(X_{(1)},X_{(k)}\),有
\[\mathbb{E}(X_{(1)})=\frac{1}{n+1},\quad \mathbb{E}(X_{(k)})=\frac{n}{n+1}. \]对于\(U(a,b)\),其样本最小值和最大值记作\(Y_{(1)}\)和\(Y_{(n)}\),则有
\[Y_{(k)}=(b-a)X_{(k)}+a,\\ \mathbb{E}(Y_{(1)})=\frac{an+b}{n+1}\to a,\\ \mathbb{E}(Y_{(n)})=\frac{bn+a}{n+1}\to b. \]所以对均匀分布而言,样本最小值、样本最大值分别是下界、上界的渐进无偏估计。由于其方差趋近于0,也容易证明,样本最小值、样本最大值是弱相合估计。
现在讨论总体极差的估计,在上面的讨论中已经知道总体极差应当用样本极差来估计。对于\(X\sim U(0,1)\),令\(R=X_{(n)}-X_{(1)}\),为讨论其分布,需要作一个简单变换:
\[U=X_{(1)},\\ V=X_{(n)}-X_{(1)}. \]这个变换的Jacobi行列式绝对值为\(|J|=1\),所以
\[\begin{aligned} p(u,v)&=p_{1,n}(x_{(1)},x_{(n)}) \\ &=n(n-1)(x_{(n)}-x_{(1)})^{n-2}I_{0<x_{(1)}<x_{(n)}<1} \\ &=n(n-1)v^{n-2}I_{0<u<u+v<1}. \end{aligned} \]欲求\(V\)的边际分布,考虑积分范围是\(u\in(0,1-v)\),所以
\[p_v(v)=I_{0<v<1}\int_0^{1-v} n(n-1)v^{n-2}\mathrm{d}u=n(n-1)(1-v)v^{n-2}I_{0<v<1}. \]这就是\(R\)的密度函数:
\[p_R(x)=n(n-1)(1-x)x^{n-2}I_{0<x<1}, \]求其期望,有
\[\begin{aligned} \mathbb{E}(R)&=n(n-1)\int_0^1 x(x^{n-2}-x^{n-1})\mathrm{d}x\\ &=n(n-1)\left(\frac{1}{n}-\frac{1}{n+1} \right)\\ &=\frac{n-1}{n+1}. \end{aligned} \]而\(Y_{(n)}-Y_{(1)}=(a+r-a)(X_{(n)}-X_{(1)})=rR\),所以
\[\mathbb{E}(Y_{(n)}-Y_{(1)})=\frac{r(n-1)}{n+1}\to r, \]故样本极差为\(r\)的渐进无偏估计,可以修正为无偏估计:
\[R_n^*=\frac{n+1}{n-1}r. \]对下表中每个\(n\)进行10000次\(U(3,8)\)模拟,得到样本极差的均值如下:
\(n\) 5 10 15 20 30 40 50 100 200 \(\mathrm{mean}(R_n)\) 3.3475 4.0927 4.3769 4.5258 4.6764 4.7538 4.8055 4.9024 4.9505 \(\mathbb{E}(R_n)\) 3.3333 4.0909 4.3750 4.5238 4.6774 4.7561 4.8039 4.9010 4.9502 rm(list = ls()) nlst <- c(5, 10, 15, 20, 30, 40, 50, 100, 200) meanlst <- c() for (j in 1:9){ R <- c() for (i in 1:10000){ minmax <- range(runif(nlst[j], 3, 8)) R[i] <- minmax[2] - minmax[1] } meanlst[j] <- mean(R) } meanlst
最后,我们绕了一个大圈,还没有说今天的结论呢。既然今天我们的主要目标是对\(U(a,b)\)进行参数估计,我们有以下的结论:
- 对于均匀分布\(U(a,b)\),\((X_{(1)},X_{(n)})\)是\((a,b)\)的充分统计量。
- \(X_{(1)}\)是\(a\)的渐进无偏估计,\(X_{(n)}\)是\(b\)的渐进无偏估计。总有\(\mathbb{E}(X_{(1)})>a,\mathbb{E}(X_{(n)})<b\)。
- 样本极差是总体极差的渐进无偏估计,总有\(\mathbb{E}(R)<b-a\)。
这些估计量的有偏性来源往往很直观,因为不管如何抽取,样本都不可能比\(a\)小,比\(b\)大,所以无论抽取次数多少,\(X_{(1)}\)的支撑总在\(a\)的右侧,\(X_{(n)}\)的支撑总在\(b\)的左侧,所以期望必定不是\(a,b\)。极差也同理,不管抽取次数多少,期望总是小于实际极差的。
思考:能不能利用\((X_{(1)},X_{(n)})\)给出\(a,b\)的无偏估计量?
此外,我们今天还认识了一个非常重要的分布:\(\beta\)分布。如果\(X\sim \beta(a,b)\),则其密度函数为
\[p_X(x)=\frac{1}{\beta(a,b)}x^{a-1}(1-x)^{b-1}I_{0<x<1}. \]它的特点是:支撑集为\((0,1)\),核为\(x^k(1-x)^l\)。特别地,我们指出如果\(X_1,\cdots,X_n\)是来自\(U(0,1)\)的简单随机样本,则
\[X_{(k)}\sim \beta(k,n-k+1). \]今天我们花了大量的篇幅讨论均匀分布的点估计问题,明天我们就转向另一个连续分布:指数分布。同时,明天我们将看到另一个欧拉函数导出的分布:\(\Gamma\)分布。
标签:mathbb,frac,分布,样本,Beta,数理统计,beta,参数估计,Delta 来源: https://www.cnblogs.com/jy333/p/14357993.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
