标签:山河 那么 限制 int AHOI2022 重整 考虑 prod 我们
今年的独立命题除了福建都很一可赛艇啊!
首先有个经典结论是,如果选出的子集 \(S\) 合法,那么 \(\forall i, \sum_{j \in S,j \leq i} j \geq i\)。
那么可以得到一个 \(O(n^2)\) 的 DP。定义 \(dp_{i,j}\) 为在前 \(i\) 个数中,可以构出 \([1,j]\) 内的所有数(第二维与 \(n\) 取最小值),直接转移即可。
陷入困境。一方面这个 DP 的形式不好优化,另一方面容易发现这个 DP 的劣势在于第二维进行了压缩,我们无法得知准确的信息。
那么考虑算不合法的方案数。我们在每一个方案中第一个无法被表示的位置 \(i+1\) 计数。容易发现此时小于等于 \(i\) 的数的和就是 \(i\)。
那么定义 \(f_i\) 为集合 \(\{1,2,\cdots,i\}\) 有多少子集使得和为 \(i\),且可以表示 \([1,i]\) 内的所有数。遗憾的是在这里我们陷入困境,一方面是直接朴素 DP 和上面的形式毛区别也没有,另一方面可以表示 \([1,i]\) 内的所有数这个限制非常的离谱。
但是,注意到和为 \(i\) 这个限制,并且选出的数都不相同,容易发现我们选出来的数是 \(O(\sqrt n)\) 级别的,并且避免了信息的压缩。那我们转换计数视角,下面给出一个实例:
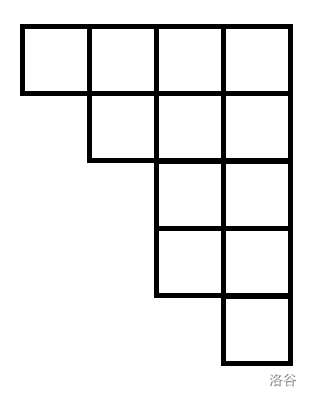
容易发现我们选择了 \(S=\{1,2,4,5\}\),和为 \(12\)。其中大小不同的行数量级别为 \(O(\sqrt{12})\)。(也可以按整数拆分选择的不同数个数这个角度来考虑。)
那么考虑我们之前 DP 的实质,我们是每次加入一列。那么这里我们按行来考虑。发现这个图有如下特点:
- 行的最大值是 \(O(\sqrt n)\) 的,已经强调了很多次了;
- 上面的行大小都不小于下面的行;
- 如果大小为 \(i\) 的行出现了,那么大小在 \([1,i-1]\) 内的行都出现了。
根据实际意义容易发现到上面的结论。
注意到我们直接计算 \(f_i\) 仍然困难,因为可以表示 \([1,i]\) 内的所有数这个限制确实比较难处理。我们考虑容斥,先算出一个不考虑这个限制的 \(f_i\)。
如何算这个不带限制的 \(f_i\) 呢?容易发现每个大小的行可以出现任意次,类似于完全背包,区别在于带了类似「如果要选 \(i\),必须先选 \([1,i-1]\) 内的每个数至少一次」限制。那么我们考虑从大的数选起,每次枚举到 \(i\) 的时候为了保证更上面的方案是合法的,我们先选择一个 \(i\),然后再更新。
// 此时 f[0] 不等于 1
for(int i=n;i;--i)
{
if(LL(i)*(i+1)/2>n) continue;
// 从大的开始选,要保证 i 一定要被选到。从小的开始选的话可能会缺。考虑实际意义,因为 1~p 都要被选到才合法。
for(int j=n;j>=i;--j) f[j]=f[j-i];
// 我先单选个 i,保证之前选择的方案合法
++f[i];
for(int j=i;j<=n;++j) add(f[j],f[j-i]);
// 做完全背包。
}
f[0]=1;
那么对每个 \(i\) 考虑容斥掉不合法的方案数,得到正确的 \(f_i\)。
先考虑对 \(i\) 有贡献的 \(j\)。首先为了方便计数,并且为了满足定义,显然我们后来选的最小的数为 \(j+2\)(因为我们要满足选之后,\(j+1\) 是最小的不能被构出的数,并且和为 \(i\))。那么不难发现对 \(i\) 有贡献的 \(j\),满足 \(2j+2 \leq i\)。
注意到这个点,我们在处理 \(f_{1 \sim n}\) 的时候,可以先处理 \(f_{1 \sim \frac{n}{2}}\),然后继续处理后面的东西。
那么我们已经知道了前面一半的 \(f\),要求后面一半。
这个时候继续考虑加入每一行之类的想法就非常的没有前途(主要是我没找到)。注意到我们现在要的是,通过选择 \([j+2,i]\) 里面的数,使得和为 \(i-j\)。我们考虑划分数相关的想法。
假设没有选择的数限制(但是还是有选择的数不能重复的限制),不妨写作生成函数的形式:
\[F(x) = \prod_{i=1}^{∞} (1+x^i) \]再来考虑这个东西的意义……我们按上面的方格图的形式把它排好,然后第 \(i\) 列从下往上删去 \(i\) 个方格(可以发现不会发现没东西删的情况,因为第 \(i\) 列的格子数显然不小于 \(i\)),容易发现上面的行仍然大于等于下面的行,当然这没有什么用。现在减去这个之后形式变成了类似于整数拆分的形式,并且有限制选择的最大的数。
那么,枚举选择的集合的大小:
\[F(x) = \sum_{i=1}^∞ x^{\frac{i(i+1)}{2}} \prod_{j=0}^{i} \dfrac{1}{1-x^j} \]不难发现 \([x^{i-j}]F(x)\) 就是没有限制的情况下我们要的结果。
但是现在带限制。首先上界我们不用管,可以考虑对 \(x^n\) 之类的东西取模;主要的是下界 \(j+2\),在我们上面设计的模型下相当于每一列多了 \(j+1\) 个格子,只跟 \(j+1\) 有关系。
记 \(F_p(x)\) 为下界为 \(p+1\) 时的生成函数,那么有:
\[\begin{aligned} F_p(x) &= \prod_{i=p+1}^∞ (1+x^i) \\ &= \sum_{i=1}^∞ x^{\frac{i(i+1)}{2}} x^{ip} \prod_{j=0}^i \dfrac{1}{1-x^j} \end{aligned} \]再记生成函数 \(G(x)\) 表示一下需要减去的贡献:
\[G(x) = \sum_{j=0}^{n} f_j x^j F_{j+1}(x) \]把 \(G\) 求出来,更新 \(f\) 的后一半即可。
注意到计算 \(F_p(x)\) 的过程中,\(i\) 的上界为 \(O(\sqrt n)\),后面 \(\prod\) 内的内容是完全背包(感觉可以和一开始的做法产生有机联系,可惜我没有发现),可以做到 \(O(n \sqrt n)\)。
可以采用其他的手段得到更优的做法。
Key observation: 正难则反,视角转换,生成函数。
int f[500005],g[500005];
void Solve(int n)
{
if(n<=1) return ;
Solve(n/2);
for(int i=1;i<=n;++i) g[i]=0;
for(int i=n;i;--i)
{
if(LL(i)*(i+1)/2>n) continue;
for(int j=n;j>=i;--j) g[j]=g[j-i];
for(int j=0,t=j+(j+2)*i;t<=n;++j,t=j+(j+2)*i) add(g[t],f[j]);
for(int j=i;j<=n;++j) add(g[j],g[j-i]);
}
for(int i=n/2+1;i<=n;++i) sub(f[i],g[i]);
}
int main(){
int n=read();
MOD=read();
for(int i=n;i;--i)
{
if(LL(i)*(i+1)/2>n) continue;
for(int j=n;j>=i;--j) f[j]=f[j-i];
++f[i];
for(int j=i;j<=n;++j) add(f[j],f[j-i]);
}
f[0]=1;
Solve(n);
int ans=1;
for(int i=0;i<n;++i) add(ans,ans),sub(ans,f[i]);
write(ans);
return 0;
}
标签:山河,那么,限制,int,AHOI2022,重整,考虑,prod,我们 来源: https://www.cnblogs.com/amagaisite/p/16283512.html
本站声明: 1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享; 2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关; 3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关; 4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除; 5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。
